Im vorherigen Artikel „Excel-Funktion lernen: 5 Möglichkeiten, die LOOKUP-Funktion zu verwenden“ haben wir die 5 Möglichkeiten kennengelernt, die LOOKUP-Funktion zu verwenden. Heute werde ich die beiden Teile erklären Nachdem Sie die Prinzipien der Methode verstanden haben, lesen Sie noch einmal das gestrige Tutorial. Ich glaube, Sie werden ein anderes Verständnis von LOOKUP haben.

Im vorherigen Artikel haben wir verschiedene Routinen der LOOKUP-Funktion kennengelernt und auch oft erwähnt, dass die Suche der LOOKUP-Funktion auf der Dichotomiemethode basiert. Lassen Sie uns heute darüber sprechen Diese Frage.
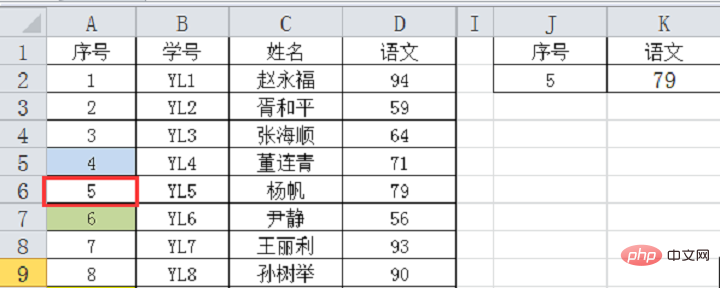
Nehmen wir noch das Beispiel von gestern: Suchen Sie nach Ergebnissen nach Seriennummer, die Seriennummern sind in aufsteigender Reihenfolge und das Ergebnis der Formel =LOOKUP(J2,A2:D19) ist korrekt.

1. Prinzip der binären Suche
Bei der binären Suche werden die Daten im Suchbereich entsprechend der Anzahl in zwei Teile geteilt, um Daten an der mittleren Position und den mittleren Wert zu finden und diese dann zu verwenden Unsere Suche Vergleichen Sie den Wert mit dem Mittelwert. Wenn der Mittelwert gleich dem Suchwert ist, wird das Ergebnis direkt erhalten. Wenn der Mittelwert kleiner als der Suchwert ist, wird der binäre Suchvergleich nach unten fortgesetzt (d. h. die binäre Suche wird in der unteren Hälfte fortgesetzt). Daten ohne den Mittelwert). Wenn der Zwischenwert größer als der Suchwert ist, wird der binäre Suchvergleich nach oben fortgesetzt (d. h. die binäre Suche wird in der oberen Hälfte der Daten ohne den Zwischenwert fortgesetzt). Wenn nach der Dichotomisierung zu den letzten Daten keine Daten gefunden werden, die dem Suchwert entsprechen: Wenn die letzten Daten kleiner als der Suchwert sind, verwenden Sie die Position der letzten Daten, um den Ergebniswert zu erhalten Suchwert, dann nach oben suchen Die Daten, deren Position den letzten Daten am nächsten liegt, sind kleiner oder gleich dem Suchwert, und dann wird das Ergebnis basierend auf der Position dieser Daten erhalten.
Dies ist nur eine Erklärung und ich denke, viele Freunde werden verwirrt sein. Nehmen wir das obige Beispiel, um im Detail zu sehen, wie man die chinesische Punktzahl von 79 bis zur Seriennummer 5 findet.
Erster Vergleich: Es gibt 18 Daten im Suchbereich A2 ~ A19, und die mittlere Position ist 18 ÷ 2 = 9, d. h. der mittlere Wert ist 9 in Zelle A10. Offensichtlich ist der Suchwert 5 kleiner als 9, also fahren Sie mit der Suche nach oben in A2~A9 fort.
Tipp: Wenn die Anzahl der Daten im Suchbereich eine ungerade Zahl ist, ist die mittlere Position (Zahl + 1) ÷ 2. Wenn es beispielsweise Zeile 11 gibt, ist die mittlere Position (11+1) ÷ 2 = 6; wenn die Anzahl der Daten eine gerade Zahl ist, ist die mittlere Position (Zahl) ÷ 2.

Zweiter Vergleich: Es gibt nur 8 Daten, die mittlere Position ist 8 ÷ 2 = 4, der mittlere Wert ist 4 in Zelle A5, der Suchwert 5 ist größer als 4, also suchen Sie weiter nach unten in A6 ~ A9. Beachten Sie, dass es derzeit nur vier Nummern darunter gibt und die Daten unter 9 bei der ersten Suche direkt ausgeschlossen werden.

Der dritte Vergleich: 4 Daten, der mittlere Wert ist 6 von A7, der Suchwert 5 ist kleiner als 6, also suchen Sie nach oben. Zu diesem Zeitpunkt gibt es nur noch einen Datenwert, 5 in Zelle A6, der mit dem Suchwert übereinstimmt, sodass die Daten 79 in Spalte D erhalten werden, die 5 entsprechen.

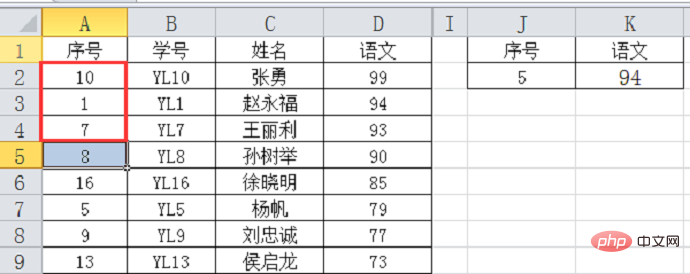
Es ist sehr schwierig, die Dichotomie anhand eines solchen Beispiels zu verstehen. Schauen wir uns ein anderes Beispiel an. Ordnen Sie die Daten in der obigen Tabelle in absteigender Reihenfolge der Ergebnisse an oder suchen Sie nach chinesischen Ergebnissen anhand der Seriennummer 5. Die Formel muss nicht geändert werden. Da die Reihenfolge der Seriennummernspalte nicht in aufsteigender Reihenfolge ist, tritt ein Fehler auf. Die tatsächliche Zahl ist 79 und die Formel ergibt 94. Was ist los? Betrachten wir es durch Dichotomie.
Die erste Suche: Der mittlere Wert (die 9. Daten) ist 18, der Suchwert 5 ist kleiner als 18, also suchen Sie nach oben in A2~A9;

Die zweite Suche: die obigen 8 Daten, die Mitte Der Wert (die 4. Daten) ist 8, der Suchwert 5 ist kleiner als 8, suchen Sie weiter nach oben in A2 ~ A4;

Die dritte Suche: die oben genannten 3 Daten, der mittlere Wert ist 1, die Suche Der Wert 5 ist größer als 1. Suchen Sie nach unten:

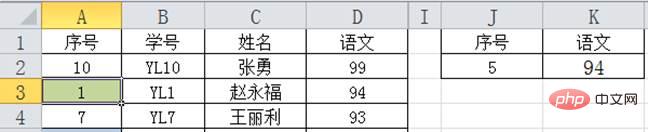
Die vierte Suche: Jetzt gibt es nur noch ein Datum 7 in Zelle A4 und der Suchwert 5 ist kleiner als 7. Verwenden Sie also 7 als Referenz und suchen Sie eine Position am nächsten an 7, und der Wert ist kleiner als 5 oder Die Daten gleich 5 sind 1 in Zelle A3, und der daraus erhaltene entsprechende chinesische Wert ist 94.
Durch diese beiden Beispiele denke ich, dass jeder ein gewisses Verständnis für die Dichotomie haben sollte. In Bezug auf dieses Prinzip gibt es nur einen Satz in der Funktionsbeschreibung:

In praktischen Anwendungen müssen wir uns keine Gedanken darüber machen, was die Dichotomie ist, was die mittlere Position ist, ob wir nach unten oder nach oben schauen sollen, das ist die ganze Arbeit der Funktion, wir müssen uns nur an eines erinnern: das Die Daten müssen in aufsteigender Reihenfolge angeordnet werden. Wenn sie nicht in aufsteigender Reihenfolge angeordnet werden können, folgen Sie der genauen Suchroutine von LOOKUP, um die Formel zu entwerfen.
2. LOOKUP implementiert Datenrundung
Das ist die Einführung in das Prinzip der Dichotomie. Als nächstes müssen wir die beiden zuvor verbleibenden Probleme lösen.
In dem Artikel vom 12. Mai haben wir LOOKUP verwendet, um ein Rundungsproblem zu lösen. Infolgedessen hinterließen alle Nachrichten mit der Bitte um eine Erklärung:

Was ist also diese Formel, die bei allen eine hitzige Diskussion ausgelöst hat? Schauen Sie sich das Bild unten an:

Es stellt sich heraus, dass diese Formel die LOOKUP-Funktion verwendet, um alle Zahlen unterhalb der Hundertstelstelle abzurunden und so eine Perzentilrundung zu erreichen.
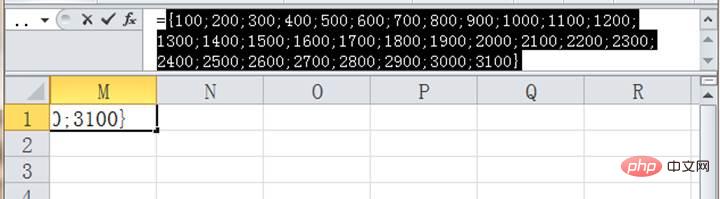
Nachdem wir das Prinzip der Dichotomie verstanden haben, ist es an der Zeit, dass LOOKUP es allen erklärt. Erklären Sie zunächst den Teil ROW (A:A)*100. Es erhält eigentlich nur eine Reihe von Zahlen. Um es allen verständlich zu machen, verkleinern wir den Bereich von A:A. Zur Erklärung verwenden wir =ROW(A1:A31)*100:

Obwohl Sie in der Zelle nur eine 100 sehen können, gibt es sie Eigentlich 31 Zahlen, können wir die Funktionstaste f9 verwenden, um den spezifischen Inhalt anzuzeigen:

ROW-Funktion wird verwendet, um die Zeilennummer der Zelle zu erhalten. ROW(A1:A31)*100 wird mit den Zeilennummern von multipliziert Zellen A1 bis A31. Mit 100 erhalten wir einen auf Hunderterstellen gerundeten Datensatz {100;200;300;...3000;3100}.
Dann kamen LOOKUP auf die Bühne. Es sucht nach A1 in dem oben erhaltenen Array, das auf Hunderterstellen gerundet wurde. Da das Array in aufsteigender Reihenfolge angeordnet ist, besteht der Kern der Suche nach A1 darin, den Maximalwert im Array zu finden, der kleiner oder gleich A1 ist.
Am Beispiel von 2517,32 ist nur der Maximalwert kleiner als 2500, das Ergebnis ist also 2500. Interessierte Freunde können es nach dem Dichotomieprinzip selbst ausprobieren, um zu sehen, ob es richtig ist.
Das Gleiche gilt für die Suche nach anderen Zahlen. Der Grund, warum diese Formel clever ist, liegt darin, dass sie ein Rundungsproblem in ein Problem des Findens von Referenzen verwandelt. Es ist wirklich wunderbar!
3. LOOKUP für die Datenextraktion
Wir haben LOOKUP erneut für die Datenextraktion verwendet, also hatten wir einen Termin mit 5000 Wörtern:

Was ist dieses Mal das Problem? Die ursprüngliche Frage extrahiert die Studentennummer wie im Bild gezeigt:

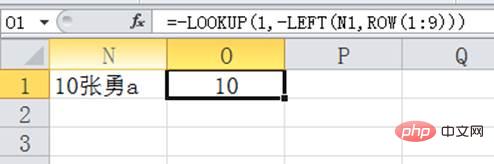
Lassen Sie uns zur Erklärung die ersten Daten im Bild oben verwenden. Geben Sie „10 Zhang Yong a“ in Zelle N1 ein und geben Sie dann die Formel =-LOOKUP(1,-LEFT(N1,ROW(1:9))) in Zelle O1 ein, um die Schülernummer zu extrahieren.

Ist LOOKUP nicht eine Referenzfunktion? Wie kann es wieder Zahlen extrahieren?
Der zweite Parameter der LEFT-Funktion verwendet ein Array, ROW(1:9) entspricht {1;2;3;4;5;6;7;8;9}. LEFT extrahiert die durch den ersten Parameter angegebenen Daten von links, und die Länge der Extraktion wird durch den zweiten Parameter bestimmt. LEFT extrahiert gemäß dem Array {1;2;3;4;5;6;7;8;9} und erhält 9 Ergebnisse:

, das heißt, es werden Ziffer 1 von links und Ziffer 2 extrahiert. .bis hin zu 9 Bit. Da es sich bei den von LEFT extrahierten Ergebnissen ausschließlich um Texttypen handelt, kann das Hinzufügen eines negativen Vorzeichens vor LEFT die Textnummern in numerische Werte umwandeln, und der Text wird zu einem Fehlerwert:

Der Fehlerwert wird von LOOKUP ignoriert, und Jetzt wird 1 in {-1; -10} gefunden. Gemäß dem Prinzip der binären Suche können wir nach der Halbierung nur nach unten suchen, bis die letzte Ziffer kleiner als 1 ist. Daher können wir einfach verstehen, dass das Wesentliche von LOOKUP darin besteht, die letzten Daten zu finden, wenn der Suchwert größer ist als alle Daten im Suchbereich (unabhängig davon, ob er in aufsteigender Reihenfolge vorliegt).
Tatsächlich ist es auch möglich, 1 in der Formel in 0 zu ändern, denn 0 ist auch größer als alle negativen Zahlen:

Die aktuell letzte Zahl ist -10, also fügen wir davor ein negatives Vorzeichen ein LOOKUP und es wird 10, was die Zahl ist, die wir extrahieren müssen.
Für Anfänger ist die Verwendung von LOOKUP in den beiden oben genannten Fällen zu fortgeschritten. Es wird geschätzt, dass sie nur über geringe Kenntnisse verfügen. Tatsächlich gibt es einen Prozess des Lernens von Funktionen Vom Verstehen bis zum Beherrschen ist hier viel Übung und Nachdenken erforderlich. Solange jeder eine positive und optimistische Einstellung behält und den Spaß an Lernfunktionen erleben kann, ist der Erfolg nicht mehr weit.
Verwandte Lernempfehlungen: Excel-Tutorial
Das obige ist der detaillierte Inhalt vonDas Dichotomieprinzip der LOOKUP-Funktion beim Lernen von Excel-Funktionen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!