CSS3 + JS realisiert 3D-Planetenbewegungen

Dieses Mal werde ich Ihnen CSS3+js zur Verfügung stellen, um 3D-Planetenoperationen zu realisieren.

HTML-Teil

Hier verwenden wir die ersten drei Kategorien von p, um jeden Planeten zu zeichnen: x, y, z x, y- und z-Achsen, und diese Planeten können verschachtelt sein, das heißt, genau wie im obigen Code sind die inneren Planeten Satelliten der äußeren Planeten.

<p class="path-Saturn">
        <p id="Saturn" title="土星">
            <p class="x"></p>  
            <p class="y"></p>
            <p class="z"></p>
            <p class="space space-x"></p>
            <p class="space space-x1"></p>
            <p class="space space-x2"></p>

            <p class="space space-y"></p>
            <p class="space space-y1"></p>
            <p class="space space-y2"></p>

            <p class="space space-z"></p>
            <p class="space space-z1"></p>
            <p class="space space-z2"></p>
    
            <!-- 卫星 -->
            <p class="path-satellite">
                <p id="satellite" title="卫星">
                    <p class="x"></p>
                    <p class="y"></p>
                    <p class="z"></p>
                    <p class="space space-x"></p>
                    <p class="space space-x1"></p>
                    <p class="space space-x2"></p>

                    <p class="space space-y"></p>
                    <p class="space space-y1"></p>
                    <p class="space space-y2"></p>

                    <p class="space space-z"></p>
                    <p class="space space-z1"></p>
                    <p class="space space-z2"></p>
                </p>
            </p>
        </p>
    </p>

CSS-Teil

Verwendet hauptsächlich neun Flächen, um durch verschiedene Drehungen und Verschiebungen eine Kugel zusammenzusetzen. Und da hier kein Kompatibilitätscode geschrieben ist, sollten Freunde, die daran interessiert sind, den Quellcode herunterzuladen, versuchen, ihn mit dem Chrome-Browser zu öffnen. Es gibt mehrere CSS3-Attribute, die hier erwähnt werden müssen:

.path-Saturn, .path-earth, .path-Venus, .path-Neptune, .path-Jupiter, .path-Mercury, .path-satellite, .path-moon{
    position: absolute;
    width: 95%;
    height: 95%;
    top: 2.5%;
    left: 2.5%;
    border: 1px solid #ddd;
    border-radius: 50%;
    transform: rotateX(60deg);
    transform-style: preserve-3d;
}
#sun, #earth, #Saturn, #Venus, #Neptune, #Jupiter, #Mercury, #satellite, #moon{
    width: 160px;
    height: 160px;
    position: absolute;
    transform-style: preserve-3d;
    top: 50%;
    left: 50%;
    margin: -80px 0 0 -80px;
    animation: rotateForward 10s linear infinite;
    cursor: pointer;
    transform: translateZ(-80px);
}
/*x, y, z轴*/
.x, .y, .z{  
    position: absolute;
    height: 100%;
    border: 1px solid #999;
    left: 50%;
    margin-left: -1px;
}
.y{
    transform: rotateZ(90deg);
}
.z{
    transform: rotateX(90deg);
}
@keyframes  rotateForward {
    0%{
        transform: rotate3d(1, 1, 1, 0deg);
    }
    100%{
        transform: rotate3d(1, 1, 1, -360deg);
    }
}
/*Saturn*/
#Saturn{
    width: 80px;
    height: 80px;
    left: 0%;
    margin: -40px 0 0 -40px;
    animation: rotateForward 4s linear infinite;
    transform: translateZ(-40px);
}
#Saturn .space{
    width: 80px;
    height: 80px;
    box-shadow: 0 0 60px rgba(90, 80, 53, 1);
    background-color: rgba(90, 80, 53, .3);
}
#Saturn .space-x1, #Saturn .space-x2, #Saturn .space-y1, #Saturn .space-y2, #Saturn .space-z1, #Saturn .space-z2{
    width: 87.5%;
    height: 87.5%;
    top: 6.25%;
    left: 6.25%;
    transform: rotate3d(0, 0, 0, 0deg) translateZ(20px);
}
#Saturn .space-x1{
    transform: rotate3d(0, 0, 0, 0deg) translateZ(-20px);
}
#Saturn .space-y{
    transform: rotate3d(0, 1, 0, 90deg) translateZ(0px);
}
#Saturn .space-y1{
    transform: rotate3d(0, 1, 0, 90deg) translateZ(-20px);
}
#Saturn .space-y2{
    transform: rotate3d(0, 1, 0, 90deg) translateZ(20px);
}
#Saturn .space-z{
    transform: rotate3d(1, 0, 0, 90deg) translateZ(0px);
}
#Saturn .space-z1{
    transform: rotate3d(1, 0, 0, 90deg) translateZ(-20px);
}
#Saturn .space-z2{
    transform: rotate3d(1, 0, 0, 90deg) translateZ(20px);
}

1. Transform-Style: Preserve-3d wird verwendet, um die untergeordneten Elemente des Containers mit diesem Attributsatz in einem 3D-Effekt anzuzeigen.

2. Transformationsursprung: Legen Sie die Basispunktposition der Drehung und Verschiebung des gedrehten Elements fest.

3. Perspektive: Legen Sie die Ansicht fest, in der das Element angezeigt wird.

JS-Teil

Bei der Implementierung von Planetenbewegungen gibt es einige Stellen, die nicht sehr gut gehandhabt werden, weil ich ihnen auf jeden Fall folge Lassen Sie in Intervallen die linke Position des Planeten ändern und ermitteln Sie dann den Wert von oben gemäß der Ellipsenformel. Da die Ellipse ungleichmäßig ist, erscheint die Bewegung des Planeten schnell und langsam, da sich ihr Spitzenwert ungleichmäßig ändert.

(function(planetObj, TimeArr, judgeDirec) {
    //检测参数是否规范
    var timeRegexp = /^[1-9][0-9]*$/,
        direcRegexp = /^[01]$/;
    function checkArgs (arg, ele, regexp) {
        if(arg){
            $(arg).each(function (i, item) {
                if(arg.length != planetObj.length || !regexp.test(item)){
                    throw Error('an error occured');
                    return;
                }else{
                    return arg;
                }
            })
        }else{
            arg = [];
            for(var i = 0; i < planetObj.length; i++){
                arg.push(ele);
            }
        }
        return arg;
    }
    TimeArr = checkArgs(TimeArr, 50, timeRegexp);
    judgeDirec = checkArgs(judgeDirec, 1, direcRegexp);

    var PathArr = [];
    $(planetObj).each(function (i, item) {
        var n = 0;  //定义一个标识，来判断当前是怎么运动的
        PathArr.push({
            a : $(item).parent().width() / 2,
            b : $(item).parent().height() / 2
        });

        //变化x坐标，然后根据椭圆轨迹，获得y坐标，以达到运动的效果
        function getEllopsePath (x, PathObj) {
            x = x - PathObj.a;
            var m;

            n ? (judgeDirec[i] ? m = 1 : m = -1) : (judgeDirec[i] ? m = -1 : m = 1); //判断开根号求得的y值是否为负数，从而确定旋转方向
            // if(judgeDirec[i]){
            //     n ? (m = judgeDirec[i]) : (m = judgeDirec[i]-2);  
            // }else{
            //     n ? (m = judgeDirec[i] - 1) : (m = judgeDirec[i] + 1);
            // }
            return Math.sqrt((1 - x * x / (PathObj.a * PathObj.a)) * PathObj.b * PathObj.b) * m + PathObj.b; 
        }

        function moving () {
            var x = parseInt($(item).css('left'), 10);
            if(x == 2 * PathArr[i].a){  //到达轨迹的右零界点的时候x减小
                n--;
            }else if (x == 0) {   //到达轨迹的左临界点的时候，x增加
                n++;
            }
            n ? x++ : x--;
            $(item).css({
                'top' : getEllopsePath(x, PathArr[i]) + 'px',
                'left' : x + 'px'
            });
        }

        setInterval(moving, TimeArr[i]);
    });
})(['#Saturn', '#earth', '#Venus', '#Neptune', '#Mercury', '#Jupiter', '#satellite', '#moon'], [40, 180, 240, 20, 120, 200, 30, 10]/*option默认为50毫秒*/, [1, 0, 0, 0, 1, 0, 1, 1]/*option 判断运动方向，0为顺时针，1为逆时针，默认为逆时针*/);

Dann gibt es noch eine weitere Sache, die hier beachtet werden muss, nämlich, dass die von der Math.sqrt()-Methode extrahierten Werte alle positive Zahlen sind, und wenn wir wollen, dass der Planet umkreist, dann tun wir das Sie müssen das linke und rechte Ende der Flugbahn dynamisch anpassen. Ändern Sie die positiven und negativen Zahlen des von der Math.sqrt()-Methode generierten Werts.

Eine Darstellung ist unten beigefügt

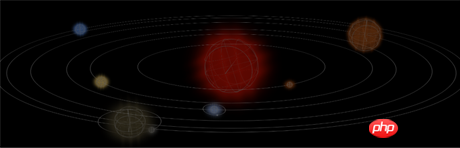Ich glaube, dass Sie die Methode beherrschen, nachdem Sie den Fall gelesen haben Dieser Artikel: Weitere spannende Inhalte finden Sie in anderen verwandten Artikeln auf der chinesischen PHP-Website!

Empfohlene Lektüre:

Detaillierte Erläuterung des dynamischen Ladens von CSS

So verwenden Sie das Webkit-tap-highlight-color-Attribut von CSS3

Das obige ist der detaillierte Inhalt vonCSS3 + JS realisiert 3D-Planetenbewegungen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!