距離測量是有監督和無監督學習演算法的基礎,包括k近鄰、支援向量機和k均值聚類等。
距離測量的選擇會影響我們的機器學習結果,因此考慮哪種測量最適合這個問題是很重要的。因此,我們在決定使用哪種測量方法時應該謹慎。但在做出決定之前,我們需要了解距離測量是如何運作的,以及我們可以從哪些測量中進行選擇。
本文將簡要介紹常用的距離測量方法、它們的工作原理、如何用Python計算它們以及何時使用它們。這樣可以加深知識和理解,提高機器學習演算法和結果。
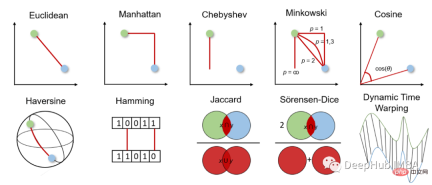
在更深入研究不同的距離測量之前,我們先要有一個關於它們如何運作以及如何選擇合適的測量的大致概念。
距離度量用於計算給定問題空間中兩個物件之間的差異,即資料集中的特徵。然後可以使用該距離來確定特徵之間的相似性, 距離越小特徵越相似。
對於距離的測量,我們可以在幾何距離測量和統計距離測量之間進行選擇,並且應該選擇哪種距離測量取決於資料的類型。特徵可能有不同的資料類型(例如,真實值、布林值、分類值),資料可能是多維的或由地理空間資料組成。
幾何距離測量
1、歐氏距離 Euclidean distance
#歐氏距離度量兩個實值向量之間的最短距離。由於其直觀,使用簡單和對許多用例有良好結果,因此它是最常用的距離度量和許多應用程式的預設距離度量。
歐氏距離也可稱為l2範數,其計算方法為:

Python程式碼如下
from scipy.spatial import distance distance.euclidean(vector_1, vector_2)
歐氏距離有兩個主要缺點。首先,距離測量不適用於比2D或3D空間更高維度的資料。第二,如果我們不將特徵標準化和/或標準化,距離可能會因為單位的不同而傾斜。
2、曼哈頓距離Manhattan distance
曼哈頓距離也被稱為出租車或城市街區距離,因為兩個實值向量之間的距離是根據一個人只能以直角移動計算的。這種距離測量通常用於離散和二元屬性,這樣可以獲得真實的路徑。
曼哈頓距離以l1範數為基礎,計算公式為:
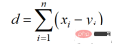
Python程式碼如下
from scipy.spatial import distance distance.cityblock(vector_1, vector_2)
曼哈頓的距離有兩個主要的缺點。它不如高維空間中的歐氏距離直觀,它也沒有顯示可能的最短路徑。雖然這可能沒有問題,但我們應該意識到這並不是最短的距離。
3、切比雪夫距離 Chebyshev distance
切比雪夫距離也稱為棋盤距離,因為它是兩個實值向量之間任意維度上的最大距離。它通常用於倉庫物流中,其中最長的路徑決定了從一個點到另一個點所需的時間。

切比雪夫距離由l -無窮範數計算:

Python程式碼如下
from scipy.spatial import distance distance.chebyshev(vector_1, vector_2)
切比雪夫距離只有非常特定的用例,因此很少使用。
4、閔可夫斯基距離 Minkowski distance
閔可夫斯基距離是上述距離測量的廣義形式。它可以用於相同的用例,同時提供高靈活性。我們可以選擇 p 值來找到最適合的距離測量。

閔可夫斯基距離的計算方法為:
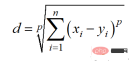
Python程式碼如下
from scipy.spatial import distance distance.minkowski(vector_1, vector_2, p)
由於閔可夫斯基距離表示不同的距離度量,它就有與它們相同的主要缺點,例如在高維空間的問題和對特徵單位的依賴。此外,p值的靈活性也可能是一個缺點,因為它可能會降低計算效率,因為找到正確的p值需要進行多次計算。
5、餘弦相似度和距離 Cosine similarity
餘弦相似度是方向的度量,他的大小由兩個向量之間的餘弦決定,並且忽略了向量的大小。餘弦相似度通常用於與資料大小無關的高維,例如,推薦系統或文字分析。
余弦相似度可以介于-1(相反方向)和1(相同方向)之间,计算方法为:
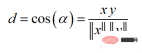
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度,位于0(相似值)和1(不同值)之间。
Python代码如下
from scipy.spatial import distance distance.cosine(vector_1, vector_2)
余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此,没有充分考虑到值的差异。
6、半正矢距离 Haversine distance
半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航,其中经度和纬度和曲率对计算都有影响。
半正矢距离的公式如下:

其中r为球面半径,φ和λ为经度和纬度。
Python代码如下
from sklearn.metrics.pairwise import haversine_distances haversine_distances([vector_1, vector_2])
半正矢距离的主要缺点是假设是一个球体,而这种情况很少出现。
7、汉明距离
汉明距离衡量两个二进制向量或字符串之间的差异。
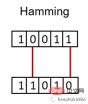
对向量按元素进行比较,并对差异的数量进行平均。如果两个向量相同,得到的距离是0之间,如果两个向量完全不同,得到的距离是1。
Python代码如下
from scipy.spatial import distance distance.hamming(vector_1, vector_2)
汉明距离有两个主要缺点。距离测量只能比较相同长度的向量,它不能给出差异的大小。所以当差异的大小很重要时,不建议使用汉明距离。
统计距离测量
统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。
8、杰卡德指数和距离 Jaccard Index
Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较,或者根据单词的重叠来比较文档中的文本模式。

Jaccard距离的计算方法为:
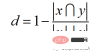
Python代码如下
from scipy.spatial import distance distance.jaccard(vector_1, vector_2)
Jaccard指数和距离的主要缺点是,它受到数据规模的强烈影响,即每个项目的权重与数据集的规模成反比。
9、Sorensen-Dice指数
Sörensen-Dice指数类似于Jaccard指数,它可以衡量的是样本集的相似性和多样性。该指数更直观,因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。
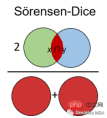
计算公式如下:
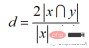
Python代码如下
from scipy.spatial import distance distance.dice(vector_1, vector_2)
它的主要缺点也是受数据集大小的影响很大。
10、动态时间规整 Dynamic Time Warping
动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例,如语音识别或异常检测。
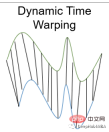
为什么我们需要一个为时间序列进行距离测量的度量呢?如果时间序列长度不同或失真,则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移,那么尽管时间序列非常相似,但欧几里得距离会表现出很大的差异。
动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时,这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离,该路径必须满足以下条件:
- 边界条件:弯曲路径在两个时间序列的起始点和结束点开始和结束
- 单调性条件:保持点的时间顺序,避免时间倒流
- 连续条件:路径转换限制在相邻的时间点上,避免时间跳跃
- 整经窗口条件(可选):允许的点落入给定宽度的整经窗口
- 坡度条件(可选):限制弯曲路径坡度,避免极端运动
我们可以使用 Python 中的 fastdtw 包:
from scipy.spatial.distance import euclidean from fastdtw import fastdtw distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)
动态时间规整的一个主要缺点是与其他距离测量方法相比,它的计算工作量相对较高。
总结
在这篇文章中,简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的,如何在Python中实现它们,以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量,请留言告诉我。
以上是十個機器學習中常用的距離測量方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!
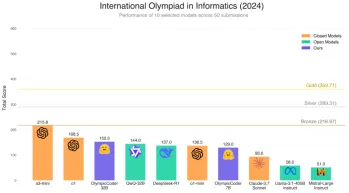 擁抱面部是否7B型號奧林匹克賽車擊敗克勞德3.7?Apr 23, 2025 am 11:49 AM
擁抱面部是否7B型號奧林匹克賽車擊敗克勞德3.7?Apr 23, 2025 am 11:49 AM擁抱Face的OlympicCoder-7B:強大的開源代碼推理模型 開發以代碼為中心的語言模型的競賽正在加劇,擁抱面孔與強大的競爭者一起參加了比賽:OlympicCoder-7B,一種產品
 4個新的雙子座功能您可以錯過Apr 23, 2025 am 11:48 AM
4個新的雙子座功能您可以錯過Apr 23, 2025 am 11:48 AM你們當中有多少人希望AI可以做更多的事情,而不僅僅是回答問題?我知道我有,最近,我對它的變化感到驚訝。 AI聊天機器人不僅要聊天,還關心創建,研究
 Camunda為經紀人AI編排編寫了新的分數Apr 23, 2025 am 11:46 AM
Camunda為經紀人AI編排編寫了新的分數Apr 23, 2025 am 11:46 AM隨著智能AI開始融入企業軟件平台和應用程序的各個層面(我們必須強調的是,既有強大的核心工具,也有一些不太可靠的模擬工具),我們需要一套新的基礎設施能力來管理這些智能體。 總部位於德國柏林的流程編排公司Camunda認為,它可以幫助智能AI發揮其應有的作用,並與新的數字工作場所中的準確業務目標和規則保持一致。該公司目前提供智能編排功能,旨在幫助組織建模、部署和管理AI智能體。 從實際的軟件工程角度來看,這意味著什麼? 確定性與非確定性流程的融合 該公司表示,關鍵在於允許用戶(通常是數據科學家、軟件
 策劃的企業AI體驗是否有價值?Apr 23, 2025 am 11:45 AM
策劃的企業AI體驗是否有價值?Apr 23, 2025 am 11:45 AM參加Google Cloud Next '25,我渴望看到Google如何區分其AI產品。 有關代理空間(此處討論)和客戶體驗套件(此處討論)的最新公告很有希望,強調了商業價值
 如何為抹布找到最佳的多語言嵌入模型?Apr 23, 2025 am 11:44 AM
如何為抹布找到最佳的多語言嵌入模型?Apr 23, 2025 am 11:44 AM為您的檢索增強發電(RAG)系統選擇最佳的多語言嵌入模型 在當今的相互聯繫的世界中,建立有效的多語言AI系統至關重要。 強大的多語言嵌入模型對於RE至關重要
 麝香:奧斯汀的機器人需要每10,000英里進行干預Apr 23, 2025 am 11:42 AM
麝香:奧斯汀的機器人需要每10,000英里進行干預Apr 23, 2025 am 11:42 AM特斯拉的Austin Robotaxi發射:仔細觀察Musk的主張 埃隆·馬斯克(Elon Musk)最近宣布,特斯拉即將在德克薩斯州奧斯汀推出的Robotaxi發射,最初出於安全原因部署了一支小型10-20輛汽車,並有快速擴張的計劃。 h
 AI震驚的樞軸:從工作工具到數字治療師和生活教練Apr 23, 2025 am 11:41 AM
AI震驚的樞軸:從工作工具到數字治療師和生活教練Apr 23, 2025 am 11:41 AM人工智能的應用方式可能出乎意料。最初,我們很多人可能認為它主要用於代勞創意和技術任務,例如編寫代碼和創作內容。 然而,哈佛商業評論最近報導的一項調查表明情況並非如此。大多數用戶尋求人工智能的並非是代勞工作,而是支持、組織,甚至是友誼! 報告稱,人工智能應用案例的首位是治療和陪伴。這表明其全天候可用性以及提供匿名、誠實建議和反饋的能力非常有價值。 另一方面,營銷任務(例如撰寫博客、創建社交媒體帖子或廣告文案)在流行用途列表中的排名要低得多。 這是為什麼呢?讓我們看看研究結果及其對我們人類如何繼續將


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

記事本++7.3.1
好用且免費的程式碼編輯器

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境







