廣度優先遍歷類似二元樹的什麼遍歷?
- 青灯夜游原創
- 2020-07-25 13:46:1910802瀏覽
廣度優先遍歷類似二元樹的層次遍歷。廣度優先搜尋是從根結點開始沿著樹的寬度搜尋遍歷,也就是按層次的去遍歷;從上往下對每一層依次訪問,在每一層中,從左往右(也可以從右往左)訪問結點,訪問完一層就進入下一層,直到沒有結點可以訪問為止。

廣度優先搜尋(Breadth First Search)(其實是二元樹的層次遍歷),又叫寬度優先搜尋或橫向優先搜索,是從根結點開始沿著樹的寬度搜尋遍歷。
從上往下對每一層依次訪問,在每一層中,從左往右(也可以從右往左)訪問結點,訪問完一層就進入下一層,直到沒有結點可以訪問為止。
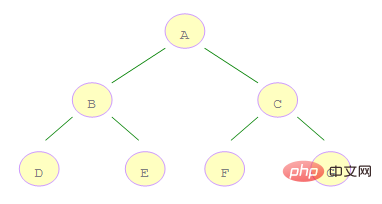
上面二元樹的遍歷順序為:ABCDEFG. 可以利用佇列實作廣度優先搜尋。
廣度優先搜尋演算法:
保留全部結點,佔用空間大;無回溯操作(即無入堆疊、出棧操作),運行速度快。
廣度優先搜尋演算法,一般需儲存產生的所有結點,佔用的儲存空間要比深度優先搜尋大得多,因此,程式設計中,必須考慮溢出和節省記憶體空間的問題。但廣度優先搜尋法一般無回溯操作,即入棧和出棧的操作,所以運行速度比深度優先搜尋快些。
範例:
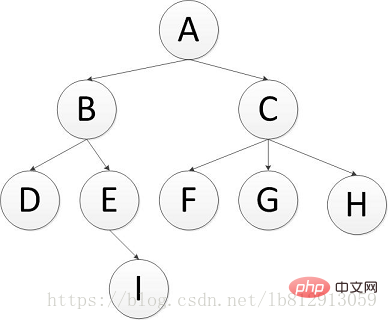
#其過程檢定來說是對每一層節點依序訪問,訪問完一層進入下一層,而且每個節點只能訪問一次。對於上面的例子來說,廣度優先遍歷的 結果是:A,B,C,D,E,F,G,H,I(假設每層節點從左到右訪問)。
廣度優先遍歷各個節點,需要使用到隊列(Queue)這種資料結構,queue的特點是先進先出,其實也可以使用雙端隊列,區別就是雙端隊列首位都可以插入和彈出節點。整個遍歷過程如下:
首先將A節點插入佇列中,queue(A);
將A節點彈出,同時將A的子節點B,C插入佇列中,此時B在佇列首,C在佇列尾部,queue(B,C);
將B節點彈出,同時將B的子節點D,E插入佇列中,此時C在佇列首,E在佇列尾部,queue(C,D,E);
將C節點彈出,同時將C的子節點F,G,H插入佇列中,此時D在佇列首,H在佇列尾部,queue(D,E,F,G,H);
將D節點彈出,D沒有子節點,此時E在佇列首,H在佇列尾部,queue(E,F, G,H);
...依序往下,最後遍歷完成
Java程式碼大概如下:
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public class Solution {
public ArrayList<Integer> wide(TreeNode root) {
ArrayList<Integer> lists=new ArrayList<Integer>();
if(root==null)
return lists;
Queue<TreeNode> queue=new LinkedList<TreeNode>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode node = queue.poll();
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
lists.add(node.val);
}
return lists;
}
}更多相關知識,請造訪: PHP中文網!
以上是廣度優先遍歷類似二元樹的什麼遍歷?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

