深度優先遍歷與廣度優先遍歷

深度優先遍歷

假設給定圖G的初態是所有頂點均未曾造訪過。在G中任選一頂點v為初始出發點(源點)，則深度優先遍歷可定義如下：首先訪問出發點v，並將其標記為已訪問過；然後依次從v出發搜尋v的每個鄰接點w。 (推薦學習：web前端視訊教學）

若w未曾造訪過，則以w為新的出發點繼續進行深度優先遍歷，直至圖中所有和來源點v有路徑相通的頂點(亦稱為從源點可達的頂點)均已被存取為止。

若此時圖中仍有未訪問的頂點，則另選一個尚未訪問的頂點作為新的來源點重複上述過程，直至圖中所有頂點均已被訪問為止。

圖的深度優先遍歷類似於樹的前序遍歷。所採用的搜尋方法的特點是盡可能先對縱深方向進行搜尋。這種搜尋方法稱為深度優先搜尋(Depth-First Search)。相應地，用此方法遍歷圖就很自然地稱之為圖的深度優先遍歷。

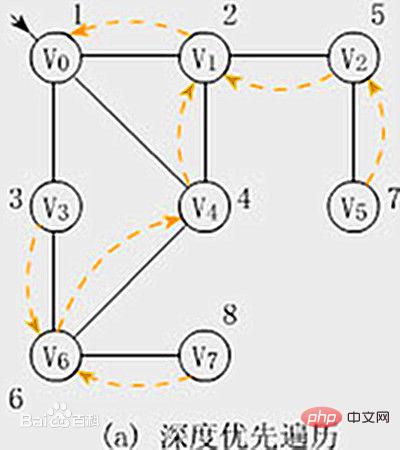
說白了深度優先遍歷就是一種不撞南牆不會頭的演算法，他會把一條路走完之後再回溯到有分叉的節點繼續遍歷。

如圖：

#廣度優先遍歷

從圖中某個頂點V0出發，並訪問此頂點；

從V0出發，訪問V0的各個未曾訪問的鄰接點W1，W2，…,Wk;然後,依次從W1,W2,…,Wk出發訪問各自未被訪問的鄰接點；

重複步驟2，直到全部頂點都被訪問為止。

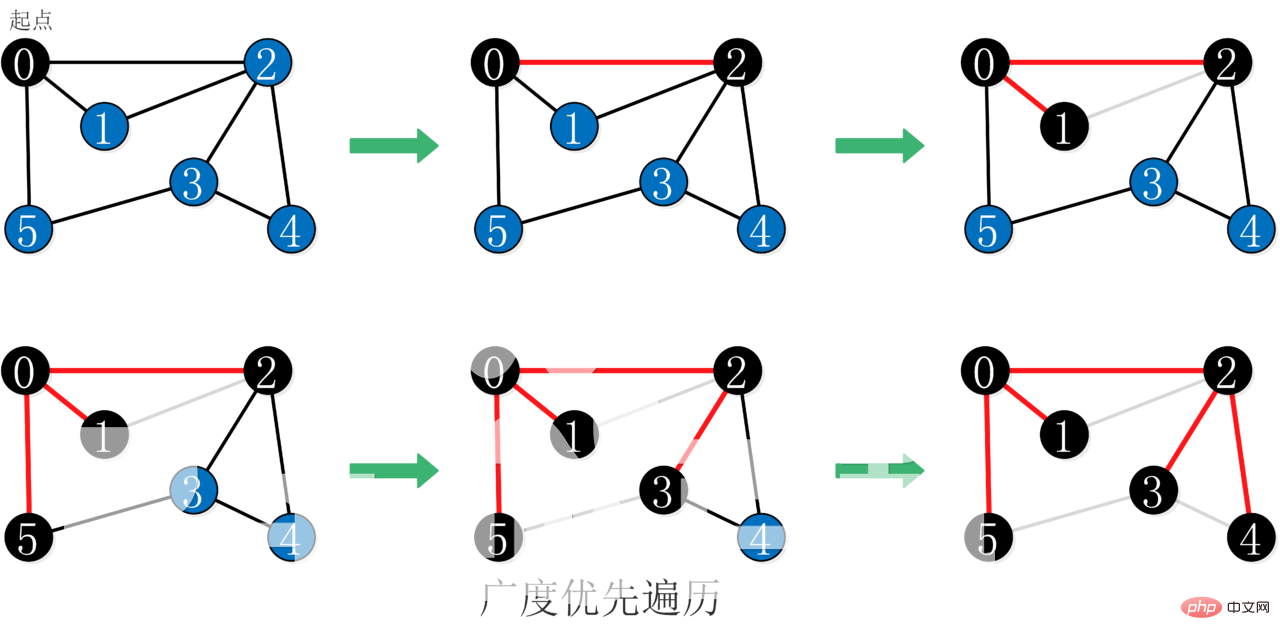
這是一種層層遞進的演算法，與樹的層序遍歷類似。

在廣度優先搜尋時，會從起點開始「一層一層」擴展的方法來遍歷，擴展時每發現一個點就將這個點加入到隊列，直到整張圖都被遍歷過位置。

以上是深度優先遍歷與廣度優先遍歷的詳細內容。更多資訊請關注PHP中文網其他相關文章！