二元樹的基本性質

在電腦科學中，二元樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱為「左子樹」（left subtree）和「右子樹」（right subtree）。二元樹常被用來實現二元查找樹和二元堆。

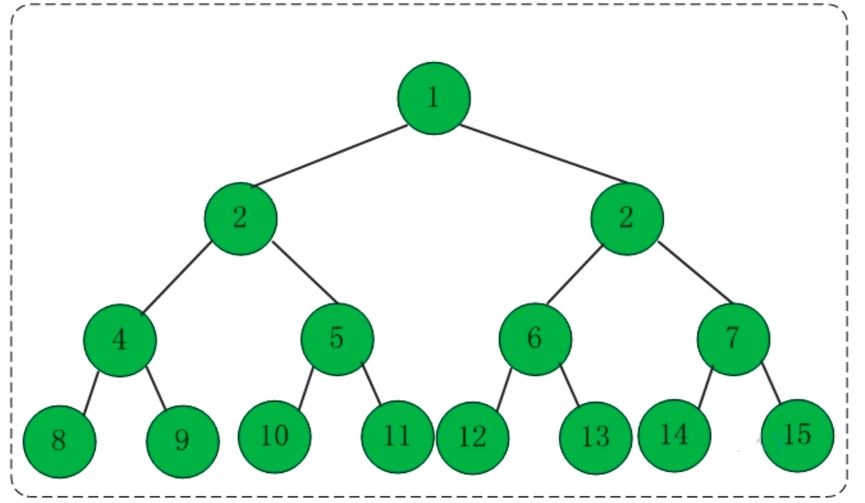
一棵深度為k，且有2^k-1個節點的二元樹，稱為滿二元樹。這種樹的特徵是每一層上的節點數都是最大節點數。而在一棵二元樹中，除最後一層外，若其餘層都是滿的，並且最後一層或者是滿的，或者是在右邊缺少連續若干節點，則此二叉樹為完全二叉樹。具有n個節點的完全二元樹的深度為floor(log2n) 1。深度為k的完全二元樹，至少有2k-1個葉子節點，至多有2k-1個節點。

二元樹性質

(1) 在非空二元樹中，第i層的結點總數不超過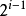, i>=1;

(2) 深度為h的二元樹最多有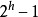個結點(h>=1)，最少有h個結點；

(3) 對於任一棵二元樹，如果其葉結點數為N0，而度數為2的結點總數為N2，則N0=N2 1；

(4) 具有n個結點的完全二元樹的深度為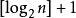（註：[ ]表示向下取整）

推薦課程：PHP教學。

(5)有N個結點的完全二元樹各結點如果用順序方式存儲，則結點之間有如下關係：

若I為結點編號則如果I> ;1，則其父結點的編號為I/2；

若2*I<=N，則其左孩子（即左子樹的根結點）的編號為2*I；若2*I>N，則無左孩子；

若2*I 1<=N，則其右孩子的結點編號為2*I 1；若2*I 1>N，則無右孩子。

(6)給定N個節點，能構成h(N)種不同的二元樹。

h(N)為卡特蘭數的第N項。 h(n)=C(2*n，n)/(n 1)。

(7)設有i個枝點，I為所有枝點的道路長度總和，J為葉的道路長度總和J=I 2i [2] 

基本概念

二元樹是遞歸定義的，其結點有左右子樹之分，邏輯上二元樹有五種基本形態：

(1)空二叉樹－如圖(a)；

(2)只有一個根結點的二元樹－如圖(b)；

(3)只有左子樹－如圖(c)；

(4)只有右子樹－如圖(d)；

(5)完全二元樹－如圖(e)。

注意：儘管二元樹與樹有許多相似之處，但二元樹不是樹的特殊情況。 [1] 

類型

(1)完全二元樹－若設二元樹的高度為h，除第h 層外，其它各層(1～h -1) 的結點數都達到最大個數，第h層有葉子結點，葉子結點都是從左到右依序排布，這就是完全二元樹。

(2)滿二元樹－除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二元樹。

(3)平衡二元樹－平衡二元樹又被稱為AVL樹（區別於AVL演算法），它是一棵二元排序樹，且具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二元樹。

辨別

二元樹不是樹的一種特殊情形，儘管其與樹有許多相似之處，但樹和二元樹有兩個主要差別：

1. 樹中結點的最大度數沒有限制，而二元樹結點的最大度數為2；

2. 樹的結點無左、右之分，而二元樹的結點有左、右之分。

以上是二元樹的基本性質的詳細內容。更多資訊請關注PHP中文網其他相關文章！