JavaScript中二元樹（二元堆）的介紹（程式碼範例）

這篇文章帶給大家的內容是關於JavaScript中二元樹（二元堆）的介紹（程式碼範例），有一定的參考價值，有需要的朋友可以參考一下，希望對你有幫助。

二元樹

二元樹(Binary Tree)是一種樹狀結構，它的特徵是每個節點最多只有兩個分支節點，一棵二元樹通常由根節點，分支節點，葉節點組成。而每個分支節點也常被稱為一棵子樹。

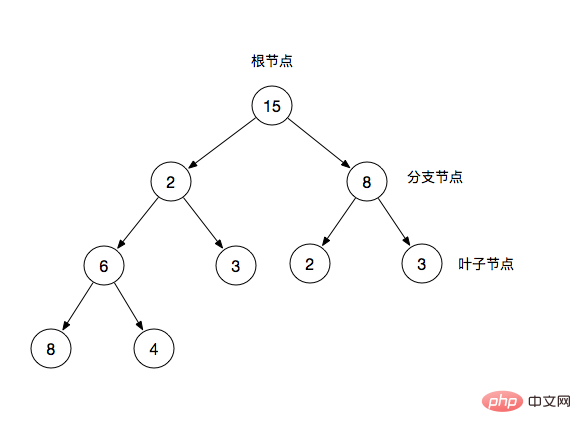
• 根節點：二元樹最頂層的節點

• ## 分支節點：除了根節點以外且擁有葉子節點

• 葉子節點：除了自身，沒有其他子節點

##常用術語

在二元樹中，我們常常也會用父節點和子節點來描述，比如圖中2為6和3的父節點，反之6和3是2子節點

二元樹的三個性質

在二元樹的第i層上，至多有2^i-1個節點

i=1時，只有一個根節點，2^(i-1) = 2^0 = 1

深度為k的二元樹至多有2^k-1個節點

i=2時，2^k-1 = 2^2 - 1 = 3個節點

對任何一棵二元樹T，若總結點數為n0，度為2(子樹數目為2)的節點數為n2,則n0=n2 1

#樹和二元樹的三個主要差異

樹的節點個數至少為1，而二元樹的節點個數可以為0
樹中節點的最大度數(節點數量)沒有限制,而二元樹的節點的最大度數為2
樹的節點沒有左右之分，而二元樹的節點有左右之分
二元樹分類

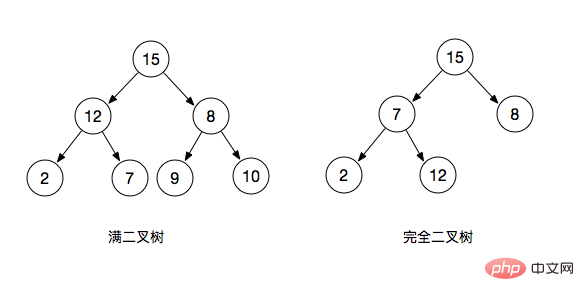
二元樹分為完全二元樹(complete binary tree)和滿二元樹(full binary tree)

#滿二元樹：一棵深度為k且有2^k - 1個節點的二元樹稱為滿二叉樹
完全二元樹：完全二元樹是指最後一層左邊是滿的，右邊可能滿也可能不滿，然後其餘層都是滿的二元樹稱為完全二叉樹(滿二叉樹也是一種完全二叉樹)

二元樹的陣列表示

用一個陣列來表示二元樹的結構，將一組陣列從根節點開始從上到下，從左到右依序填入到一棵完全二元樹中，如下圖所示

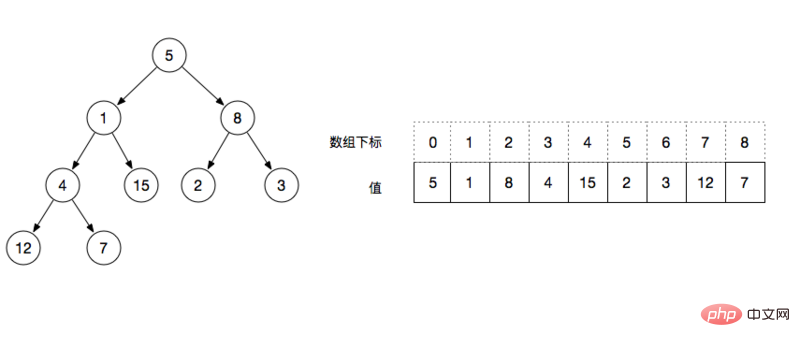#透過上圖我們可以分析得到陣列表示的完全二元樹擁有以下幾個性質：

left = index * 2 1，例如：根節點的下標為0，則左節點的值為下標array[0＊2 1]=1
#right = index * 2 2，例如：根節點的下標為0，則右節點的值為下標array[0＊2 2]=2
序數>= floor(N/2)都是葉子節點，例如：floor(9/2) = 4，則從下標4開始的值都為葉子節點

• ##二元堆

二元堆由一棵完全二元樹來表示其結構，用一個陣列來表示，但一個二元堆需要滿足如下性質：

二元堆的父節點的鍵值總是大於或等於(小於或等於)任何一個子節點的鍵值

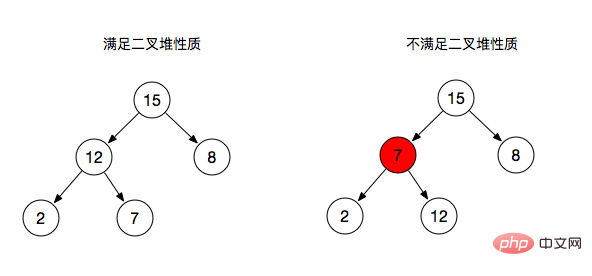
• 當父節點的鍵值大於或等於(小於或等於)它的每一個子節點的鍵值時，稱為
最大堆（最小堆）

• 

  #從上圖可以看出：

#左圖：父節點總是大於或等於其子節點，所以滿足了二元堆的性質，

• 右圖：分支節點7作為2和12的父節點並沒有滿足其性質(大於或等於子節點)。

• 二元堆疊的主要操作

insert：插入節點

• delete：刪除節點

• max-hepify：調整分支節點堆性質

• #rebuildHeap：重新建構整個二元堆

• sort：排序

• 初始化一個二元堆

從上面簡單的介紹，我們可以知道，一個二元堆的初始化非常的簡單，它就是一個陣列

初始化一個陣列結構

• 儲存陣列長度

    class Heap{
        constructor(arr){
            this.data = [...arr];
            this.size = this.data.length;
        }
    }

max-heapify最大堆操作

max-heapify是把每一個不滿足最大堆性質的分支節點進行調整的一個操作。

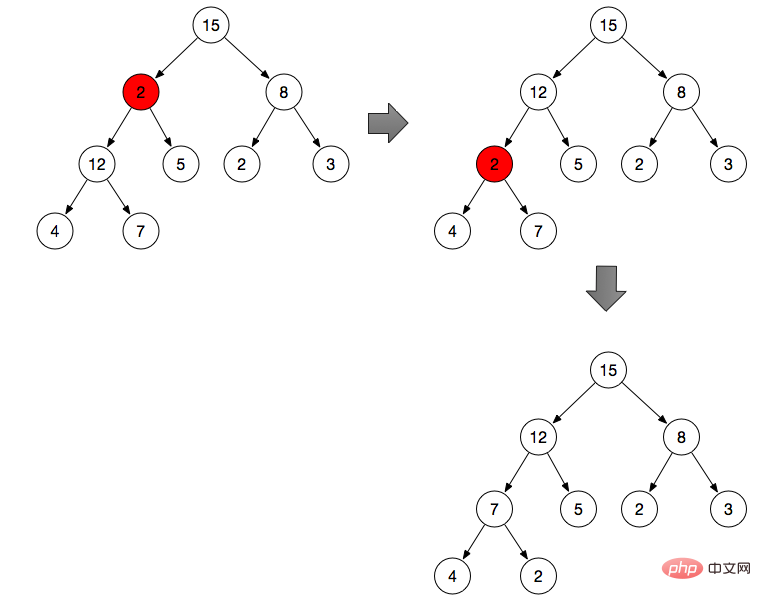
如上圖：

1. #調整分支節點2（分支節點2不滿足最大堆的性質)

• 預設該分支節點為最大值

#將2與左右分支比較，從2，12， 5中找出最大值，然後和2交換位置

• 根據上面所將的二元堆性質，分別得到分支節點2的左節點和右節點

• 比較三個節點，得到最大值的下標max

• #如果該節點本身就是最大值，則停止操作

• 將max節點與父節點交換

重複step2的運算，從2，4，7找出最大值與2做交換

• 遞迴

    maxHeapify(i) {
        let max = i;
        
        if(i >= this.size){
            return;
        }
        // 当前序号的左节点
        const l = i * 2 + 1;
        // 当前需要的右节点
        const r = i * 2 + 2;
        
        // 求当前节点与其左右节点三者中的最大值
        if(l  this.data[max]){
            max = l;
        }
        if(r  this.data[max]){
            max = r;
        }
        
        // 最终max节点是其本身,则已经满足最大堆性质，停止操作
        if(max === i) {
            return;
        }
        
        // 父节点与最大值节点做交换
        const t = this.data[i];
        this.data[i] = this.data[max];
        this.data[max] = t;
        
        // 递归向下继续执行
        return this.maxHeapify(max);
    }

重構堆

我們可以看到，剛初始化的堆由陣列表示，這時候它可能無法滿足一個最大堆或最小堆的性質，而這個時候我們可能需要去將整個堆建成我們想要的。
上面我們做了max-heapify操作，而max-heapify只是將某一個分支節點進行調整，而要將整個堆構建成最大堆，則需要將所有的分支節點都進行一次max-heapify操作，如下圖，我們需要依序對12，3，2，15這4個分支節點進行max-hepify操作

##具體步驟：

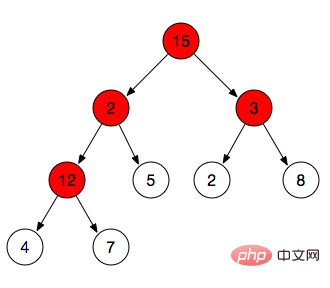
• 找到所有分支節點：上面堆的性質提到過葉子節點的序號>=Math.floor(n/2)，因此小於Math.floor(n/2)序號的都是我們需要調整的節點。

• 例如途中所示數組為[15,2,3,12,5,2,8,4,7] => Math.floor(9/2 )=4 => index小於4的分別是15，2，3，12(需要調整的節點)，而5，2，8，4，7為葉子節點。

• 將找到的節點都進行maxHeapify操作

#

    rebuildHeap(){
        // 叶子节点
        const L = Math.floor(this.size / 2);
        for(let i = L - 1; i>=0; i--){
            this,maxHeapify(i);
        }
    }

最大堆排序

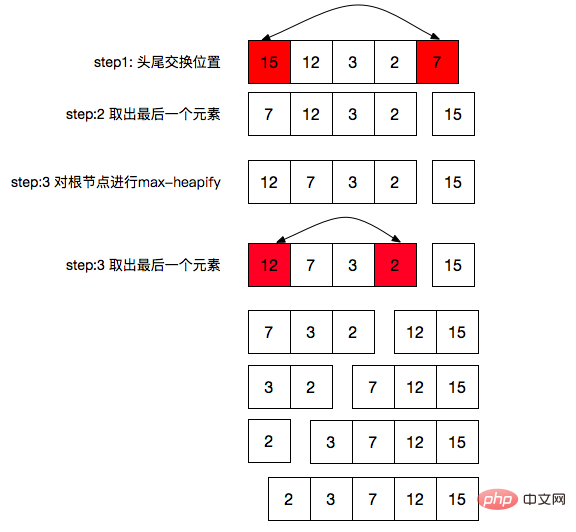
##最大堆的排序，如上圖所示：
#交換首尾位置

將最後個元素從堆中拿出，相當於堆的size-1

• 然後在堆根節點進行一次max-heapify操作

• ##重複以上三個步驟，知道size=0 (這個邊界條件我們在max-heapify函數裡已經做了)

#

    sort() {
        for(let i = this.size - 1; i > 0; i--){
            swap(this.data, 0, i);
            this.size--;
            this.maxHeapify(0);
        }
    }

插入和刪除

這個的插入和刪除就相對比較簡單了，就是對一個數組進行插入和刪除的操作

往末尾插入

• 堆長度1

• 判斷插入後是否還是一個最大堆

• 不是則進行重構堆

  insert(key) {
    this.data[this.size] = key;
    this.size++
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

刪除陣列中的某個元素

堆長度-1

#判斷是否是一個堆疊################################################### ######不是則重構堆#########

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

###完整程式碼###

/**
 * 最大堆
 */

function left(i) {
  return i * 2 + 1;
}

function right(i) {
  return i * 2 + 2;
}

function swap(A, i, j) {
  const t = A[i];
  A[i] = A[j];
  A[j] = t;
}

class Heap {
  constructor(arr) {
    this.data = [...arr];
    this.size = this.data.length;
  }

  /**
   * 重构堆
   */
  rebuildHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i--) {
      this.maxHeapify(i);
    }
  }

  isHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i++) {
      const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
      const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;

      const max = Math.max(this.data[i], l, r);

      if (max !== this.data[i]) {
        return false;
      }
      return true;
    }
  }

  sort() {
    for (let i = this.size - 1; i > 0; i--) {
      swap(this.data, 0, i);
      this.size--;
      this.maxHeapify(0);
    }
  }

  insert(key) {
    this.data[this.size++] = key;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  /**
   * 堆的其他地方都满足性质
   * 唯独跟节点，重构堆性质
   * @param {*} i
   */
  maxHeapify(i) {
    let max = i;

    if (i >= this.size) {
      return;
    }

    // 求左右节点中较大的序号
    const l = left(i);
    const r = right(i);
    if (l  this.data[max]) {
      max = l;
    }

    if (r  this.data[max]) {
      max = r;
    }

    // 如果当前节点最大，已经是最大堆
    if (max === i) {
      return;
    }

    swap(this.data, i, max);

    // 递归向下继续执行
    return this.maxHeapify(max);
  }
}

module.exports = Heap;

###總結######堆講到這裡就結束了，堆在二元樹裡相對會比較簡單，常常被用來做排序和優先權佇列等。堆中比較核心的還是max-heapify這個操作，以及堆的三個性質。 ###

以上是JavaScript中二元樹（二元堆）的介紹（程式碼範例）的詳細內容。更多資訊請關注PHP中文網其他相關文章！