11 kaedah asas untuk menentukan kenormalan taburan data

Dalam bidang sains data dan pembelajaran mesin, banyak model mengandaikan bahawa data diedarkan secara normal, atau data menunjukkan prestasi yang lebih baik di bawah taburan normal. Sebagai contoh, regresi linear mengandaikan bahawa sisa adalah taburan normal, dan analisis diskriminasi linear (LDA) diperoleh berdasarkan andaian seperti taburan normal. Oleh itu, memahami cara menguji kenormalan data adalah penting untuk saintis data dan pengamal pembelajaran mesin

Artikel ini bertujuan untuk memperkenalkan 11 kaedah asas untuk menguji kenormalan data untuk membantu pembaca lebih memahami ciri-ciri pengedaran data dan belajar bagaimana menggunakan kaedah yang sesuai untuk analisis. Ini boleh mengendalikan impak pengedaran data dengan lebih baik pada prestasi model, dan menjadi lebih selesa dalam proses pembelajaran mesin dan pemodelan data

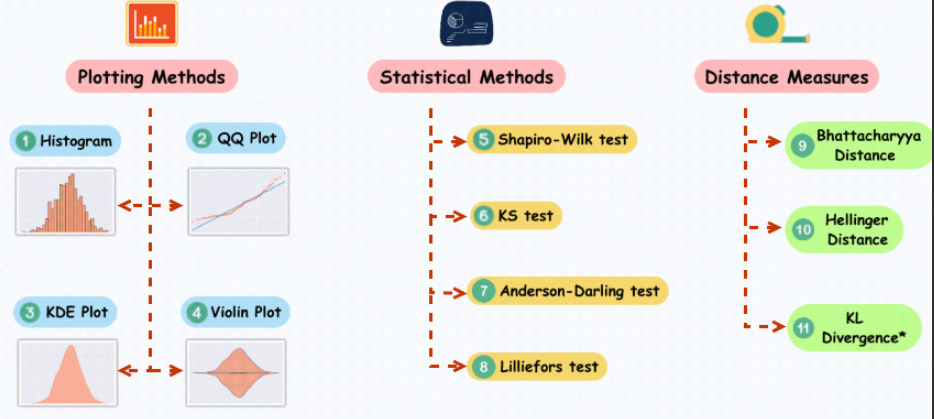
Kaedah Ploting

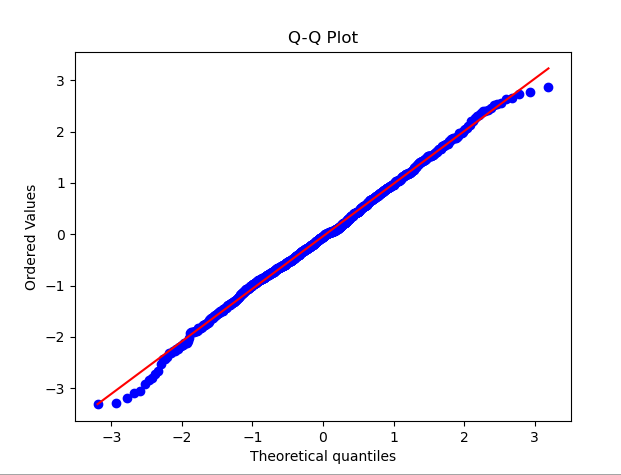
1) ialah kaedah yang digunakan secara meluas untuk menyemak sama ada sesuatu data taburan menepati taburan normal. Dalam plot QQ, kuantiti data dibandingkan dengan kuantiti taburan normal piawai Jika taburan data hampir dengan taburan normal, titik-titik pada plot QQ akan mendekati garis lurus

Untuk menunjukkan. Plot QQ, berikut Kod sampel menjana satu set data rawak yang mengikuti taburan normal. Selepas menjalankan kod, anda boleh melihat plot QQ bersama-sama dengan keluk taburan normal yang sepadan. Dengan memerhati taburan titik pada graf, anda boleh menilai pada mulanya sama ada data adalah hampir kepada taburan normal

import numpy as npimport scipy.stats as statsimport matplotlib.pyplot as plt# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制QQ图stats.probplot(data, dist="norm", plot=plt)plt.title('Q-Q Plot')plt.show()

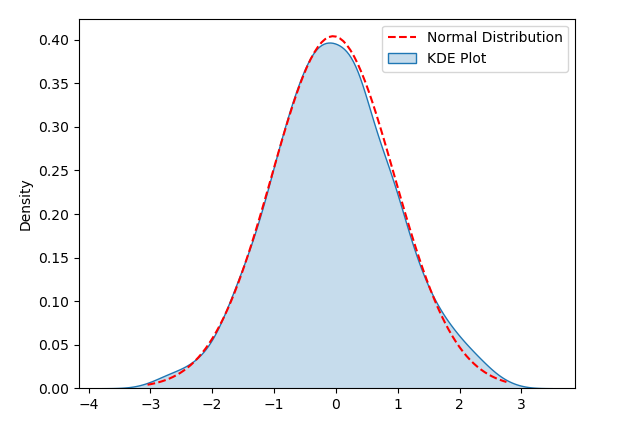
2 Plot KDE

KDE (Anggaran Ketumpatan Kernel) ialah kaedah untuk menggambarkan taburan data, yang boleh membantu Kami menguji data untuk kenormalan. Dalam plot KDE, dengan menganggarkan ketumpatan data dan menariknya ke dalam lengkung yang lancar, ia membantu kami memerhati bentuk taburan data

Untuk menunjukkan Plot KDE, kod sampel berikut menjana satu set data rawak yang mematuhi a taburan normal. Selepas menjalankan kod, anda boleh melihat Plot KDE dan lengkung taburan normal yang sepadan, dan menggunakan visualisasi untuk mengesan sama ada taburan data mematuhi kenormalan

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=1000)# 创建KDE Plotsns.kdeplot(data, shade=True, label='KDE Plot')# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

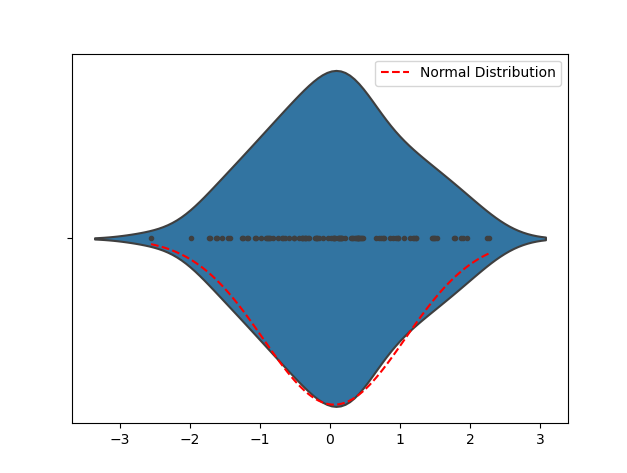
3 Plot Violin

Anda boleh menemui taburan data dengan memerhatikan bentuk Plot Violin untuk menentukan pada mulanya sama ada data itu hampir kepada taburan normal. Jika Plot Violin mempunyai bentuk seperti lengkung loceng, data mungkin lebih kurang taburan normal. Jika Plot Violin anda sangat condong atau mempunyai beberapa puncak, data mungkin tidak diedarkan secara normal.

Kod contoh berikut digunakan untuk menjana data rawak mengikut taburan normal untuk menunjukkan Plot Violin. Selepas menjalankan kod, anda boleh melihat Plot Violin dan lengkung taburan normal yang sepadan. Kesan bentuk taburan data melalui visualisasi untuk menilai pada mulanya sama ada data itu hampir kepada taburan normal

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=100)# 创建 Violin Plotsns.violinplot(data, inner="points")# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

4.Histogram

Menggunakan histogram (Histogram) untuk mengesan kenormalan taburan data juga adalah perkara biasa kaedah. Histogram boleh membantu kita memahami secara intuitif taburan data, dan boleh menentukan awal sama ada data itu hampir kepada taburan normal

import numpy as npimport matplotlib.pyplot as pltimport scipy.stats as stats# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制直方图plt.hist(data, bins=30, density=True, alpha=0.6, color='g')plt.title('Histogram of Data')plt.xlabel('Value')plt.ylabel('Frequency')# 绘制正态分布的概率密度函数xmin, xmax = plt.xlim()x = np.linspace(xmin, xmax, 100)p = stats.norm.pdf(x, np.mean(data), np.std(data))plt.plot(x, p, 'k', linewidth=2)plt.show()

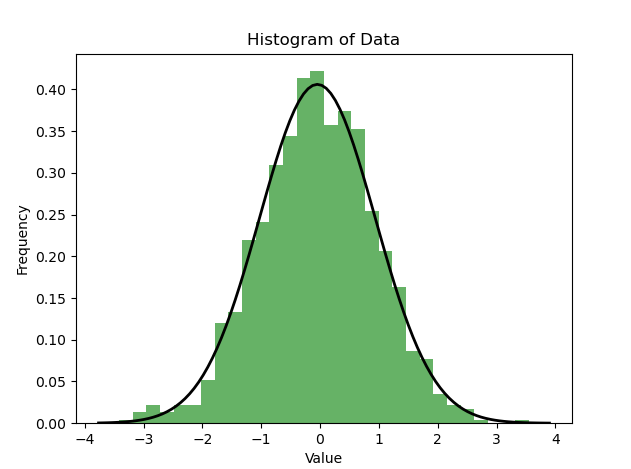Seperti yang ditunjukkan dalam rajah di atas, jika histogram lebih kurang menunjukkan lengkung berbentuk loceng dan adalah konsisten dengan taburan normal yang sepadan Jika bentuk lengkung adalah serupa, maka data berkemungkinan bertaburan normal. Sudah tentu, visualisasi hanyalah pertimbangan awal Jika pengesanan yang lebih tepat diperlukan, kaedah statistik seperti ujian normaliti boleh digunakan untuk analisis.

Kaedah Statistik

5. Ujian Shapiro-Wilk

Ujian Shapiro-Wilk ialah kaedah statistik yang digunakan untuk menguji sama ada data mematuhi taburan normal, juga dikenali sebagai ujian W. Apabila melakukan ujian Shapiro-Wilk, kami biasanya menumpukan pada dua petunjuk utama:

Statistik W: Kira statistik W berdasarkan korelasi antara data yang diperhatikan dan nilai yang dijangkakan di bawah taburan normal, dan julat nilai W Antara 0 dan 1, apabila W menghampiri 1, ini bermakna data yang diperhatikan lebih sesuai dengan taburan normal.

• Nilai P: Nilai P menunjukkan kemungkinan memerhatikan korelasi ini Jika nilai P lebih besar daripada aras keertian (biasanya 0.05), ia menunjukkan bahawa data yang diperhatikan berkemungkinan datang daripada taburan normal.
• Oleh itu, apabila statistik W menghampiri 1 dan nilai P lebih besar daripada 0.05, kita boleh membuat kesimpulan bahawa data yang diperhatikan memenuhi taburan normal.

Dalam kod berikut, satu set data rawak yang mematuhi taburan normal pertama kali dihasilkan, dan kemudian ujian Shapiro-Wilk dilakukan untuk mendapatkan statistik ujian dan nilai P. Berdasarkan perbandingan antara nilai P dan aras keertian, anda boleh menentukan sama ada data sampel datang daripada taburan normal.

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk检验stat, p = stats.shapiro(data)print('Shapiro-Wilk Statistic:', stat)print('P-value:', p)# 根据P值判断正态性alpha = 0.05if p > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

6.KS检验

KS检验（Kolmogorov-Smirnov检验）是一种用于检验数据是否符合特定分布（例如正态分布）的统计方法。它通过计算观测数据与理论分布的累积分布函数（CDF）之间的最大差异来评估它们是否来自同一分布。其基本步骤如下：

• 对两个样本数据进行排序。
• 计算两个样本的经验累积分布函数(ECDF)，即计算每个值在样本中的累积百分比。
• 计算两个累积分布函数之间的差异，通常使用KS统计量衡量。
• 根据样本的大小和显著性水平，使用参考表活计算p值判断两个样本是否来自同一分布。

Python中使用KS检验来检验数据是否符合正态分布时，可以使用Scipy库中的kstest函数。下面是一个简单的示例，演示了如何使用Python进行KS检验来检验数据是否符合正态分布。

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行KS检验statistic, p_value = stats.kstest(data, 'norm')print('KS Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

7.Anderson-Darling检验

Anderson-Darling检验是一种用于检验数据是否来自特定分布（例如正态分布）的统计方法。它特别强调观察值在分布尾部的差异，因此在检测极端值的偏差方面非常有效

下面的代码使用stats.anderson函数执行Anderson-Darling检验，并获取检验统计量、临界值以及显著性水平。然后通过比较统计量和临界值，可以判断样本数据是否符合正态分布

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Anderson-Darling检验result = stats.anderson(data, dist='norm')print('Anderson-Darling Statistic:', result.statistic)print('Critical Values:', result.critical_values)print('Significance Level:', result.significance_level)# 判断正态性if result.statistic <p style="text-align:center;"><img src="https://img.php.cn/upload/article/000/887/227/170255826239547.png" alt="11 kaedah asas untuk menentukan kenormalan taburan data"></p><h4>8.Lilliefors检验</h4><p>Lilliefors检验（也被称为Kolmogorov-Smirnov-Lilliefors检验）是一种用于检验数据是否符合正态分布的统计检验方法。它是Kolmogorov-Smirnov检验的一种变体，专门用于小样本情况。与K-S检验不同，Lilliefors检验不需要假定数据的分布类型，而是基于观测数据来评估是否符合正态分布</p><p>在下面的例子中，我们使用lilliefors函数进行Lilliefors检验，并获得了检验统计量和P值。通过将P值与显著性水平进行比较，我们可以判断样本数据是否符合正态分布</p><pre class="brush:php;toolbar:false">import numpy as npfrom statsmodels.stats.diagnostic import lilliefors# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Lilliefors检验statistic, p_value = lilliefors(data)print('Lilliefors Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

9.距离测量Distance Measures

距离测量（Distance measures）是一种有效的测试数据正态性的方法，它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。

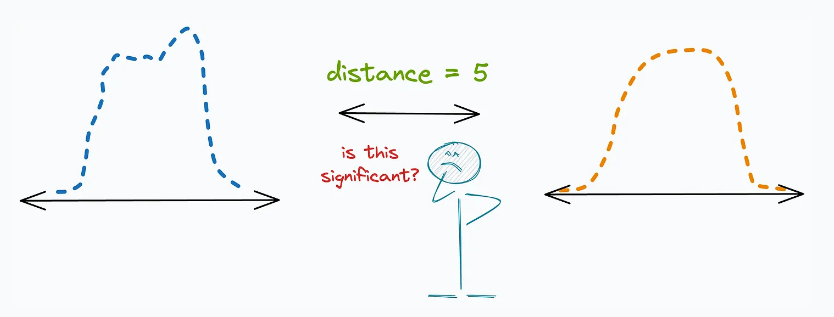
下面是一些常见的距离测量方法及其在测试正态性时的应用：

(1) "巴氏距离（Bhattacharyya distance）"的定义是：

• 测量两个分布之间的重叠，通常被解释为两个分布之间的接近程度。
• 选择与观察到的分布具有最小Bhattacharyya距离的参考分布，作为最接近的分布。

(2) 「海林格距离（Hellinger distance）」：

• 用于衡量两个分布之间的相似度，类似于Bhattacharyya距离。
• 与Bhattacharyya距离不同的是，Hellinger距离满足三角不等式，这使得它在一些情况下更为实用。

(3) "KL 散度（KL Divergence）"：

• 它本身并不是严格意义上的“距离度量”，但在测试正态性时可以用作衡量信息丢失的指标。
• 选择与观察到的分布具有最小KL散度的参考分布，作为最接近的分布。

运用这些距离测量方法，我们能够比对观测到的分布与多个参考分布之间的差异，进而更好地评估数据的正态性。通过找出与观察到的分布距离最短的参考分布，我们可以更精确地判断数据是否符合正态分布

Atas ialah kandungan terperinci 11 kaedah asas untuk menentukan kenormalan taburan data. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!