HTML5 기반의 3D 네트워크 토폴로지 트리 표현을 위한 그래픽 및 텍스트 코드에 대한 자세한 설명

HT for Web에서는 2D 및 3D 애플리케이션 모두 서로 다른 표시 효과로 트리 구조 데이터 표시를 지원합니다. 2D의 트리 구조는 분명한 계층 관계를 가지고 있지만 데이터의 양이 크면 직관적이지 않고 지정된 노드를 찾기가 더 어렵습니다. 그러나 HT for Web의 Elastic 레이아웃 구성 요소와 결합하면 3D의 트리 구조가 더 직관적으로 나타납니다. 대략적인 아이디어이지만 탄력적 레이아웃의 영향으로 계층 구조가 명확하지 않습니다. 그렇다면 이때, 구조가 명확한 3D 트리가 필요하게 됩니다. 그렇다면 이 3D 트리는 과연 어떤 모습일까요? 함께 보시죠~

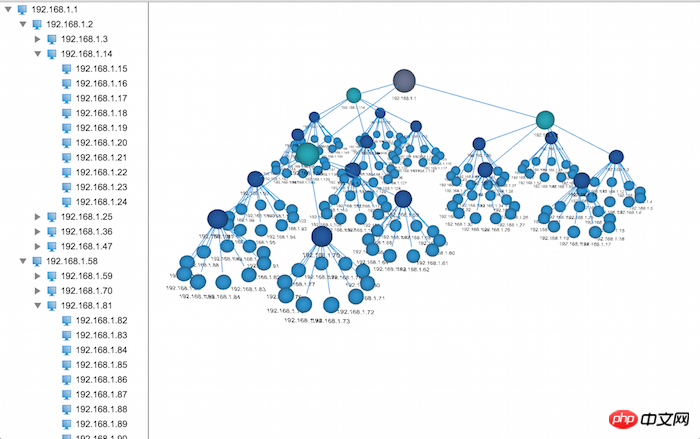
효과, 어디서부터 시작해야 할까? 다음으로, 이 문제를 해결해야 할 몇 가지 작은 문제로 나누어 보겠습니다.

1. 트리 구조 생성

웹용 HT를 배운 분들은 트리 구조 데이터 생성에 대해 잘 알고 계실 것이므로 여기서는 깊이 다루지 않겠습니다. 트리 구조 데이터 생성은 매우 간단합니다. 코드를 더욱 간결하게 만들기 위해 구체적인 코드는 다음과 같습니다.

/**
 * 创建连线
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} source - 起点
 * @param {ht.Node} target - 终点
 */
function createEdge(dataModel, source, target) {
    // 创建连线，链接父亲节点及孩子节点
    var edge = new ht.Edge();
    edge.setSource(source);
    edge.setTarget(target);
    dataModel.add(edge);
}

/**
 * 创建节点对象
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} [parent] - 父亲节点
 * @returns {ht.Node} 节点对象
 */
function createNode(dataModel, parent) {
    var node = new ht.Node();
    if (parent) {
        // 设置父亲节点
        node.setParent(parent);

        createEdge(dataModel, parent, node);
    }
    // 添加到数据容器中
    dataModel.add(node);
    return node;
}

/**
 * 创建结构树
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} parent - 父亲节点
 * @param {Number} level - 深度
 * @param {Array} count - 每层节点个数
 * @param {function(ht.Node, Number, Number)} callback - 回调函数(节点对象，节点对应的层级，节点在层级中的编号)
 */
function createTreeNodes(dataModel, parent, level, count, callback) {
    level--;
    var num = (typeof count === 'number' ? count : count[level]);

    while (num--) {
        var node = createNode(dataModel, parent);
        // 调用回调函数，用户可以在回调里面设置节点相关属性
        callback(node, level, num);
        if (level === 0) continue;
        // 递归调用创建孩子节点
        createTreeNodes(dataModel, node, level, count, callback);
    }
}

코드는 다음과 같습니다. 작성하기가 약간 복잡합니다. 간단한 방법은 여러 개의 for 루프를 중첩하여 트리 구조의 데이터를 만드는 것입니다. 다음으로 두 번째 질문을 살펴보겠습니다.

2. 2D 토폴로지에서 3D 트리 구조의 각 레이어의 반경 계산을 시뮬레이션합니다.

3D 트리 구조의 가장 큰 문제점은 각 노드의 레벨과 각 레이어 A 노드의 반경은 상위 노드를 중심으로 계산됩니다. 이제 트리 구조 데이터를 사용할 수 있으므로 반경 계산을 시작할 차례입니다. 2계층 트리 구조에서 시작합니다.

이제 계층 트리에서 두 개를 만듭니다. 구조에서 모든 하위 노드는 정렬되어 있으며 상위 노드를 둘러싸지 않습니다. 그러면 이러한 하위 노드의 위치를 ​​어떻게 결정합니까?

우선 각 끝 노드에는 자체 도메인의 원이 있다는 점을 알아야 합니다. 그렇지 않으면 노드 간에 겹침이 발생하므로 여기서는 끝 노드의 도메인 반경을 25로 가정합니다. 그러면 인접한 두 노드 사이의 최단 거리는 노드 필드 반경의 두 배인 50이 되며, 이 끝 노드는 부모 노드를 고르게 둘러싸게 됩니다. 그러면 인접한 두 노드의 열림 각도를 확인할 수 있습니다. 열림 각도로 나오세요. 두 점 사이의 거리, 부모 노드 주변의 노드의 최단 반경도 계산할 수 있습니다. 개방 각도가 a이고 두 점 사이의 최소 거리가 b이면 최소 반경 r이 계산 공식은 다음과 같습니다.

r = b / 2 / sin(a / 2);

그런 다음 코드는 다음과 같이 작성됩니다.

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 * @param {Number} [minR] - 末端节点的最小半径
 */
function layout(root, minR) {
    // 设置默认半径
    minR = (minR == null ? 25 : minR);
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = Math.PI * 2 / len;
    // 根据三角函数计算绕父亲节点的半径
    var sin = Math.sin(degree / 2),
        r = minR / sin;
    // 获取父亲节点的位置坐标
    var rootPosition = root.p();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            y = c * r;

        // 设置孩子节点的位置坐标
        child.p(x + rootPosition.x, y + rootPosition.y);
    });
}

, 기본적으로 끝 반경을 25로 설정했음을 알 수 있습니다. 이러한 방식으로 레이아웃() 메서드를 호출하여 구조 트리를 배치할 수 있습니다.

렌더링에서 볼 수 있듯이 끝 노드의 기본 반경은 그다지 이상적이지 않으므로 레이아웃 효과가 거의 보이지 않으므로 문제를 해결하기 위해 끝 노드의 기본 반경을 늘릴 수 있습니다. 너무 조밀한 레이아웃 문제, 예를 들어 기본 반경을 40으로 설정한 효과는 다음과 같습니다.

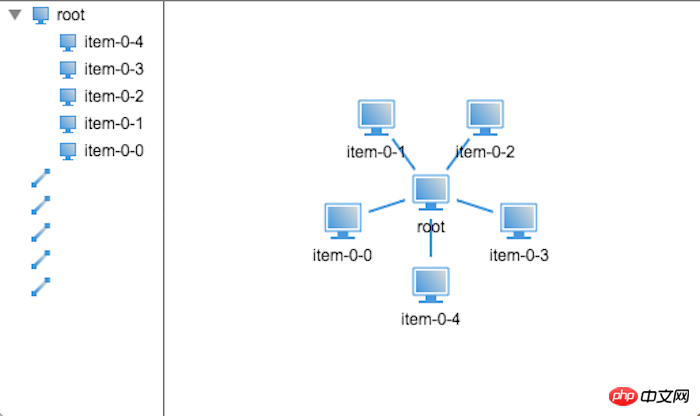
이제 2계층 트리 분포가 해결되었으므로 3계층 트리 분포를 다루는 방법을 살펴보세요.

두 번째 레이어와 세 번째 레이어를 전체적으로 고려하면 세 레이어의 트리 구조는 실제로 두 레이어의 트리 구조와 동일하지만 차이점은 두 번째 레이어 노드를 처리할 때 다음과 같아야 한다는 것입니다. 2계층 트리 구조를 처리하려면 재귀가 이러한 규칙성을 처리하는 가장 좋은 방법이므로 코드를 조금 시험해보고 어떻게 작동하는지 살펴보겠습니다.

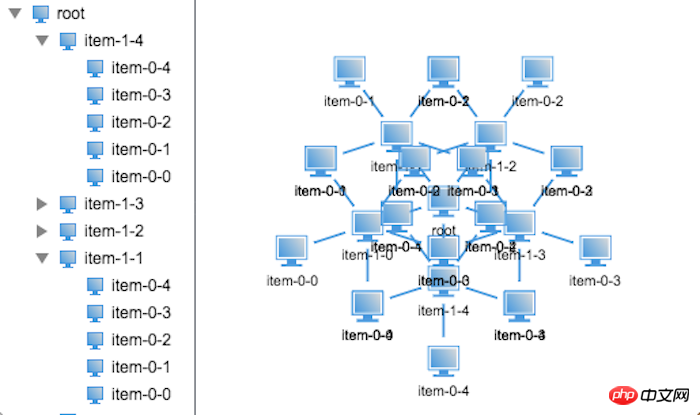
아니요, 노드가 모두 겹쳐져 있습니다. 단순 재귀는 작동하지 않을 것 같습니다. 그러면 구체적인 문제는 어디에 있습니까?

신중하게 분석한 결과, 아버지 노드의 도메인 반경은 자식 노드의 도메인 반경에 의해 결정되므로 레이아웃 시 자신의 노드의 도메인 반경과 위치를 알아야 합니다. 노드의 위치는 부모 노드의 반경과 위치 정보에 따라 달라지므로 반경을 계산하는 동안 노드 위치를 배치할 수 없습니다.

이제 레이아웃에서 반경 계산만 분리하고 2단계 작업을 수행할 수 있습니다. 먼저 노드 반경 계산을 분석해 보겠습니다.

먼저 해야 할 작업은 다음과 같습니다. 가장 중요한 조건을 명확히 하세요. 노드의 반경은 자식 노드의 반경에 따라 달라집니다. 이 조건은 노드 반경이 아래에서 위로만 계산될 수 있음을 알려줍니다. 따라서 우리가 설계하는 재귀 함수는 먼저 재귀적이어야 합니다. 그런 다음 더 이상 고민하지 말고 코드 구현을 살펴보겠습니다.

/**
 * 就按节点领域半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
    minR = (minR == null ? 25 : minR);

    // 若果是末端节点，则设置其半径为最小半径
    if (!root.hasChildren()) {
        root.a('radius', minR);
        return;
    }

    // 遍历孩子节点递归计算半径
    var children = root.getChildren();
    children.each(function(child) {
        countRadius(child, minR);
    });

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius');

    // 计算子节点的1/2张角
    var degree = Math.PI / children.size();
    // 计算父亲节点的半径
    var pRadius = radius / Math.sin(degree);

    // 设置父亲节点的半径及其孩子节点的布局张角
    root.a('radius', pRadius);
    root.a('degree', degree * 2);
}

OK，半径的计算解决了，那么接下来就该解决布局问题了，布局树状结构数据需要明确：孩子节点的坐标位置取决于其父亲节点的坐标位置，因此布局的递归方式和计算半径的递归方式不同，我们需要先布局父亲节点再递归布局孩子节点，具体看看代码吧：

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 */
function layout(root) {
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = root.a('degree');
    // 根据三角函数计算绕父亲节点的半径
    var r = root.a('radius');
    // 获取父亲节点的位置坐标
    var rootPosition = root.p();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            y = c * r;

        // 设置孩子节点的位置坐标
        child.p(x + rootPosition.x, y + rootPosition.y);

        // 递归调用布局孩子节点
        layout(child);
    });
}

代码写完了，接下来就是见证奇迹的时刻了，我们来看看效果图吧：

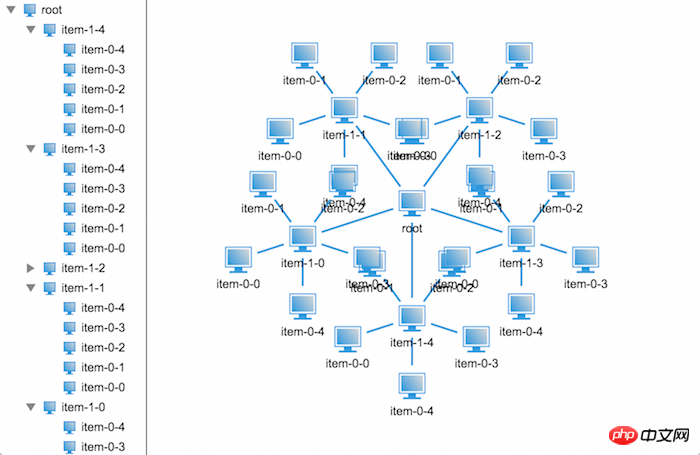
不对呀，代码应该是没问题的呀，为什么显示出来的效果还是会重叠呢？不过仔细观察我们可以发现相比上个版本的布局会好很多，至少这次只是末端节点重叠了，那么问题出在哪里呢？

不知道大家有没有发现，排除节点自身的大小，倒数第二层节点与节点之间的领域是相切的，那么也就是说节点的半径不仅和其孩子节点的半径有关，还与其孙子节点的半径有关，那我们把计算节点半径的方法改造下，将孙子节点的半径也考虑进去再看看效果如何，改造后的代码如下：

/**
 * 就按节点领域半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
   ……

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius');

    var child00 = child0.getChildAt(0);
    // 半径加上孙子节点半径，避免节点重叠
    if (child00) radius += child00.a('radius');

   ……
}

下面就来看看效果吧~

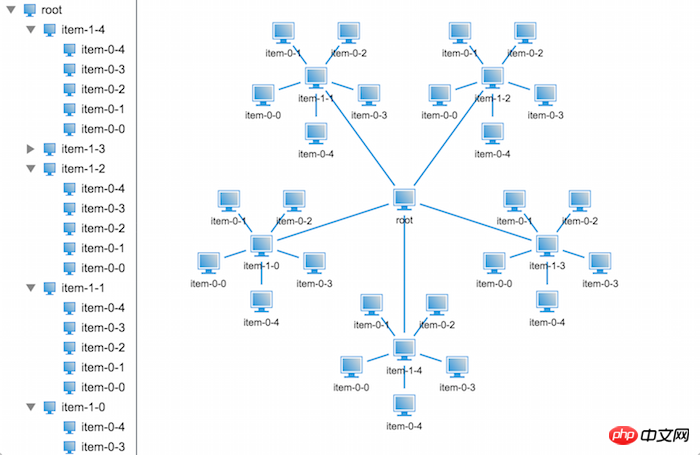
哈哈，看来我们分析对了，果然就不再重叠了，那我们来看看再多一层节点会是怎么样的壮观场景呢？

哦，NO！这不是我想看到的效果，又重叠了，好讨厌。

不要着急，我们再来仔细分析分析下，在前面，我们提到过一个名词——领域半径，什么是领域半径呢？很简单，就是可以容纳下自身及其所有孩子节点的最小半径，那么问题就来了，末端节点的领域半径为我们指定的最小半径，那么倒数第二层的领域半径是多少呢？并不是我们前面计算出来的半径，而应该加上末端节点自身的领域半径，因为它们之间存在着包含关系，子节点的领域必须包含于其父亲节点的领域中，那我们在看看上图，是不是感觉末端节点的领域被侵占了。那么我们前面计算出来的半径代表着什么呢？前面计算出来的半径其实代表着孩子节点的布局半径，在布局的时候是通过该半径来布局的。

OK，那我们来总结下，节点的领域半径是其下每层节点的布局半径之和，而布局半径需要根据其孩子节点个数及其领域半径共同决定。

好了，我们现在知道问题的所在了，那么我们的代码该如何去实现呢？接着往下看：

/**
 * 就按节点领域半径及布局半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
    minR = (minR == null ? 25 : minR);

    // 若果是末端节点，则设置其布局半径及领域半径为最小半径
    if (!root.hasChildren()) {
        root.a('radius', minR);
        root.a('totalRadius', minR);
        return;
    }

    // 遍历孩子节点递归计算半径
    var children = root.getChildren();
    children.each(function(child) {
        countRadius(child, minR);
    });

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius'),
        totalRadius = child0.a('totalRadius');

    // 计算子节点的1/2张角
    var degree = Math.PI / children.size();
    // 计算父亲节点的布局半径
    var pRadius = totalRadius / Math.sin(degree);

    // 缓存父亲节点的布局半径
    root.a('radius', pRadius);
    // 缓存父亲节点的领域半径
    root.a('totalRadius', pRadius + totalRadius);
    // 缓存其孩子节点的布局张角
    root.a('degree', degree * 2);
}

在代码中我们将节点的领域半径缓存起来，从下往上一层一层地叠加上去。接下来我们一起验证其正确性：

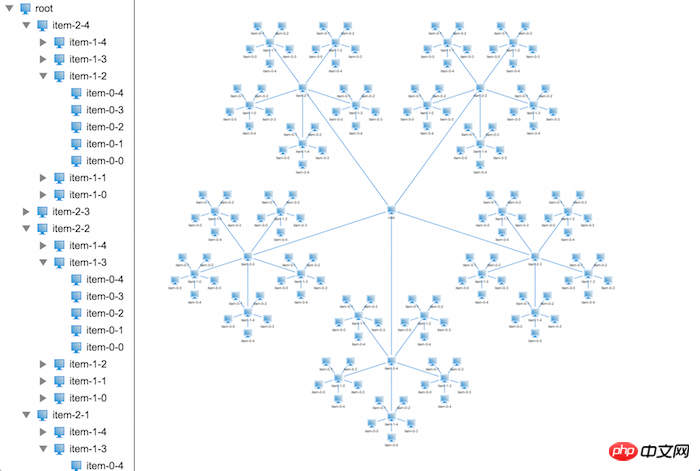
搞定，就是这样子了，2D拓扑上面的布局搞定了，那么接下来该出动3D拓扑啦~

3. 加入z轴坐标，呈现3D下的树状结构

3D拓扑上面布局无非就是多加了一个坐标系，而且这个坐标系只是控制节点的高度而已，并不会影响到节点之间的重叠，所以接下来我们来改造下我们的程序，让其能够在3D上正常布局。

也不需要太大的改造，我们只需要修改下布局器并且将2D拓扑组件改成3D拓扑组件就可以了。

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 */
function layout(root) {
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = root.a('degree');
    // 根据三角函数计算绕父亲节点的半径
    var r = root.a('radius');
    // 获取父亲节点的位置坐标
    var rootPosition = root.p3();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            z = c * r;

        // 设置孩子节点的位置坐标
        child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);

        // 递归调用布局孩子节点
        layout(child);
    });
}

上面是改造成3D布局后的布局器代码，你会发现和2D的布局器代码就差一个坐标系的的计算，其他的都一样，看下在3D上布局的效果：

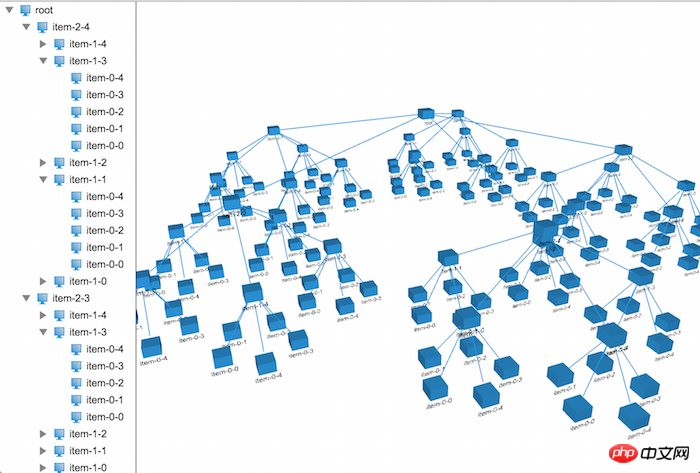
恩，有模有样的了，在文章的开头，我们可以看到每一层的节点都有不同的颜色及大小，这些都是比较简单，在这里我就不做深入的讲解，具体的代码实现如下：

var level = 4,
    size = (level + 1) * 20;

var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);

root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);

var colors = {},
    sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
    if (!colors[level]) {
        colors[level] = randomColor();
        sizes[level] = (level + 1) * 20;
    }

    size = sizes[level];

    data.setName('item-' + level + '-' + num);
    // 设置节点形状为球形
    data.s('shape3d', 'sphere');
    data.s('shape3d.color', colors[level]);
    data.s3(size, size, size);
});

在这里引入了一个随机生成颜色值的方法，对每一层随机生成一种颜色，并将节点的形状改成了球形，让页面看起来美观些（其实很丑）。

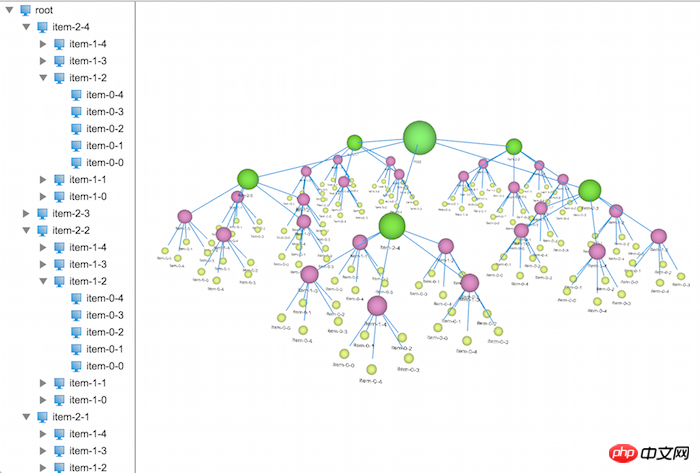
提个外话，节点上可以贴上图片，还可以设置文字的朝向，可以根据用户的视角动态调整位置，等等一系列的拓展，这些大家都可以去尝试，相信都可以做出一个很漂亮的3D树出来。

到此，整个Demo的制作就结束了，今天的篇幅有些长，感谢大家的耐心阅读，在设计上或则是表达上有什么建议或意见欢迎大家提出，点击这里可以访问HT for Web官网上的手册。

위 내용은 HTML5 기반의 3D 네트워크 토폴로지 트리의 그래픽 코드에 대한 자세한 설명입니다. 더 많은 관련 내용은 PHP 중국어 홈페이지(www.php.cn)를 참고해주세요!