캔버스 실제 사례 2 - 부채꼴 모양

씨앗을 남기지 않고 사진을 올리면 수천명이 국화를 찔러간다는 속담! 나는 이것을 좀 더 확장하고 싶습니다. 가르칠 때 모범을 보이지 않으면 바보라고 불릴 것입니다! 아, 운율이 많이 맞는데, 헤헤, 농담이에요!

우리는 API에 대한 지식을 네 가지 주제로 이야기했습니다. 아마도 모두에게 매우 지루할 것입니다. 이전의 작은 예는 너무 간단하고 갈증을 해소하지 못합니다. 숨. , 마음을 상쾌하게 하기 위해 아래에 작은 예를 들어보겠습니다!
앞서 원을 그리는 이야기를 했을 때 부채꼴 모양을 어떻게 그리는지에 대한 생각, 혹은 함정이 있었나요? 원을 그리는 방법은 한 번에 섹터를 그릴 수 없다는 것을 알고 있습니다. 그 방법을 제가 제공한 것입니다. 인상이 없으셔도 상관은 없습니다. 다시 말하지만, 호를 그리면 원의 중심에 두 개의 선을 그려 호의 시작점과 끝점을 각각 연결합니다. 그러면 이것은 원이 아닌가요? 그러면 이 방법으로 원을 그릴 수 있나요? 사실 잘 모르겠으니 한번 해보자:
첫 번째 단계는 호를 그리는 것이다:

//将原点移到100,100的位置
ctx.translate(100, 100);
//画一个圆弧
ctx.arc(0,0,100,30*Math.PI/180, 60*Math.PI/180);
ctx.stroke();

이것이 우리다 이제 호를 그리는 친숙한 방법을 살펴보겠습니다. 이것이 바로 핵심입니다. 칼을 갈는 데는 나무를 자를 필요가 없습니다.

직선은 2개의 점으로 구성됩니다. 이제 원의 중심을 알았으니 두 번째 점이 호의 시작점과 끝점입니다. 그렇다면 이 두 점의 좌표는 어떻게 구할까요? ? 분석하기 위해 그림을 그려 봅시다.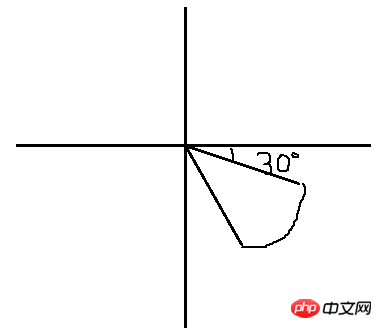



우리는 아마도 이런 부채꼴 모양을 그리고 싶을 것입니다. 그것은 다소 보기 흉합니다. 그리고 각도 공식을 이용하세요. 1. 일반적인 계산을 통해 이 두 점의 좌표를 구할 수도 있지만, 제가 수학을 잘 못해서 이 계산이 얼마나 중복됐는지 생각이 듭니다. 계산을 안하고도 쉽게 할 수 있는 방법이 있나요? (죄송합니다. 내 "기억"은 분명히 부족합니다.) 나는 부채 모양이 이렇게 기울어지지 않고 한쪽이 수평이라면 예를 들어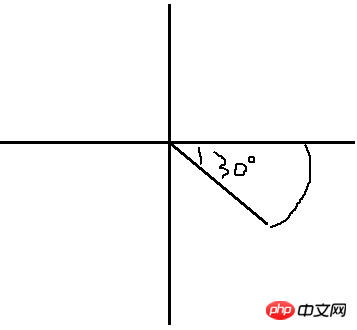




그러면 첫 번째 선분, 즉 가로좌표의 선분을 쉽게 구할 수 있는 것 아시죠? 좋아요, 이렇습니다. 원의 중심 좌표와 반지름을 알고 나면 호의 시작점 좌표를 아는 것이 매우 쉽습니다. 다른 선을 어떻게 구하나요? 지난 호의 API 지식을 방금 읽었다면 아직 뜨거울 때 Rotate() 메서드를 쉽게 생각할 수 있습니다. 즉, 원의 중심에서 시작점까지 또 다른 선을 그립니다. 우리는 호의 각도를 알고 있습니다. 좋습니다. 새로 그린 선의 호의 각도를 선택하면 끝점에 도달하지 않을까요? 젠장, 난 정말 똑똑해! 시도해 봅시다:

//圆弧
ctx.save();
ctx.translate(100, 100);
ctx.arc(0,0,100,0, 30*Math.PI/180);
ctx.restore();
//第一条线
ctx.save();
ctx.moveTo(100,100);
ctx.lineTo(200,100);
ctx.restore();
//第二条线
ctx.save();
ctx.translate(100, 100);
ctx.moveTo(0,0);
ctx.rotate(30*Math.PI/180);
ctx.lineTo(100,0);
ctx.stroke();
ctx.restore();

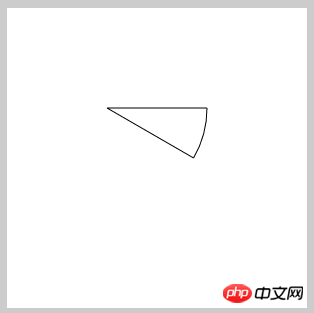
와, 정말 놀랍습니다. 이 아이디어에 따르면, 지금 이 부문이 바뀌고 있습니다. 각도로, 그리고 이 각도 = 두 번째 선의 각도 - 첫 번째 선의 각도, 그러면 우리가 얻는 것이 우리에게 필요한 섹터가 아닌가요? 그러나 이전 코드의 직접 회전은 선이 아닌 호만 회전할 수 있습니다. 수정해 보겠습니다.




이 그림을 보면 생각이 바뀔 수 있습니다. , 목표 위치에 호를 그리면 각도가 0인 선 2개를 그린 후 호의 시작점과 끝점으로 회전하면 충분하지 않을까요? (호의 시작 각도와 끝 각도를 알고 있기 때문에) 시도해 보세요:

//将原点设置100,100位置
ctx.translate(100,100);
//原点在100,100，则圆心设为0,0 ——> 100,100的位置
ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180);
//save(),restore()是为了防止角度旋转的污染
ctx.save();
ctx.rotate(30*Math.PI/180);
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.restore();
ctx.rotate(60*Math.PI/180);
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.stroke();

哎呀，真的可以啊，哈哈，有人会问，你的第一步为什么是设置原点呢，为什么不用moveTo来设置起始点呢？好问题，因为画布的默认原点在0,0的位置上，如果用moveTo来设置起始点，原点依然还在0,0的位置，上一节API我们将变换的时候讲到，变换是以原点为基准点的，即使你设置了起始点，但是起始点不是原点的话，图形旋转依然会围绕0,0点旋转然后自转，得到的图形就不知道是什么图形了，偏差的角度就很难矫正，对此还是不太明白的同学可以自己写一个例子体验一样，或许理解更深刻一点，这里就作为练习题，不在这里写了！

上面的代码还是可以优化的，比如说画第一条线的时候，我们用到了save()和restore()，其作用不只是可以防止外面的属性或方法对里面的绘制产生影响，它的本质意思是save()保存当前环境的状态，restore()返回之前保存路径的状态，这是什么意思，举个栗子，save()就像是在一个迷宫的入口，restore()就想是这个迷宫的出口，但是发现这里就是迷宫的路口，出了迷宫，在迷宫里具体是怎么走的，根本不知道，这就可以防止你的外部因素来影响你走迷宫的路线，那有一个细节大家要注意，就是当你进去的这个门，你出来的时候还是这个门，恩，这个就可以利用了，这就相当于是画笔的触点了，还原触点，我们看一下还原的触点在什么地方：

//将原点设置100,100位置
ctx.translate(100,100);
//原点在100,100，则圆心设为0,0 ——> 100,100的位置
ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180);
//save(),restore()是为了防止角度旋转的污染
ctx.save();
ctx.rotate(30*Math.PI/180);
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.restore();
ctx.rotate(60*Math.PI/180);
ctx.lineTo(100,0);
ctx.stroke();

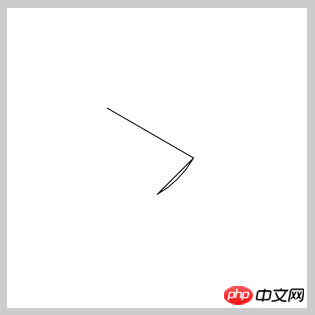
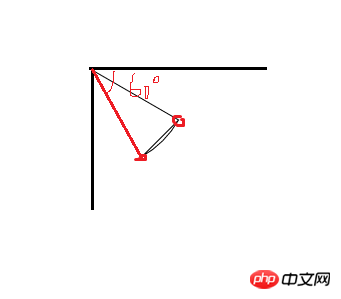
居然得到的是这样的结果，从第2张图可以看出还原的触点的位置在圆弧的初始点，其实这里我们是忽略了一个问题，就是线在旋转的时候，是从它的起点为圆心旋转的，而上面的代码是，第一条线从圆心开始，到圆弧的起点（旋转过后），自然现在的起点就是圆弧的起点了，第二条线怎么画，它旋转的结果都不是我们想要的了，所以这里我们需要特别的注意，现在我们将第一条直线的起点设在（r,0）的位置，旋转后就到了圆弧的起始点，然后在画到圆心地方，那现在的起始点就是圆心了，再画一条线到圆弧，就哦了，现在我们再来一次：

//将原点设置100,100位置
ctx.translate(100,100);
//原点在100,100，则圆心设为0,0 ——> 100,100的位置
ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180);
//save(),restore()是为了防止角度旋转的污染
ctx.save();
ctx.rotate(30*Math.PI/180);
ctx.moveTo(100,0);
ctx.lineTo(0,0);
ctx.restore();
ctx.rotate(60*Math.PI/180);
ctx.lineTo(100,0);
ctx.stroke();

看，这就是我们想要的图形，所以，上面所犯的几个错都是比较容易犯的错，需要特别的注意！

根据这个原理，我们其实还可以用另外一种方式，就是充分使用触点的作用，怎么讲，当我们再画圆弧的时候，画完之后其触点在圆弧的结束位置，如此的天赐良机，为何不直接将这个触点作为起点，画一条到圆心的线，不就可以少旋转一次吗？然后再画第二条线，简直感觉省时省力，我们看看效果吧：

//将原点设置100,100位置
ctx.translate(100,100);
//原点在100,100，则圆心设为0,0 ——> 100,100的位置
ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180);
//以圆弧终点为起点画直线
ctx.lineTo(0,0);
ctx.rotate(30*Math.PI/180);
//以0,0为起点画直线
ctx.lineTo(100,0);
ctx.stroke();

你看，用这个理论，就连save(),restore()都可以省了，因为就只有一个旋转，代码也少了好多，效果还一样，哈哈，为了能重复使用，我们需要把他封装一下：

第一种：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
            this.save();
            this.translate(x,y);
            this.beginPath();
            this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
            this.save();
            this.rotate(sDeg*Math.PI/180);
            this.moveTo(r,0);
            this.lineTo(0,0);
            this.restore();
            this.rotate(eDeg*Math.PI/180);
            this.lineTo(r,0);
            this.restore();
            return this;
        }
        ctx.sector(100,100,100,30,60).stroke();
        ctx.sector(100,100,100,90,120).fill();
        ctx.sector(100,100,100,160,180).stroke();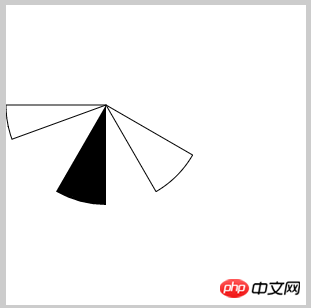

第二种：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
            this.save();
            this.translate(x,y);
            this.beginPath();
            this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
            this.lineTo(0,0);
            this.rotate(sDeg*Math.PI/180);
            this.lineTo(r,0);
            this.restore();
            return this;
        }
        ctx.sector(100,100,100,30,60).stroke();
        ctx.sector(100,100,100,90,120).fill();
        ctx.sector(100,100,100,160,180).stroke();

你以为这样就完了吗？当我们充分理解canvasAPI的基础知识的时候，我们还会得到另外一种方式来画扇形，简直6到爆！哈哈哈！究竟是什么呢？我们接着往下看：

前面的基础知识讲到画圆的时候，我们讲到了beginPath()和closePath()，有人会说，这不就是开始路径和封闭路径吗？这跟画扇形有什么关系？没错，你说的一点都没错，好，现在请大声跟我念：封闭路径！封闭路径！封闭路径！重要事情说3遍，现在你的心里是不是有了那么一点感觉，没错，不要觉得害羞，不要觉得压抑，就是它，就是它，大声把它说出来，就是这感觉，什么？你什么感觉都没有，此处有表情，好吧，我来告诉你我的感觉：

上面有一处说，为什么要用translate，而不要moveTo，是因为我们需要旋转，所以就需要原点，现在如果我们不需要旋转，而是正常的画图，那么我们就不需要原点，我们就可以用moveTo，好了，如果我们配合beginPath()和closePath()，就会将一个圆弧封闭起来，想想我们在讲画三角形的时候的那段折线是怎么变成三角形的，没错，现在是否有了一点感觉？还是木有？好吧，我们来看一个栗子：

ctx.beginPath();
//定义起点
ctx.moveTo(100,100);
//以起点为圆心，画一个半径为100的圆弧
ctx.arc(100,100,100,30*Math.PI/180, 60*Math.PI/180);
ctx.closePath();
ctx.stroke();

看看，寥寥数行，就画出了一个扇形，对不上面的图像，是不是一样的？我们封装一下：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
            this.save();
            this.beginPath();
            this.moveTo(x,y);
            this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
            this.closePath();    
            this.restore();
            return this;
        }
        ctx.sector(100,100,100,30,60).stroke();
        ctx.sector(100,100,100,90,120).fill();
        ctx.sector(100,100,100,160,180).stroke();

效果都一样，只是思路不一样，或许还有别的方式来画扇形，如果大家有更好的方法，希望能留下你的代码，大家互相学习一下！

扇形的方法有了，具体用哪个可以依据自己的喜好，我就按照第3种来写一个小应用，饼图：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
            this.save();
            this.beginPath();
            this.moveTo(x,y);
            this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
            this.closePath();    
            this.restore();
            return this;
        }
        ctx.fillStyle = 'red';
        ctx.sector(200,200,100,30,150).fill();
        ctx.fillStyle = 'green';
        ctx.sector(200,200,100,150,270).fill();
        ctx.fillStyle = 'blue';
        ctx.sector(200,200,100,270,390).fill();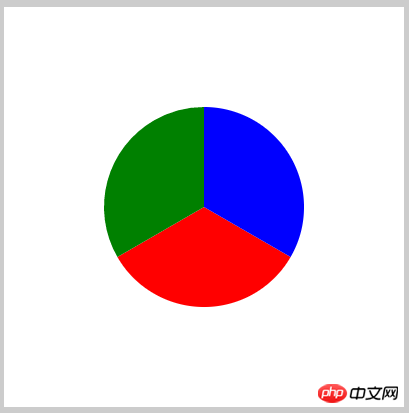

再写一个扇形倒计时：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
            this.save();
            this.beginPath();
            this.moveTo(x,y);
            this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
            this.closePath();    
            this.restore();
            return this;
        }
        
        var angle = 0;
        var timer = null;
        ctx.fillStyle = 'green';
        setInterval(function(){
            angle+=5;
            ctx.sector(200,200,100,0,angle).fill();
            if(angle == 360){
                clearInterval(timer);  
            }
        },200);

你以为我只是写几个例子给你看吗？你还是太年轻了，之所以要丢出这2个例子，是为了扩展一下思路，我们可以在这些效果上面加一点什么东西，效果是否就不一样了，举个例子，第一个饼图，如果我们在中间加一个白色的圆，会怎么样？

CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
            this.save();
            this.beginPath();
            this.moveTo(x,y);
            this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
            this.closePath();    
            this.restore();
            return this;
        }
        ctx.fillStyle = 'red';
        ctx.sector(200,200,100,30,150).fill();
        ctx.fillStyle = 'green';
        ctx.sector(200,200,100,150,270).fill();
        ctx.fillStyle = 'blue';
        ctx.sector(200,200,100,270,390).fill();
        ctx.fillStyle = '#fff';
        ctx.sector(200,200,80,0,360).fill();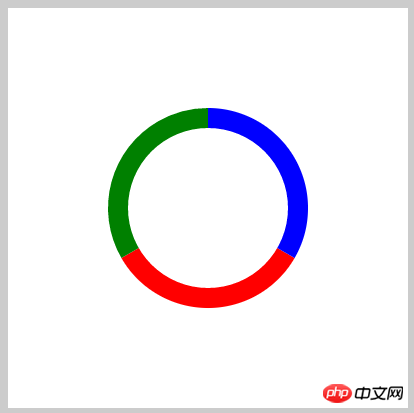

看，这效果是不是就变成另外一个效果了，比如说第二个效果，我们也加一个白色的圆，看有什么效果：

CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
            this.save();
            this.beginPath();
            this.moveTo(x,y);
            this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
            this.closePath();    
            this.restore();
            return this;
        }

        var angle = 0;
        var timer = null;
        setInterval(function(){
            angle+=5;
            ctx.fillStyle = 'green';
            ctx.sector(200,200,100,0,angle).fill();
            ctx.fillStyle = '#fff';
            ctx.sector(200,200,80,0,360).fill();
            if(angle == 360){
                clearInterval(timer);    
            }
            
        },200);

看看，这效果是不是可以做很多的效果，当然，因为没有加动画效果，现在的效果很生硬，需要大家来完善，只要你脑洞打开，其实扇形还是能做出很多非常炫酷的效果的，当然了，好的效果都是需要打磨的，在此只是抛砖引玉，如果大家有更好，更炫酷的效果，请不吝分享一下，今天就讲到这里，谢谢大家的支持！

 以上就是canvas实践小实例二  —— 扇形 的内容，更多相关内容请关注PHP中文网（www.php.cn）！