Implémenter l'interpolation bilinéaire et l'interpolation bicubique en js

Recommandation d'apprentissage gratuite : Tutoriel vidéo js

• Introduction
• Interpolation bilinéaire
• • Principe
• Interpolation bicubique
• • Principe
• Implémentation js

Introduction

Lors de l'utilisation de Canvas pour dessiner sur une page Web, j'ai rencontré un problème, original La résolution des données est très petit et l'image doit être agrandie sur toute la page Web, les données doivent donc être agrandies par interpolation. J'ai appris l'interpolation bilinéaire et l'interpolation cubique. Les deux méthodes ont des effets différents. Elles sont toutes deux implémentées avec du code js. Permettez-moi de partager avec vous

Interpolation bilinéaire

Principe

L'interpolation bilinéaire consiste à effectuer une interpolation linéaire sur les données dans chacune des directions x et y.

La matrice des données originales, c'est-à-dire un tableau bidimensionnel, la taille est a*b, la taille de la matrice cible est m*n, m, n peut être plus grand (agrandi) ou plus petit (réduit) que a, b, bien sûr, le rapport. Il peut également être différent, en fonction de la taille de vos données interpolées.
L'idée de base est de parcourir les coordonnées de la matrice cible, comme le point x*y, de trouver la position correspondante de ce point dans la matrice d'origine, appelée point de cartographie, puis de trouver les quatre cartographies environnantes. point P dans le point de la matrice d'origine, puis effectuez deux fois une interpolation linéaire en fonction de la distance entre le point de cartographie P et les coordonnées dans les directions x et y des quatre points pour obtenir la valeur du point de cartographie.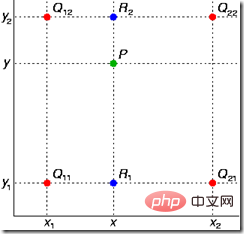

Comme le montre la figure ci-dessus, le point p est la position où le point x*y dans la matrice cible est cartographié dans la matrice d'origine. Les quatre points les plus proches autour de lui sont Q12, Q11. , Q21 et Q22. Maintenant x Une interpolation linéaire est effectuée dans la direction y pour obtenir les valeurs des deux points R1 et R2, puis une interpolation linéaire est effectuée dans la direction y pour obtenir la valeur du point P.
Remarque : après avoir utilisé l'interpolation bilinéaire pour amplifier les données, si le grossissement est trop grand, il y aura un phénomène de mosaïque évident après la génération de l'image
Veuillez vous référer au code js suivant pour le code d'implémentation

Méthode d'interpolation bicubique

Principe

L'interpolation bicubique est également appelée interpolation par convolution cubique. L'interpolation par convolution cubique est une méthode d'interpolation plus complexe. Cet algorithme utilise la valeur de gris de 16 points autour du point à échantillonner pour l'interpolation cubique, en tenant compte non seulement de l'influence du gris des quatre points directement adjacents, mais également de l'influence du taux de changement de la valeur de gris entre les points adjacents. Pour le principe spécifique, veuillez vous référer au blog suivant :

Référez-vous au blog ici
Le principe de base est de trouver d'abord le point de cartographie P du milieu de la matrice cible dans la matrice de données source, puis de trouver les 16 points autour du point P, puis selon P. La distance entre les coordonnées du point et les 16 points dans les directions x et y est utilisée pour calculer le poids de chaque point à l'aide de la fonction BiCubic. Enfin, après avoir multiplié chaque point par le poids, la valeur de P peut être obtenue en additionnant.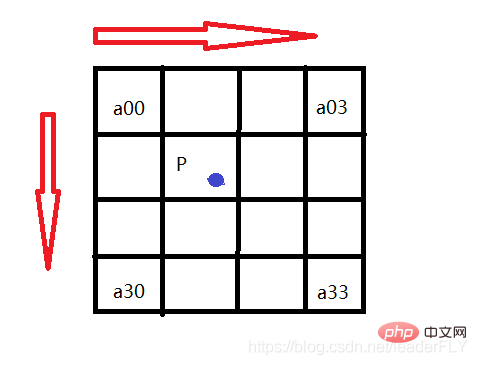

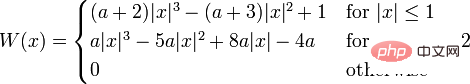Fonction BiCubic :

Parmi elles, lorsque a vaut -0,5, la fonction BiCubic a la forme suivante :

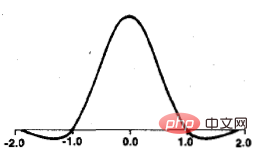Prenez a= À -0,5, les données agrandies sont assez bonnes, l'image générée est très fluide et conserve beaucoup de détails.
Je n'ai pas étudié en profondeur pourquoi cette fonction est utilisée, mais après avoir utilisé cette méthode pour amplifier les données, l'effet d'image généré est très bon, sans phénomène de mosaïque

Implémentation JS

/**
 * 数据处理工具类（也可以自己直接定义方法，不用class）
 */class DataUtil {
	constructor() {}}/**
 * 数据插值
 * @param w 目标矩阵宽度
 * @param h 目标矩阵高度
 * @param data 源数据矩阵（二维数组）
 * @param type 插值方式，1：双线性插值，2：双三次插值法
 */DataUtil.scaleData = function(w, h, data, type = 2) {
	let t1 = new Date().getTime();
	let dw = data[0].length;
	let dh = data.length;
	
	let resData = new Array(h);
	
	for (let j = 0; j  h - 1 ? h - 1 : py;
		for (let i = 0; i  w - 1 ? w - 1 : px;
			// 该点的值
			let dv = data[py][px];
			// 该点的权重
			let w_x = wx[i];
			let w_y = wy[j];
			// 根据加权加起来
			val += (dv * w_x * w_y);
		}
	}
	
	return val;}/**
 * 双三次插值法中，基于BiCubic基函数，计算源坐标v，最近的4*4的坐标和坐标对应的权重
 * @param v 目标矩阵中坐标对应在源矩阵中坐标值
 */DataUtil.getCubicWeight = function (v){
	let a = -0.5;
	
	// 取整
	let nv = Math.floor(v);
	
	// 坐标差值集合
	let xList = new Array(4);
	// 坐标集合
	let xs = new Array(4);
	
	// 最近的4个坐标差值
	xList[0] = nv - v - 1;
	xList[1] = nv - v
	xList[2] = nv - v + 1;
	xList[3] = nv - v + 2;
	// 
	xs[0] = nv - 1;
	xs[1] = nv;
	xs[2] = nv + 1;
	xs[3] = nv + 2;
	
	// 计算权重
	let ws = new Array(4);
	for (let i = 0; i <p>Recommandations d'apprentissage gratuites associées : <strong></strong><a href="https://www.php.cn/course/list/17.html" target="_blank" textvalue="javascript">javascript<strong></strong></a> (vidéo) <strong></strong></p>

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!