
The derivation chain rule is one of the important mathematical tools in machine learning. It is widely used in algorithms such as linear regression, logistic regression, and neural networks. This rule is an application of the chain rule in calculus and helps us calculate the derivative of a function with respect to a variable.
The composite function f(x) consists of multiple simple functions, each of which has a derivative with respect to x. According to the chain rule, the derivative of f(x) with respect to x can be obtained by multiplying and adding the derivatives of simple functions.
The formal expression is: if y=f(u) and u=g(x), then the derivative of y with respect to x dy/dx=f'(u)*g '(x).
This formula shows that by knowing the derivatives of simple functions with respect to x and how they are combined, we can calculate the derivatives of composite functions with respect to x.
The derivation chain rule plays a key role in optimization algorithms, especially in optimization algorithms such as gradient descent. It is used to update model parameters to minimize the loss function. The core idea of the chain rule is that if a function is composed of multiple simple functions, then the derivative of this function with respect to a variable can be obtained by multiplying the derivatives of each simple function with respect to the variable. In machine learning, this rule is widely used to calculate the gradient of the loss function with respect to the model parameters. The effectiveness of this approach allows us to efficiently train deep neural networks via the backpropagation algorithm.
In machine learning, we often need to optimize parameters, which involves solving the derivative of the loss function with respect to the parameters. The loss function is usually a composite function composed of multiple simple functions, so we need to use the chain rule to calculate the derivative of the loss function with respect to the parameters.
Suppose we have a simple linear regression model. The output y of the model is a linear combination of the input x, that is, y=Wx b, where W and b are the parameters of the model. If we have a loss function L(y,t), where t is the true label, we can calculate the gradient of the loss function with respect to the model parameters via the chain rule:
dL/dW= dL/dy*dy/dW
##dL/db=dL/dy*dy/db where dL/dy is the loss function Derivatives of the output, dy/dW and dy/db are the derivatives of the model’s output with respect to the parameters. Through this formula, we can calculate the gradient of the loss function on the model parameters, and then use optimization algorithms such as gradient descent to update the parameters of the model to minimize the loss function. In more complex models, such as neural networks, the chain rule is also widely used. Neural networks usually consist of multiple nonlinear and linear layers, each with its own parameters. In order to optimize the parameters of the model to minimize the loss function, we need to calculate the gradient of the loss function for each parameter using the chain rule. In short, the derivation chain rule is one of the very important mathematical tools in machine learning. It can help us calculate the derivative of a composite function with respect to a certain variable, and then use it to optimize the model. parameters to minimize the loss function.The above is the detailed content of Chain derivation rule in machine learning. For more information, please follow other related articles on the PHP Chinese website!
 7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AM
7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AMGenerative AI, exemplified by chatbots like ChatGPT, offers project managers powerful tools to streamline workflows and ensure projects stay on schedule and within budget. However, effective use hinges on crafting the right prompts. Precise, detail
 Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AM
Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AMThe challenge of defining Artificial General Intelligence (AGI) is significant. Claims of AGI progress often lack a clear benchmark, with definitions tailored to fit pre-determined research directions. This article explores a novel approach to defin
 IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AM
IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AMIBM Watsonx.data: Streamlining the Enterprise AI Data Stack IBM positions watsonx.data as a pivotal platform for enterprises aiming to accelerate the delivery of precise and scalable generative AI solutions. This is achieved by simplifying the compl
 The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AM
The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AMThe rapid advancements in robotics, fueled by breakthroughs in AI and materials science, are poised to usher in a new era of humanoid robots. For years, industrial automation has been the primary focus, but the capabilities of robots are rapidly exp
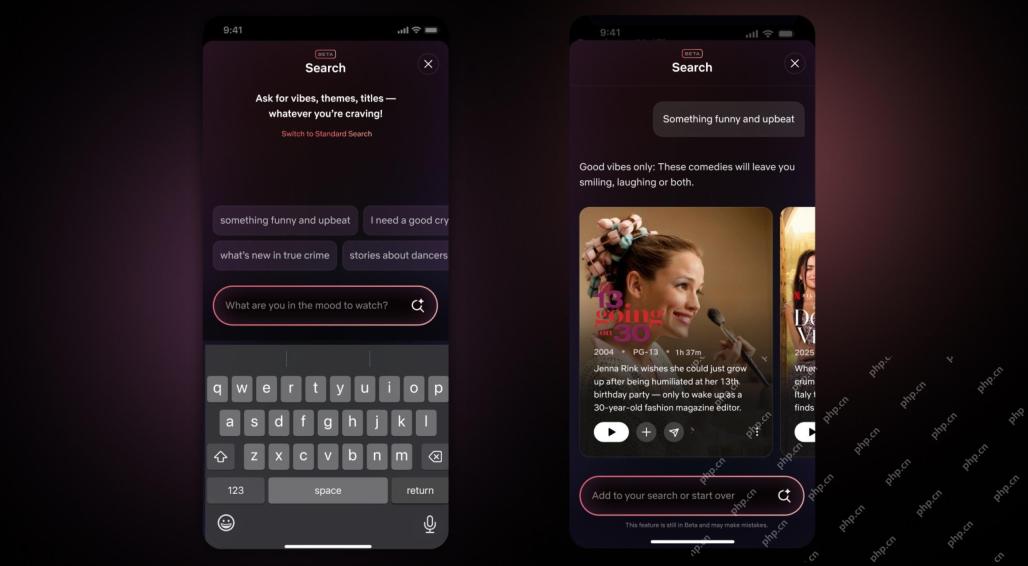 Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AM
Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AMThe biggest update of Netflix interface in a decade: smarter, more personalized, embracing diverse content Netflix announced its largest revamp of its user interface in a decade, not only a new look, but also adds more information about each show, and introduces smarter AI search tools that can understand vague concepts such as "ambient" and more flexible structures to better demonstrate the company's interest in emerging video games, live events, sports events and other new types of content. To keep up with the trend, the new vertical video component on mobile will make it easier for fans to scroll through trailers and clips, watch the full show or share content with others. This reminds you of the infinite scrolling and very successful short video website Ti
 Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AM
Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AMThe growing discussion of general intelligence (AGI) in artificial intelligence has prompted many to think about what happens when artificial intelligence surpasses human intelligence. Whether this moment is close or far away depends on who you ask, but I don’t think it’s the most important milestone we should focus on. Which earlier AI milestones will affect everyone? What milestones have been achieved? Here are three things I think have happened. Artificial intelligence surpasses human weaknesses In the 2022 movie "Social Dilemma", Tristan Harris of the Center for Humane Technology pointed out that artificial intelligence has surpassed human weaknesses. What does this mean? This means that artificial intelligence has been able to use humans
 Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AM
Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AMTransUnion's CTO, Ranganath Achanta, spearheaded a significant technological transformation since joining the company following its Neustar acquisition in late 2021. His leadership of over 7,000 associates across various departments has focused on u
 When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AM
When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AMBuilding trust is paramount for successful AI adoption in business. This is especially true given the human element within business processes. Employees, like anyone else, harbor concerns about AI and its implementation. Deloitte researchers are sc


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.






