Explore the concepts of Bayesian methods and Bayesian networks in depth

The concept of Bayesian method
The Bayesian method is a statistical inference theorem, mainly used in the field of machine learning. It performs tasks such as parameter estimation, model selection, model averaging and prediction by combining prior knowledge with observation data. Bayesian methods are unique in their ability to flexibly handle uncertainty and improve the learning process by continuously updating prior knowledge. This method is particularly effective when dealing with small sample problems and complex models, and can provide more accurate and robust inference results.
Bayesian methods are based on Bayes' theorem, which states that the probability of a hypothesis given some evidence is equal to the probability of the evidence multiplied by the prior probability.
This can be written as:
P(H|E)=P(E|H)P(H)
Where P(H|E) is the posterior probability of hypothesis H given evidence E, and P(E|H) is the possibility of observing evidence if H is true. property, P(H) is the probability of the prior probability hypothesis H. Posterior probabilities are updated based on new evidence and reflect our updated beliefs about the hypothesis. Prior probabilities are our initial beliefs about a hypothesis before any evidence is considered. Likelihood is a function of the likelihood of observing evidence if a hypothesis is true.
What are the advantages and disadvantages of using Bayesian methods
There are many benefits of using Bayesian methods, especially in machine learning.
1. Bayesian methods help avoid overfitting because they allow prior knowledge about the data to be integrated into the learning process.
2. Bayesian methods can be used to estimate uncertainty, which is important for making decisions based on data.
3. Bayesian methods can be used to compare different models and select the best model for a specific problem.
4. Bayesian methods can be used to conduct sensitivity analysis, which helps to understand the sensitivity of the model to different inputs.
5. Bayesian methods are generally more robust than other methods because they are less affected by outliers.
There are also some disadvantages to using Bayesian methods. First, Bayesian methods are computationally intensive because they require many iterations to update beliefs based on new evidence. Second, Bayesian methods can be difficult to implement because they require a good understanding of probability and statistics. Finally, Bayesian methods can be difficult to interpret because they often involve complex mathematical equations.
Definition of Bayesian Network
Bayesian network is a graphical model that models the probabilities between variables of interest Relationships are coded. Bayesian networks are well suited for representing and reasoning about complex domains characterized by uncertain conditions and hidden information. Bayesian networks can be used for a variety of tasks in machine learning, including classification, regression, and clustering. Bayesian networks are also used for dimensionality reduction, feature selection, and model selection.
Bayesian networks rely on a technique called probabilistic inference to answer questions about the probability of an event occurring given conditions. In a Bayesian network, nodes represent variables of interest and edges represent probabilistic relationships between these variables. The strength of the relationship is represented by conditional probabilities.
What are the advantages and disadvantages of using Bayesian networks
Compared with other methods of representing and reasoning about uncertainty, Bayesian Networking has many advantages. First, they can represent causal relationships between variables, which is important for understanding how changes in one variable affect another. Second, they can handle hidden variables, which is important for accurate predictions in domains where not all information is known or observable. Finally, they can handle complex probability distributions, which is important for accurate inference in domains with many interdependent variables.
Despite these advantages, Bayesian networks also have some disadvantages. One challenge is that they can be difficult to learn because of the large number of probabilities that need to be estimated. Another challenge is that they can be computationally intensive due to the need to perform probabilistic reasoning. Finally, they can be difficult to interpret because of the way they represent uncertainty.
The above is the detailed content of Explore the concepts of Bayesian methods and Bayesian networks in depth. For more information, please follow other related articles on the PHP Chinese website!
 7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AM
7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AMGenerative AI, exemplified by chatbots like ChatGPT, offers project managers powerful tools to streamline workflows and ensure projects stay on schedule and within budget. However, effective use hinges on crafting the right prompts. Precise, detail
 Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AM
Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AMThe challenge of defining Artificial General Intelligence (AGI) is significant. Claims of AGI progress often lack a clear benchmark, with definitions tailored to fit pre-determined research directions. This article explores a novel approach to defin
 IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AM
IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AMIBM Watsonx.data: Streamlining the Enterprise AI Data Stack IBM positions watsonx.data as a pivotal platform for enterprises aiming to accelerate the delivery of precise and scalable generative AI solutions. This is achieved by simplifying the compl
 The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AM
The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AMThe rapid advancements in robotics, fueled by breakthroughs in AI and materials science, are poised to usher in a new era of humanoid robots. For years, industrial automation has been the primary focus, but the capabilities of robots are rapidly exp
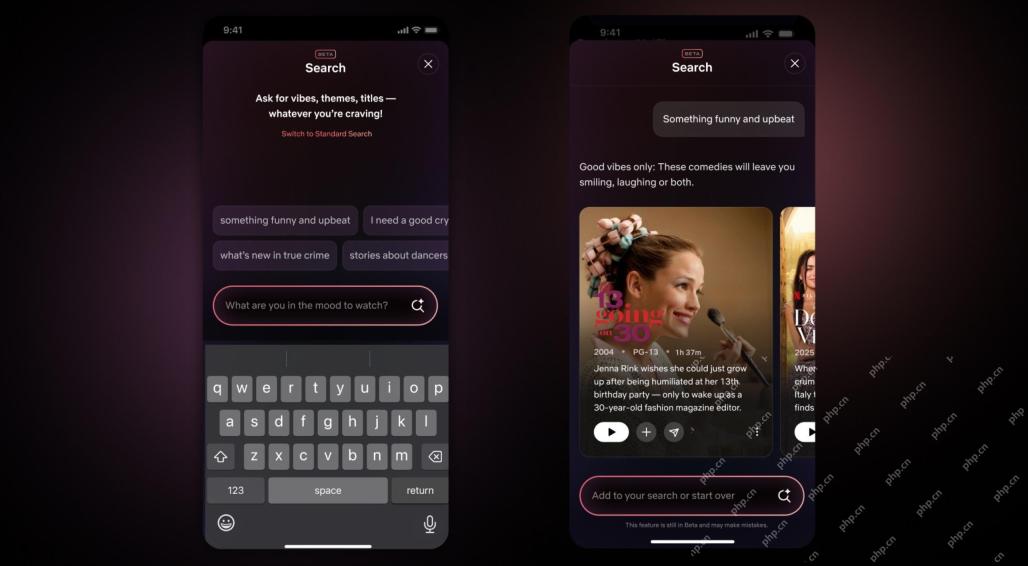 Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AM
Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AMThe biggest update of Netflix interface in a decade: smarter, more personalized, embracing diverse content Netflix announced its largest revamp of its user interface in a decade, not only a new look, but also adds more information about each show, and introduces smarter AI search tools that can understand vague concepts such as "ambient" and more flexible structures to better demonstrate the company's interest in emerging video games, live events, sports events and other new types of content. To keep up with the trend, the new vertical video component on mobile will make it easier for fans to scroll through trailers and clips, watch the full show or share content with others. This reminds you of the infinite scrolling and very successful short video website Ti
 Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AM
Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AMThe growing discussion of general intelligence (AGI) in artificial intelligence has prompted many to think about what happens when artificial intelligence surpasses human intelligence. Whether this moment is close or far away depends on who you ask, but I don’t think it’s the most important milestone we should focus on. Which earlier AI milestones will affect everyone? What milestones have been achieved? Here are three things I think have happened. Artificial intelligence surpasses human weaknesses In the 2022 movie "Social Dilemma", Tristan Harris of the Center for Humane Technology pointed out that artificial intelligence has surpassed human weaknesses. What does this mean? This means that artificial intelligence has been able to use humans
 Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AM
Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AMTransUnion's CTO, Ranganath Achanta, spearheaded a significant technological transformation since joining the company following its Neustar acquisition in late 2021. His leadership of over 7,000 associates across various departments has focused on u
 When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AM
When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AMBuilding trust is paramount for successful AI adoption in business. This is especially true given the human element within business processes. Employees, like anyone else, harbor concerns about AI and its implementation. Deloitte researchers are sc


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

SublimeText3 English version
Recommended: Win version, supports code prompts!

SublimeText3 Linux new version
SublimeText3 Linux latest version

Dreamweaver CS6
Visual web development tools







