Application of Diffusion Model in Analytical Image Processing

In the field of machine learning, diffusion models play a wide role in image processing. It is used in multiple image processing tasks, including image denoising, image enhancement, and image segmentation. The main advantage of the diffusion model is that it can effectively handle noise in images, while also enhancing image details and contrast, and enabling accurate image segmentation. In addition, diffusion models are highly computationally efficient and easy to implement. In summary, diffusion models play an important role in image processing, providing us with a powerful tool to improve image quality and extract image features.
The role of diffusion model in image processing
The diffusion model is a machine learning model based on partial differential equations, mainly used in images processing areas. Its basic principle is to simulate the physical diffusion process and achieve image denoising, enhancement, segmentation and other processing operations by controlling the parameters of partial differential equations. This model was first proposed by Perona and Malik in 1990. Its core idea is to gradually smooth or diffuse the information in the image by adjusting the parameters of the partial differential equation. Specifically, the diffusion model compares the difference between a pixel in the image and its neighbor pixels and adjusts the intensity value of the pixel based on the size of the difference. Doing so reduces noise in the image and enhances image detail. Diffusion models are widely used in image processing. For example, in terms of image denoising, it can effectively remove noise in images and make them clearer. In terms of image enhancement, it can enhance the contrast and details of the image, making the image more vivid. In image segmentation
Specifically, the role of the diffusion model in image processing is as follows:
1. Image denoising
The diffusion model can simulate the diffusion process of noise and gradually smooth the noise to achieve image denoising. Specifically, the diffusion model can use partial differential equations to describe the diffusion process of noise in the image, and smooth the noise by repeatedly iteratively solving the differential equations. This method can effectively remove common image noise such as Gaussian noise and salt-and-pepper noise.
2. Image enhancement
The diffusion model can achieve image enhancement by increasing the details and contrast of the image. Specifically, the diffusion model can use partial differential equations to describe the diffusion process of color or intensity in an image, and increase the detail and contrast of the image by controlling parameters such as diffusion coefficient and time step. This method can effectively enhance the texture, edges and other details of the image, making the image clearer and more vivid.
3. Image segmentation
The diffusion model can achieve image segmentation by simulating the diffusion process of edges. Specifically, the diffusion model can use partial differential equations to describe the diffusion process of gray values in the image, and achieve image segmentation by controlling parameters such as diffusion coefficient and time step. This method can effectively segment different objects or areas in the image, providing a basis for subsequent image analysis and processing.
Why the diffusion model can generate details when generating images
The diffusion model uses partial differential equations to describe the distribution of color or intensity in space and time. Evolution, by repeatedly iteratively solving the differential equation, the final state of the image is obtained. The reasons why the diffusion model can generate details are as follows:
1. Simulate the physical process
The basic principle of the diffusion model is to simulate the physical process , that is, the diffusion of color or intensity. In this process, the value of each pixel is affected by the pixels around it, so each pixel is updated multiple times when the differential equation is iteratively solved. This iterative process repeatedly strengthens the interaction between pixels, resulting in more detailed images.
2. Control parameters
There are many control parameters in the diffusion model, such as diffusion coefficient, time step, etc. These parameters can affect the image generation process. By adjusting these parameters, you can control the direction and level of detail in the image. For example, increasing the diffusion coefficient can cause colors or intensities to diffuse faster, resulting in a blurrier image; decreasing the time step can increase the number of iterations, resulting in a more detailed image.
3. Randomness
There are also some random factors in the diffusion model, such as initial values, noise, etc., which can increase Image variation and detail. For example, adding some noise to the initial value can make the image generation process more random, thereby generating a more detailed image; during the iterative process, you can also add some random perturbations to increase the changes and details of the image.
4. Multi-scale processing
The diffusion model can increase the details of the image through multi-scale processing. Specifically, the original image can be downsampled first to generate a smaller image, and then the diffusion model can be solved on this smaller image. The advantage of this is that it can make the details of the image more prominent and also improve the computational efficiency of the model.
5. Combine with other models
Diffusion models can be used in conjunction with other models to further increase image detail. For example, the diffusion model can be used in combination with a generative adversarial network (GAN), using the image generated by the GAN as the initial image of the diffusion model, and then further adding details through the diffusion model to generate a more realistic image.
The mathematical basis of the diffusion model
The mathematical basis of the diffusion model is the partial differential equation, its basic form is:
∂u/∂t=div(c(∇u)), where u(x,y,t) represents the image gray value at the position (x,y) at time t, c( ∇u) represents the diffusion coefficient, div represents the divergence operator, and ∇ represents the gradient operator.
This equation describes the diffusion process of gray value in a grayscale image, where c(∇u) controls the direction and speed of diffusion. Usually, c(∇u) is a nonlinear function, which can be adjusted according to the characteristics of the image to achieve different image processing effects. For example, when c(∇u) is a Gaussian function, the diffusion model can be used to remove Gaussian noise; when c(∇u) is a gradient function, the diffusion model can be used to enhance the edge features of the image.
The solution process of the diffusion model usually adopts an iterative method, that is, in each step, the gray value of the image is updated by solving the partial differential equation. For 2D images, the diffusion model can be iterated in both x and y directions. During the iteration process, parameters such as diffusion coefficient and time step can also be adjusted to achieve different image processing effects.
The reason why the loss of the diffusion model decreases very quickly
In the diffusion model, the loss function often decreases very quickly. This is due to Due to the characteristics of the diffusion model itself.
In machine learning, the application of the diffusion model is mainly to perform denoising or edge detection on images. These treatments can usually be transformed into an optimization problem of solving a partial differential equation, that is, minimizing a loss function.
In diffusion models, the loss function is usually defined as the difference between the original image and the processed image. Therefore, the process of optimizing the loss function is to adjust the model parameters to make the processed image as close as possible to the original image. Since the mathematical expression of the diffusion model is relatively simple and its model parameters are usually small, the loss function tends to decrease very quickly during the training process.
In addition, the loss function of the diffusion model is usually a convex function, which means that during the training process, the decline speed of the loss function will not have obvious oscillations, but will appear smooth. downward trend. This is also one of the reasons why the loss function decreases quickly.
In addition to the above reasons, the rapid decline of the loss function of the diffusion model is also related to its model structure and optimization algorithm. Diffusion models usually use implicit numerical methods to solve partial differential equations. This method has high computational efficiency and numerical stability, and can effectively solve numerical errors and time-consuming problems in the numerical solution process. In addition, the optimization algorithm of the diffusion model usually uses optimization algorithms such as gradient descent. These algorithms can effectively reduce the computational complexity when processing high-dimensional data, thereby speeding up the decline of the loss function.
The rapid decline of the loss function of the diffusion model is also related to the nature of the model and parameter selection. In diffusion models, the parameters of the model are usually set as constants or time-related functions. The choice of these parameters can affect the performance of the model and the rate of decline of the loss function. Generally speaking, setting appropriate parameters can speed up model training and improve model performance.
In addition, in the diffusion model, there are some optimization techniques that can further speed up the decline of the loss function. For example, an optimization algorithm using adaptive step size can automatically adjust the update step size of model parameters according to changes in the loss function, thereby speeding up the convergence of the model. In addition, using techniques such as batch normalization and residual connection can also effectively improve the training speed and performance of the model.
Diffusion model and neural network
In machine learning, diffusion model is mainly used in the fields of image processing and computer vision. For example, the diffusion model can be used to perform image denoising or edge detection. In addition, the diffusion model can also be used in image segmentation, target recognition and other fields. The advantage of the diffusion model is that it can handle high-dimensional data and has strong noise immunity and smoothness, but its computational efficiency is low and it requires a lot of computing resources and time.
Neural networks are widely used in machine learning and can be used in image recognition, natural language processing, speech recognition and other fields. Compared with diffusion models, neural networks have stronger expression and generalization capabilities, can handle various types of data, and can automatically learn features. However, the neural network has a large number of parameters and requires a large amount of data and computing resources for training. At the same time, its model structure is relatively complex and requires certain technology and experience to design and optimize.
In practical applications, diffusion models and neural networks are often used in combination to give full play to their respective advantages. For example, in image processing, you can first use the diffusion model to denoise and smooth the image, and then input the processed image into the neural network for feature extraction and classification recognition. This combination can improve the accuracy and robustness of the model, while also accelerating the model training and inference process.
The above is the detailed content of Application of Diffusion Model in Analytical Image Processing. For more information, please follow other related articles on the PHP Chinese website!
 7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AM
7 Powerful AI Prompts Every Project Manager Needs To Master NowMay 08, 2025 am 11:39 AMGenerative AI, exemplified by chatbots like ChatGPT, offers project managers powerful tools to streamline workflows and ensure projects stay on schedule and within budget. However, effective use hinges on crafting the right prompts. Precise, detail
 Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AM
Defining The Ill-Defined Meaning Of Elusive AGI Via The Helpful Assistance Of AI ItselfMay 08, 2025 am 11:37 AMThe challenge of defining Artificial General Intelligence (AGI) is significant. Claims of AGI progress often lack a clear benchmark, with definitions tailored to fit pre-determined research directions. This article explores a novel approach to defin
 IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AM
IBM Think 2025 Showcases Watsonx.data's Role In Generative AIMay 08, 2025 am 11:32 AMIBM Watsonx.data: Streamlining the Enterprise AI Data Stack IBM positions watsonx.data as a pivotal platform for enterprises aiming to accelerate the delivery of precise and scalable generative AI solutions. This is achieved by simplifying the compl
 The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AM
The Rise of the Humanoid Robotic Machines Is Nearing.May 08, 2025 am 11:29 AMThe rapid advancements in robotics, fueled by breakthroughs in AI and materials science, are poised to usher in a new era of humanoid robots. For years, industrial automation has been the primary focus, but the capabilities of robots are rapidly exp
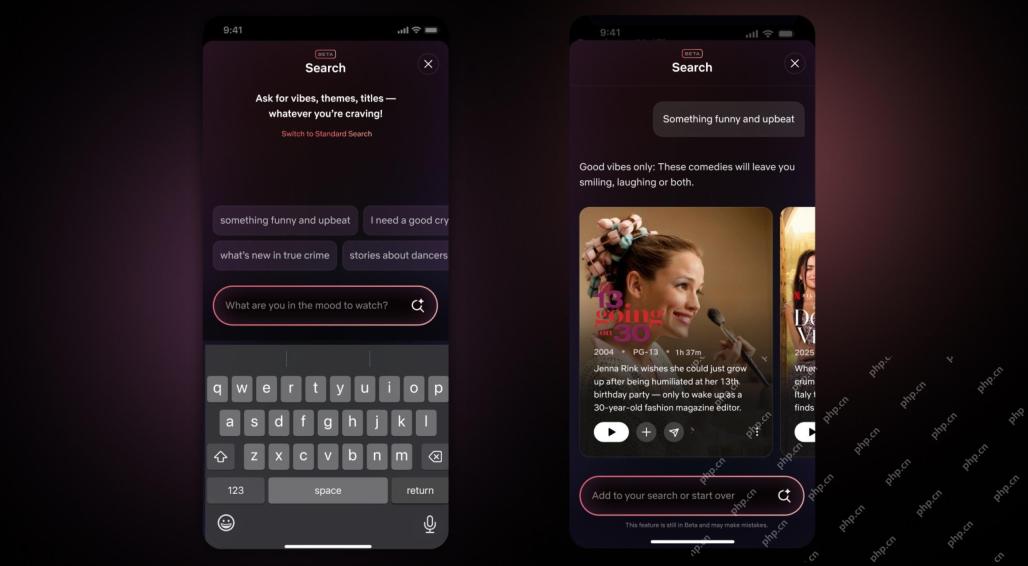 Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AM
Netflix Revamps Interface — Debuting AI Search Tools And TikTok-Like DesignMay 08, 2025 am 11:25 AMThe biggest update of Netflix interface in a decade: smarter, more personalized, embracing diverse content Netflix announced its largest revamp of its user interface in a decade, not only a new look, but also adds more information about each show, and introduces smarter AI search tools that can understand vague concepts such as "ambient" and more flexible structures to better demonstrate the company's interest in emerging video games, live events, sports events and other new types of content. To keep up with the trend, the new vertical video component on mobile will make it easier for fans to scroll through trailers and clips, watch the full show or share content with others. This reminds you of the infinite scrolling and very successful short video website Ti
 Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AM
Long Before AGI: Three AI Milestones That Will Challenge YouMay 08, 2025 am 11:24 AMThe growing discussion of general intelligence (AGI) in artificial intelligence has prompted many to think about what happens when artificial intelligence surpasses human intelligence. Whether this moment is close or far away depends on who you ask, but I don’t think it’s the most important milestone we should focus on. Which earlier AI milestones will affect everyone? What milestones have been achieved? Here are three things I think have happened. Artificial intelligence surpasses human weaknesses In the 2022 movie "Social Dilemma", Tristan Harris of the Center for Humane Technology pointed out that artificial intelligence has surpassed human weaknesses. What does this mean? This means that artificial intelligence has been able to use humans
 Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AM
Venkat Achanta On TransUnion's Platform Transformation And AI AmbitionMay 08, 2025 am 11:23 AMTransUnion's CTO, Ranganath Achanta, spearheaded a significant technological transformation since joining the company following its Neustar acquisition in late 2021. His leadership of over 7,000 associates across various departments has focused on u
 When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AM
When Trust In AI Leaps Up, Productivity FollowsMay 08, 2025 am 11:11 AMBuilding trust is paramount for successful AI adoption in business. This is especially true given the human element within business processes. Employees, like anyone else, harbor concerns about AI and its implementation. Deloitte researchers are sc


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

Dreamweaver Mac version
Visual web development tools

WebStorm Mac version
Useful JavaScript development tools







