Home >Technology peripherals >AI >With nearly half the parameters, the performance is close to Google Minerva, another large mathematical model is open source
With nearly half the parameters, the performance is close to Google Minerva, another large mathematical model is open source
- PHPzforward
- 2023-10-21 14:13:011350browse
Nowadays, language models trained on various text mixed data will show very general language understanding and generation capabilities and can be used as basic models to adapt to various applications. Applications such as open dialogue or instruction tracking require balanced performance across the entire natural text distribution and therefore prefer general-purpose models.
However, if one wants to maximize performance within a certain domain (such as medicine, finance, or science), then domain-specific language models may be available at a given computational cost Superior capabilities, or providing a given level of capabilities at a lower computational cost.
Researchers from Princeton University, EleutherAI and others have trained a domain-specific language model to solve mathematical problems. They believe that: first, solving mathematical problems requires pattern matching with a large amount of professional prior knowledge, so it is an ideal environment for domain adaptability training; second, mathematical reasoning itself is the core task of AI; finally, the ability to perform strong mathematical reasoning Language models are the upstream of many research topics, such as reward modeling, inference reinforcement learning, and algorithmic reasoning.
Therefore, they propose a method to adapt language models to mathematics through continuous pre-training of Proof-Pile-2. Proof-Pile-2 is a mix of mathematics-related text and code. Applying this approach to Code Llama results in LLEMMA: a base language model for 7B and 34B, with greatly improved mathematical capabilities.

##Paper address: https://arxiv.org/pdf/2310.10631.pdf
Project address: https://github.com/EleutherAI/math-lm
LLEMMA 7B’s 4-shot Math performance far exceeds Google Minerva 8B, and LLEMMA 34B is The performance is close to Minerva 62B with nearly half the parameters.

Specifically, the contributions of this article are as follows:
- 1. Trained and published LLEMMA model: 7B and 34B language models dedicated to mathematics. The LLEMMA model is the state of the art in base models publicly released on MATH.
- 2. Released AlgebraicStack, a dataset containing 11B code tokens specifically related to mathematics.
- 3. It is demonstrated that LLEMMA is capable of solving mathematical problems using computational tools, namely the Python interpreter and the formal theorem prover.
- 4. Unlike previous mathematical language models (such as Minerva), the LLEMMA model is open-ended. The researchers made the training data and code available to the public. This makes LLEMMA a platform for future research in mathematical reasoning.
Method Overview
LLEMMA is a 70B and 34B language model specifically for mathematics. It is obtained by continuing to pre-train the code Llama on Proof-Pile-2.

The researchers created Proof-Pile-2, a 55B token mixture of scientific papers, network data containing mathematics, and mathematical code. The knowledge deadline for Proof-Pile-2 is April 2023, except for the Lean proofsteps subset.

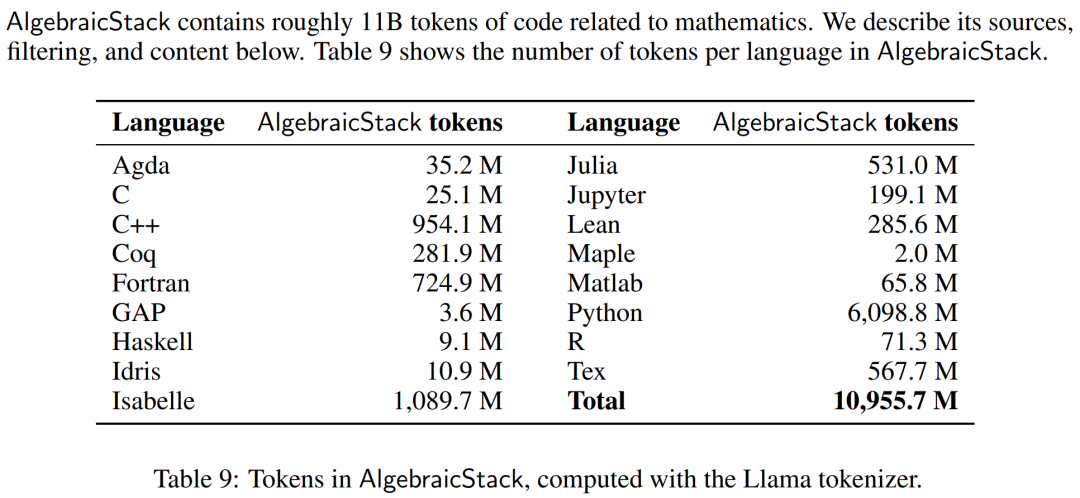
The researchers used OpenWebMath, a 15B token dataset composed of high-quality web pages, filtered for mathematical content. OpenWebMath filters CommonCrawl web pages based on math-related keywords and classifier-based math scores, preserves math formatting (e.g., LATEX, AsciiMath), and includes additional quality filters (e.g., plexity, domain, length) and near-duplication. In addition to this, the researchers also used the ArXiv subset of RedPajama, which is an open rendition of the LLaMA training dataset. The ArXiv subset contains 29B chunks. The training mixture consists of a small amount of general domain data and acts as a regularizer. Since the pre-training dataset for LLaMA 2 is not yet publicly available, the researchers used Pile as an alternative training dataset. Models and training Each model is initialized from Code Llama, which in turn is initialized from Llama 2, using a deconder only transformer structure, is trained on 500B code tokens. The researchers continued to train the Code Llama model on Proof-Pile-2 using the standard autoregressive language modeling objective. Here, the LLEMMA 7B model has 200B tokens and the LLEMMA 34B model has 50B tokens. The researchers used the GPT-NeoX library to train the above two models with bfloat16 mixed precision on 256 A100 40GB GPUs. They used tensor parallelism with world size 2 for LLEMMA-7B and tensor parallelism with world size 8 for 34B, as well as ZeRO Stage 1 shard optimizer states across data-parallel replicas. Flash Attention 2 is also used to increase throughput and further reduce memory requirements. LLEMMA 7B has been trained for 42,000 steps, with a global batch size of 4 million tokens and a context length of 4096 tokens. This is equivalent to 23,000 A100 hours. The learning rate warms up to 1·10^−4 after 500 steps and then cosineally decays to 1/30 of the maximum learning rate after 48,000 steps. LLEMMA 34B has been trained for 12,000 steps. The global batch size is also 4 million tokens and the context length is 4096. This is equivalent to 47,000 A100 hours. The learning rate warms up to 5·10^−5 after 500 steps, and then decays to 1/30 of the peak learning rate. In the experimental part, the researcher aimed to evaluate whether LLEMMA can be used as a basic model for mathematical texts. They utilize few-shot evaluation to compare LLEMMA models and focus primarily on SOTA models that are not fine-tuned on supervised samples of mathematical tasks. The researchers first used chain-of-thinking reasoning and majority voting methods to evaluate LLEMMA’s ability to solve mathematical problems. The evaluation benchmarks included MATH and GSM8k. Then explore the use of few-shot tools and theorem proving. Finally, the impact of memory and data mixing is studied. Solve math problems using Chains of Thoughts (CoT) These tasks include problems expressed as LATEX or natural language Generate independent text answers without using external tools. The evaluation benchmarks used by researchers include MATH, GSM8k, OCWCourses, SAT and MMLU-STEM. The results are shown in Table 1 below. LLEMMA’s continuous pre-training on the Proof-Pile-2 corpus improved the few-sample performance on 5 mathematical benchmarks, among which LLEMMA 34B improved on GSM8k It is 20 percentage points higher than Code Llama on MATH and 13 percentage points higher than Code Llama on MATH. At the same time LLEMMA 7B outperformed the proprietary Minerva model. Therefore, the researchers concluded that continuous pre-training on Proof-Pile-2 can help improve the ability of the pre-trained model to solve mathematical problems. Use tools to solve math problems These tasks include using computational tools to solve problems. The evaluation benchmarks used by researchers include MATH Python and GSM8k Python. The results are shown in Table 3 below, LLEMMA outperforms Code Llama on both tasks. The performance on MATH and GSM8k using both tools is also better than without the tools. Formal Mathematics Proof-Pile-2’s AlgebraicStack dataset holds 1.5 billion tokens of formal mathematical data, including formal proofs extracted from Lean and Isabelle. While a full study of formal mathematics is beyond the scope of this article, we evaluate the few-shot performance of LLEMMA on the following two tasks. Informal to formal proof task, that is, given a formal proposition, an informal LATEX proposition, and an informal LATEX proof In this case, generate a formal proof; Form-to-form proof task is to prove a formal proposition by generating a series of proof steps (or strategies). The results are shown in Table 4 below. LLEMMA’s continuous pre-training on Proof-Pile-2 improved the few-sample performance on two formal theorem proving tasks. The impact of data mixing When training a language model, a common approach is to train based on the mixing weights High-quality subsets of the data are upsampled. The researchers selected the blend weights by performing short training on several carefully selected blend weights. We then selected hybrid weights that minimized perplexity on a set of high-quality held-out texts (here we used the MATH training set). Table 5 below shows the MATH training set perplexity of the model after training with different data mixes such as arXiv, web and code. For more technical details and evaluation results, please refer to the original paper. Evaluation results




The above is the detailed content of With nearly half the parameters, the performance is close to Google Minerva, another large mathematical model is open source. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- What does the python ipo model refer to?
- What type of data model does sql server belong to?
- What is the main contribution of the Turing machine computational model?
- Just train once to generate new 3D scenes! The evolution history of Google's 'Light Field Neural Rendering”
- Used for lidar point cloud self-supervised pre-training SOTA!

