Think, think, think without stopping, Thinking Tree ToT "Military Training" LLM

Large language models such as GPT and PaLM are becoming increasingly adept at handling tasks such as mathematical, symbolic, common sense, and knowledge reasoning. Perhaps surprisingly, the basis for all these advances remains the original autoregressive mechanism for generating text. It makes decisions token by token and generates text in a left-to-right fashion. Is such a simple mechanism sufficient to build a language model for a general problem solver? If not, what issues will challenge the current paradigm, and what alternative mechanisms should be employed?

The literature on human cognition provides some clues to answer these questions. Research on the "dual process" model shows that people have two modes when making decisions: one is a fast, automatic, and unconscious mode (System 1), and the other is a slow, deliberate, and conscious mode. (System 2). These two patterns have previously been associated with various mathematical models used in machine learning. For example, research on reinforcement learning in humans and other animals explores whether they engage in associative “model-free” learning or more deliberate “model-based” planning. The simple associative token-level selection of language models is also similar to "System 1" and thus may benefit from the enhancement of a more thoughtful "System 2" planning process that maintains and explores multiple alternatives to the current selection, not just choose one. Additionally, it evaluates its current state and actively looks ahead or back to make more global decisions.

In order to design such a planning process, researchers from Princeton University and Google DeepMind chose to first review the origins of artificial intelligence (and cognitive science) and draw on the work of Newell, Shaw and Simon. Inspiration for the planning process explored in the 1950s. Newell and colleagues describe problem solving as a search of a combinatorial problem space represented as a tree. Therefore, they proposed a Tree of Thought (ToT) framework adapted to language models for general problem solving.

Paper link: https://arxiv.org/pdf/2305.10601 .pdf

Project address: https://github.com/ysymyth/tree-of-thought-llm

As shown in Figure 1, existing methods solve the problem by sampling continuous language sequences, while ToT actively maintains a thought tree, where each thought is a coherent language sequence, as Intermediate steps in problem solving (Table 1).

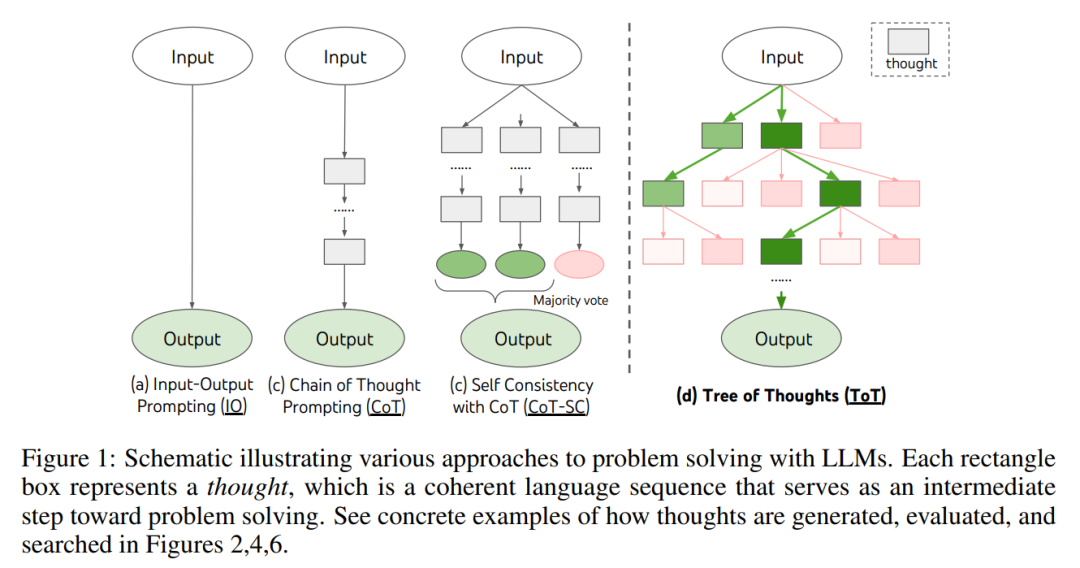
## Such a The advanced semantic unit enables LM to self-evaluate the contribution of different intermediate thoughts to the progress of problem solving through a thoughtful reasoning process (Figures 2, 4, 6). Implementing search heuristics through LM self-evaluation and deliberation is a novel approach, as previous search heuristics were either programmed or learned.

#Finally, the researchers based this The language's ability to generate and evaluate diverse thoughts is combined with search algorithms, such as Breadth-First Search (BFS) or Depth-First Search (DFS), which allow systematic exploration of thought trees, with look-ahead and backtracking capabilities.

In the experimental phase, the researchers set up three tasks, namely 24-point game, creative writing and crossword puzzle (Table 1). These problems are quite challenging for the existing LM inference method, even if GPT-4 is no exception. These tasks require deductive, mathematical, general knowledge, lexical reasoning skills, and a way to incorporate systematic planning or search. Experimental results show that ToT achieves superior results on these three tasks because it is versatile and flexible enough to support different levels of thinking, different ways of generating and evaluating thinking, and adapts to different natures of problems. Search algorithm. Through systematic experimental ablation analysis, the authors also explore how these choices affect model performance and discuss future directions for training and using LMs.

Thinking Trees: Leveraging Language Models for Thoughtful Problem Solving

A true problem solving process involves iteratively using available information to initiate exploration, which in turn reveals more information, until a final discovery is made Ways to implement solutions. ——Newell et al

Research on human problem solving shows that humans solve problems by searching a combinatorial problem space. This can be viewed as a tree, where nodes represent partial solutions and branches correspond to operators that modify them. Which branch is chosen is determined by heuristics that help navigate the problem space and guide the problem solver in the direction of the solution. This perspective highlights two key shortcomings of existing approaches that use language models to solve general problems: 1) Locally, they do not explore different continuations in the thought process – branches of the tree. 2) Globally, they do not include any kind of planning, looking ahead, or backtracking to help evaluate these different options—the kind of heuristic-guided search that seems to be characteristic of human problem solving.

In order to solve these problems, the author introduces the tree of thinking (ToT), which is a paradigm that allows language models to explore multiple reasoning methods on the thinking path (Figure 1 (c )). ToT frames any problem as a search of a tree, where each node is a state s = [x, z_1・・・i ], representing a partial solution with input and a sequence of thoughts so far. Specific examples of ToT include answering the following four questions:

• #1. How to break down the intermediate process into thinking steps;
• 2 . How to generate potential thoughts from each state;
• 3. How to evaluate states heuristically;
• 4. What search algorithm to use.

1. Thinking decomposition. While CoT samples thinking coherently without explicit decomposition, ToT exploits problem properties to design and decompose intermediate thinking steps. As shown in Table 1, depending on the problem, the thought can be a few words (crossword puzzle), an equation (24-dot game), or a writing plan (creative writing). Generally speaking, the thinking should be "small" enough so that LM can generate the expected diversity of samples (such as generating a book that is too "big" to be coherent), but the thinking should be "big" enough. So that the LM can evaluate its prospects for solving the problem (for example, generating a token is usually too small to evaluate).

2. Thought generator G (p_θ, s, k). Given a tree state s = [x, z_1・・・i], this study utilizes two strategies to generate k candidates for the next thinking step.

3. State evaluator V (p_θ, S). Given the boundaries of different states, the state evaluator evaluates their progress toward solving the problem to determine which states should continue to be explored, and in what order. While heuristics are a standard way to solve search problems, they are often either programmatic (e.g. DeepBlue) or learned (e.g. AlphaGo). This article proposes a third alternative, by using language to intentionally reason about states. Where applicable, such thoughtful heuristics can be more flexible than programming rules and more efficient than learning models.

Similar to the Thought Generator, consider two strategies to evaluate states individually or together:

• (1) Evaluate each state independently state
• (2) Cross-state voting

These two strategies can prompt LM multiple times to integrate value or vote As a result, time, resources, and costs are exchanged for more reliable and robust heuristics.

4. Search algorithm. Finally, within the ToT framework it is possible to plug and play different search algorithms based on the tree structure. This article explores two relatively simple search algorithms and leaves more advanced algorithms for future research:

• (1) Breadth-First Search (BFS) (Algorithm 1 )
• (2) Depth First Search (DFS) (Algorithm 2)

Conceptually, ToT serves as a language model Methods for solving general problems have several advantages:

• (1) Universality. IO, CoT, CoT-sc and self-refinement can be seen as special cases of ToT (i.e. trees with limited depth and breadth; Figure 1);
• (2) Modularization. Basic LM as well as thought decomposition, generation, evaluation and search processes can all vary independently;
• (3) Adaptability. Can adapt to different problem attributes, LM capabilities and resource constraints;
• (4) Convenience. No additional training is required, just a pre-trained LM is sufficient.

Experimental results

The study proposed three tasks, even using the most advanced language model GPT-4, through standard IO prompting or thought chain (CoT) prompting for sampling, these tasks remain challenging.

24 Dot Math Game

Given four numbers, players need to use these four numbers within a limited time numbers and basic math symbols (plus, minus, multiplication, division) to create an expression that evaluates to 24. For example, given the numbers: 4, 6, 8, 2, a possible solution is: (8 ÷ (4 - 2)) × 6 = 24.

As shown in Table 2, using IO, CoT, and CoT-SC prompting methods performed poorly on the task, achieving only 7.3%, 4.0%, and 9.0% success rates. In comparison, ToT with b(breadth) = 1 has achieved a success rate of 45%, and with b = 5 it reaches 74%. They also considered the oracle setting of IO/CoT to calculate the success rate by using the best value among k samples (1 ≤ k ≤ 100).

To compare IO/CoT (k best results) with ToT, researchers consider counting the number of tree nodes visited in each task in ToT, where b = 1・・・5, and map the 5 success rates in Figure 3 (a), treating IO/CoT (k best results) as visiting k nodes in a gambling machine. Unsurprisingly, CoT is more scalable than IO, and the best 100 CoT samples achieved a success rate of 49%, which is still far less than exploring more nodes in ToT (b > 1).

Figure 3 (b) below breaks down the performance of CoT and ToT samples when the task fails. Condition. It is worth noting that about 60% of CoT samples already failed after the first step of generating, equivalent to generating the first three words (e.g. “4 9”). This makes the problem of decoding directly from left to right even more obvious.

##Creative Writing

The researchers also invented a creative writing task, inputting 4 random sentences and outputting a coherent article containing four paragraphs, each ending with 4 input sentences. Such tasks are open-ended and exploratory, challenging creative thinking and high-level planning.

Figure 5 (a) below shows the average score of GPT-4 across 100 tasks, where ToT (7.56) generates more results than IO (6.19) and CoT (6.93) Coherent paragraphs. Although such automatic measures can be noisy, Figure 5(b) confirms that humans prefer ToT to CoT in 41 out of 100 passage pairs, while only 21 pairs prefer CoT to ToT (the other 38 pairs were found "similarly coherent").

Finally, the iterative optimization algorithm achieved better results on this natural language task, with the IO consistency score increasing from 6.19 to 7.67 and the ToT consistency score increasing from 7.56 to 7.91. The researchers believe that this can be seen as the third method of thinking generation in the ToT framework. New thinking can be generated from the refinement of old thinking rather than sequential generation.

##Mini crossword puzzle

In "24-Point Math Game" and creative writing, ToT is relatively simple - it takes up to 3 thinking steps to achieve the final output. Researchers will explore the 5×5 mini-crossword puzzle as a more difficult layer of search questions about natural language. Again, the goal this time is not just solving the task, as general crossword puzzles can be easily solved by a specialized NLP pipeline that leverages large-scale retrieval instead of LM. Instead, researchers aim to explore the limits of a language model as a general problem solver, explore its own thinking, and use rigorous reasoning as a heuristic to guide its exploration.

As shown in Table 3 below, the IO and CoT prompting methods performed poorly, with word-level success rates below 16%, while ToT significantly improved all metrics, achieving 60% Word level success rate, 4 games solved out of 20. This improvement is not surprising considering that IO and CoT lack mechanisms to try different cues, change decisions, or backtrack.

The above is the detailed content of Think, think, think without stopping, Thinking Tree ToT "Military Training" LLM. For more information, please follow other related articles on the PHP Chinese website!