How to implement decision tree classification algorithm in python

Pre-information

1. Decision tree

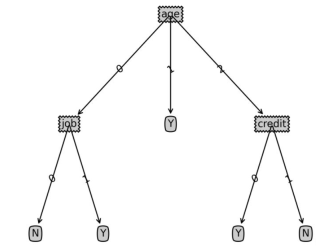
The rewritten sentence: In supervised learning, a commonly used classification algorithm is decision tree, which is based on a batch of samples, each sample contains a set of attributes and corresponding classification results. Using these samples for learning, the algorithm can generate a decision tree that can correctly classify new data

2. Sample data

Assume that there are 14 existing users, and their personal attributes The data on whether to purchase a certain product is as follows:

##No.AgeIncome rangeType of workCredit RatingPurchasing Decision01High UnstablePoorNo02高UnstableGoodNo0330-40HighUnstablePooris04>40MediumUnstablePoorYes##050607080910##11MediumStableGoodYes30-4030-40>40##

Ce tree classification algorithm

1. Construct a data set

In order to facilitate processing, the simulation data is converted into numerical list data according to the following rules:

Age: < ;30 is assigned a value of 0; 30-40 is assigned a value of 1; >40 is assigned a value of 2

Income: low is 0; medium is 1; high is 2

Work nature: unstable 0; stable is 1

Credit rating: poor is 0; good is 1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,'N'],
            [0,2,0,1,'N'],
            [1,2,0,0,'Y'],
            [2,1,0,0,'Y'],
            [2,0,1,0,'Y'],
            [2,0,1,1,'N'],
            [1,0,1,1,'Y'],
            [0,1,0,0,'N'],
            [0,0,1,0,'Y'],
            [2,1,1,0,'Y'],
            [0,1,1,1,'Y'],
            [1,1,0,1,'Y'],
            [1,2,1,0,'Y'],
            [2,1,0,1,'N'],]
    labels=['age','income','job','credit']
    return dataSet,labels

Call the function to get data:

ds1,lab = createdataset()
print(ds1)
print(lab)

[[0, 2 , 0, 0, ‘N’], [0, 2, 0, 1, ‘N’], [1, 2, 0, 0, ‘Y’], [2, 1, 0, 0, ‘Y’], [2, 0, 1, 0, ‘Y’], [2, 0, 1, 1, ‘N’], [1, 0, 1, 1, ‘Y’] , [0, 1, 0, 0, ‘N’], [0, 0, 1, 0, ‘Y’], [2, 1, 1, 0, ‘Y’], [0, 1 , 1, 1, ‘Y’], [1, 1, 0, 1, ‘Y’], [1, 2, 1, 0, ‘Y’], [2, 1, 0, 1, ‘N’]]
[‘age’, ‘income’, ‘job’, ‘credit’]

2. Data set information entropy

Information entropy, also known as Shannon entropy, is the expectation of random variables. Measures the degree of uncertainty of information. The greater the entropy of information, the harder it is to figure out the information. Processing information is to clarify the information, which is the process of entropy reduction.

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

Sample data information entropy:

shan = calcShannonEnt(ds1)
print(shan)

0.9402859586706309

3. Information gain

Information gain: used to measure attribute A Reduce the contribution of the sample set X entropy. The greater the information gain, the more suitable it is for classifying X.

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

The above code implements the ID3 decision tree learning algorithm based on information entropy gain. Its core logical principle is: select each attribute in the attribute set in turn, and divide the sample set into several subsets according to the value of this attribute; calculate the information entropy of these subsets, and the difference between it and the information entropy of the sample is based on The information entropy gain of this attribute segmentation; find the attribute corresponding to the largest gain among all gains, which is the attribute used to segment the sample set.

Calculate the best split sample attribute of the sample, and the result is displayed in column 0, which is the age attribute:

col = chooseBestFeatureToSplit(ds1)
col

0

4. Construction decision The tree

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

majorityCnt function is used to handle the following situation: when the final ideal decision tree should reach the bottom along the decision branch, all samples should have the same classification result. However, in real samples, it is inevitable that all attributes are consistent but the classification results are different. In this case, majorityCnt adjusts the classification labels of such samples to the classification result with the most occurrences.

createTree is the core task function. It calls the ID3 information entropy gain algorithm for all attributes in sequence to calculate and process, and finally generates a decision tree.

5. Construct a decision tree by instantiation

Use sample data to construct a decision tree:

Tree = createTree(ds1, lab)
print("样本数据决策树：")
print(Tree)

Sample data decision tree:
{‘age’: {0: {‘job’: {0: ‘N’, 1: ‘Y’}},
1: ‘Y’,
2: {‘credit’: {0: ‘Y’, 1: ‘N’}}}}

6. Test sample classification

Give a new user Information to determine whether he or she will buy a certain product:

>40	Low	Stable	Poor	Yes
> 40	Low	Stable	Good	No
30- 40	Low	Stable	Good	Yes
	Medium	Unstable	Poor	No
	Low	Stable	Poor	is
>40	Medium	Stable	Poor	Yes
				##12
Medium	Unstable	Good	Yes		13
High	Stable	Poor	is		14
Medium	Unstable	Good	No

##AgeIncome rangeNature of workCredit rating ##

def classify(inputtree,featlabels,testvec):
    firststr = list(inputtree.keys())[0]
    seconddict = inputtree[firststr]
    featindex = featlabels.index(firststr)
    for key in seconddict.keys():
        if testvec[featindex]==key:
            if type(seconddict[key]).__name__=='dict':
                classlabel=classify(seconddict[key],featlabels,testvec)
            else:
                classlabel=seconddict[key]
    return classlabel

labels=['age','income','job','credit']
tsvec=[0,0,1,1]
print('result:',classify(Tree,labels,tsvec))
tsvec1=[0,2,0,1]
print('result1:',classify(Tree,labels,tsvec1))

Low	Stable	Good		High	Unstable	Good

result: Y

result1: N

Post information: Drawing decision tree code

The following code is used to draw decision tree graphics, not the focus of the decision tree algorithm. If you are interested, you can refer to it for learning

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.savefig('决策树.png',dpi=300,bbox_inches='tight')
    plt.show()

The above is the detailed content of How to implement decision tree classification algorithm in python. For more information, please follow other related articles on the PHP Chinese website!