Understand and unify 14 attribution algorithms to make neural networks interpretable

Although DNNs have achieved widespread success in various practical applications, their processes are often viewed as black boxes because it is difficult to explain how DNNs make decisions. The lack of interpretability compromises the reliability of DNNs, thus hindering their widespread application in high-stakes tasks such as autonomous driving and AI medicine. Therefore, explainable DNNs have attracted increasing attention.

As a typical perspective for explaining DNN, the attribution method aims to calculate the attribution/importance/contribution score of each input variable to the network output. For example, given a pretrained DNN for image classification and an input image, the attribute score for each input variable refers to the numerical impact of each pixel on the classification confidence score.

Although researchers have proposed many attribution methods in recent years, most of them are based on different heuristics. There is currently a lack of a unified theoretical perspective to test the correctness of these attribution methods, or at least to mathematically elucidate their core mechanisms.

Researchers have tried to unify different attribution methods, but these studies have only covered a few methods.

In this article, we propose a "unified explanation of the intrinsic mechanisms of 14 input unit importance attribution algorithms."

Paper address: https://arxiv.org/pdf/2303.01506.pdf

In fact, whether it is "12 algorithms to improve resistance to migration" or "14 input unit importance attribution algorithms", they are all hardest hit by engineering algorithms. In these two fields, most algorithms are empirical. People design some plausible engineering algorithms based on experimental experience or intuitive understanding. Most studies have not made rigorous definitions and theoretical demonstrations of "what exactly is the importance of input units". A few studies have certain demonstrations, but they are often very imperfect. Of course, the problem of "lack of rigorous definitions and demonstrations" pervades the entire field of artificial intelligence, but is particularly prominent in these two directions.

• First, in an environment where numerous empirical attribution algorithms flood the field of interpretable machine learning, we hope to demonstrate that “all 14 attribution algorithms (interpreting neural network inputs The internal mechanism of the unit importance algorithm can be expressed as a distribution of the interaction utility modeled by the neural network, and different attribution algorithms correspond to different interaction utility distribution proportions." In this way, although different algorithms have completely different design focuses (for example, some algorithms have an outlined objective function, and some algorithms are pure pipelines), we found that mathematically, these algorithms can be included in the "interaction utility" "distribution" of narrative logic.
• Based on the above interactive utility allocation framework, we can further propose three evaluation criteria for the neural network input unit importance attribution algorithm to measure the input unit importance predicted by the attribution algorithm. Is the value reasonable?

Of course, our theoretical analysis is not only applicable to the 14 attribution algorithms, and can theoretically unify more similar research. Due to limited manpower, we only discuss 14 algorithms in this paper.

The real difficulty in research is that different empirical attribution algorithms are often built on different intuitions, and each paper only strives to "justify itself" from its own perspective. , each design attribution algorithms based on different intuitions or perspectives, but lacks a standardized mathematical language to uniformly describe the essence of various algorithms.

Algorithm Review

Before talking about mathematics, this article will briefly review the previous algorithm from an intuitive level.

1. Gradient-based attribution algorithm. This type of algorithm generally believes that the gradient of the output of the neural network to each input unit can reflect the importance of the input unit. For example, the Gradient*Input algorithm models the importance of an input unit as the element-wise product of the gradient and the input unit value. Considering that the gradient can only reflect the local importance of the input unit, the Smooth Gradients and Integrated Gradients algorithms model the importance as the element-wise product of the average gradient and the input unit value, where the average gradient in these two methods refers to the input sample neighbor respectively. The average value of the gradient within the domain or the average gradient of the linear interpolation point between the input sample and the baseline point. Similarly, the Grad-CAM algorithm takes the average of the network output over all feature gradients in each channel to calculate the importance score. Furthermore, the Expected Gradients algorithm believes that selecting a single benchmark point will often lead to biased attribution results, thereby proposing to model importance as the expectation of Integrated Gradients attribution results under different benchmark points.

#2. Attribution algorithm based on layer-by-layer backpropagation. Deep neural networks are often extremely complex, and the structure of each layer of neural network is relatively simple (for example, deep features are usually the linear addition and nonlinear activation function of shallow features), which facilitates analysis of the importance of shallow features to deep features. . Therefore, this type of algorithm obtains the importance of the input unit by estimating the importance of mid-level features and propagating these importance layer by layer until the input layer. Algorithms in this category include LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap, etc. The fundamental difference between different backpropagation algorithms is that they use different importance propagation rules layer by layer.

#3. Occlusion-based attribution algorithm. This type of algorithm infers the importance of an input unit based on the impact of occluding an input unit on the model output. For example, the Occlusion-1 (Occlusion-patch) algorithm models the importance of the i-th pixel (pixel block) as the change in output when pixel i is unoccluded and occluded when other pixels are not occluded. The Shapley value algorithm comprehensively considers all possible occlusion situations of other pixels, and models the importance as the average of the output changes corresponding to pixel i under different occlusion situations. Research has proven that Shapley value is the only attribution algorithm that satisfies the axioms of linearity, dummy, symmetry, and efficiency.

Unify the inner mechanism of 14 empirical attribution algorithms

After in-depth study of various empirical attribution algorithms, we can’t help but think about a question: at the mathematical level What problem is the attribution of neural networks solving? Is there some unified mathematical modeling and paradigm behind many empirical attribution algorithms? To this end, we try to consider the above issues starting from the definition of attribution. Attribution refers to the importance score/contribution of each input unit to the neural network output. Then, the key to solving the above problem is to (1) model the "influence mechanism of the input unit on the network output" at the mathematical level, and (2) explain how many empirical attribution algorithms use this influence mechanism to design importance Attribution formula.

Regarding the first key point, our research found that each input unit often affects the output of the neural network in two ways. On the one hand, a certain input unit does not need to rely on other input units and can act independently and affect the network output. This type of influence is called "independent effect". On the other hand, an input unit needs to cooperate with other input units to form a certain pattern, thereby affecting the network output. This type of influence is called "interaction effect". Our theory proves that the output of the neural network can be rigorously deconstructed into the independent effects of different input variables, as well as the interactive effects between input variables in different sets.

Among them, represents the independent effect of the i-th input unit, represents the multiple effects in the set S The interaction effect between input units. Regarding the second key point, we discovered that the internal mechanisms of all 14 existing empirical attribution algorithms can represent a distribution of the above independent utility and interactive utility, and different attribution The algorithm distributes the independent utility and interactive utility of the neural network input units in different proportions. Specifically, let ​ ​ represents the attribution score of the i-th input unit. We rigorously prove that the obtained by all 14 empirical attribution algorithms can be uniformly expressed as the following mathematical paradigm (i.e., the weighted sum of independent utility and interactive utility): ​#​

Among them, reflects the proportion of the independent effect of the j-th input unit assigned to the i-th input unit, represents the proportion of the interaction effect between multiple input units in the set S that is assigned to the i-th input unit. The "fundamental difference" among many attribution algorithms is that different attribution algorithms correspond to different allocation ratios .

Table 1 shows how fourteen different attribution algorithms allocate independent effects and interactive effects.

Chart 1. The fourteen attribution algorithms can be written as independent effects and interactive effects Mathematical paradigm for weighted sum. Among them, ## represents Taylor independent effect and Taylor interaction effect respectively, satisfying

is a refinement of the independent effect 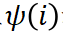and the interactive effect .

Three major criteria for evaluating the reliability of attribution algorithms

In the study of attribution explanation, since it is impossible to obtain/label the true value of neural network attribution explanation, people cannot evaluate the reliability of a certain attribution explanation algorithm from an empirical perspective. The fundamental flaw of "lack of objective evaluation criteria for the reliability of attribution explanation algorithms" has triggered widespread criticism and questioning in the academic field of attribution explanation research.

The revelation of the public mechanism of attribution algorithms in this study enables us to fairly evaluate and compare the reliability of different attribution algorithms under the same theoretical framework. Specifically, we propose the following three evaluation criteria to evaluate whether a certain attribution algorithm distributes independent effects and interactive effects fairly and reasonably.

(1)Guideline 1: Cover all independent effects and interactive effects in the allocation process. After we deconstruct the neural network output into independent effects and interactive effects, a reliable attribution algorithm should cover all independent effects and interactive effects as much as possible in the allocation process. For example, the attribution to the sentence I'm not happy should cover all the independent effects of the three words I'm, not, happy, and also cover J (I'm, not), J (I'm, happy) , J (not, happy), J (I'm, not, happy), etc. all possible interaction effects.

(2)Guideline 2: Avoid assigning independent effects and interactions to irrelevant input units. The independent effect of the i-th input unit should only be assigned to the i-th input unit and not to other input units. Similarly, the interaction effect between input units within the set S should only be assigned to the input units within the set S, and should not be assigned to input units outside the set S (not participating in the interaction). For example, the interaction effect between not and happy should not be assigned to the word I’m.

(3) Guideline three: Complete allocation . Each independent effect (interaction effect) should be fully assigned to the corresponding input unit. In other words, the attribution values ​​assigned to all corresponding input units by a certain independent effect (interaction effect) should add up to exactly the value of the independent effect (interaction effect). For example, the interaction effect J (not, happy) will assign part of the effect (not, happy) to the word not and part of the effect (not, happy) Give the word happy. Then, the distribution ratio should satisfy .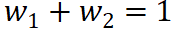

We then used these three evaluation criteria to evaluate the 14 different attribution algorithms mentioned above (as shown in Table 2). We found that the algorithms Integrated Gradients, Expected Gradients, Shapley value, Deep Shap, DeepLIFT Rescale, and DeepLIFT RevealCancel satisfy all reliability criteria.

Table 2. Summary of whether 14 different attribution algorithms meet the three reliability criteria evaluation criteria.

Introduction to the author

The author of this article, Deng Huiqi, is a Ph.D. in applied mathematics from Sun Yat-sen University. During his Ph.D., he worked in the Department of Computer Science at Hong Kong Baptist University and Texas A&M University Visiting student, now conducting postdoctoral research in Zhang Quanshi’s team. The research direction is mainly trustworthy/interpretable machine learning, including explaining the importance of attribution of deep neural networks, explaining the expressive ability of neural networks, etc.

Deng Huiqi did a lot of work in the early stage. Teacher Zhang just helped her reorganize the theory after the initial work was completed to make the proof method and system smoother. Deng Huiqi did not write many papers before graduation. After coming to Teacher Zhang at the end of 2021, he did three tasks in more than a year under the game interaction system, including (1) discovering and theoretically explaining the common representation bottleneck of neural networks, that is, Neural networks have been shown to be even less adept at modeling interactive representations of moderate complexity. This work was fortunate enough to be selected as an ICLR 2022 oral paper, and its review score ranked in the top five (score 8 8 8 10). (2) The theory proves the conceptual representation trend of Bayesian networks and provides a new perspective for explaining the classification performance, generalization ability and adversarial robustness of Bayesian networks. (3) Theoretically explains the neural network’s ability to learn interactive concepts of different complexity during the training process.

The above is the detailed content of Understand and unify 14 attribution algorithms to make neural networks interpretable. For more information, please follow other related articles on the PHP Chinese website!