NP completely cracked the sheep and lost a sheep?

Recently, the topic "Sheep" has become popular on the Internet. There have been more and more articles about how difficult the second level is and how to pass it. However, the difficulty of the game is discussed from the perspective of computational complexity. The article probably doesn't exist yet, so this time I will also write an article about computational complexity to try.

The game mechanism is relatively simple. Simply put, there are some different types of blocks on the map. Players can choose blocks and put them into their slots (the slots have an upper limit. is a constant), if there are three blocks of the same type in the slot, they will be eliminated. The goal of the game is to eliminate all blocks. The difficulty of the game is that the blocks on the map are stacked. The blocks stacked below cannot be selected. They can only be selected (that is, unlocked) after the blocks above are put into the slots. Sometimes the blocks stacked below are The types are unknown due to being obscured.

In fact, the mechanism of Sheep of a Sheep is very similar to that of some mini-games, and many of these mini-games have been proven to be NP-complete, so we are relatively confident that we can also prove the promotion Having a sheep is NP-complete. Here we give a relatively weak and simple reduction structure to illustrate that the promoted sheep-to-sheep game is NP-complete. The generalization we are talking about here means that the number of block types is not limited to a constant, the blocked block type is determined and known, and the number of slots is fixed at 3 (a similar method can be used if the number of slots is other constants, as long as At the beginning of the game, the player is forced to take a special type of block, which can only be eliminated at the end of the game. During the whole process, this block occupies a slot, which is equivalent to missing a slot). Of course, we do not consider the impact of game props here.

The reduction in this article is mainly plagiarized from the Computational Complexity of Games and Puzzles webpage which proves that the Mah-Jongg game (a game similar to Lianliankan, also called Mahjong in some places) is NP -complete reduction.

We still use the classic NP-complete problem of 3-SAT as the reduction problem. We set up 3 square piles for each variable in the 3-SAT formula, one square pile is used to simulate the assignment of the variable (TRUE or FALSE), one square pile corresponds to the assignment of FALSE, and one pile corresponds to the assignment of TRUE. The stack of assignment blocks for simulated variables has two levels. The first level contains 4 identical blocks corresponding to the variables. The second level contains one block each with variables assigned to TRUE and FALSE and a filling block. The heap of blocks corresponding to the value assigned to FALSE is usually multi-layered (may also be reduced to one layer). The top layer contains two blocks corresponding to the variable assigned to FALSE (for use with the previously assigned block heap), and the lower layer contains the blocks corresponding to the variable assigned to FALSE. Clause squares (corresponding to clauses in which variables appear as not) and filler squares. The structure corresponding to the block heap assigned TRUE is similar. Finally, there is a pile of blocks used to verify the solution. This pile is a multi-layered structure, with the top containing blocks corresponding to clauses, the middle being blocks corresponding to variables, and the bottom being blocks corresponding to clauses.

We use a specific example to describe this reduction, assuming that the instance of 3-SAT is 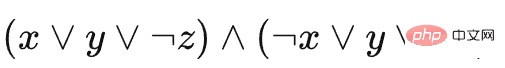. Then the example of the sheep-making-a-sheep game is as follows (in order to express the type and stacking situation of each block, we use the side view to display)

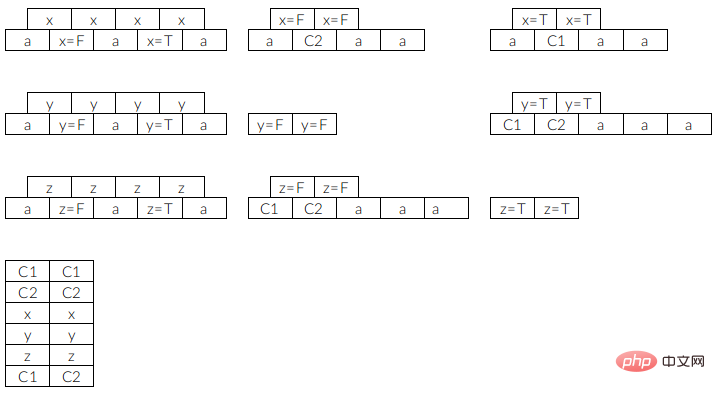
Among them, C1 represents 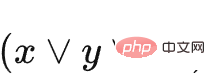, C2 represents 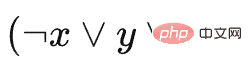, a is a filling square, and square a does not suppress any squares, so it can be left until the end and then all eliminated. Does not affect other blocks. Note that the number of slots we set here is 3, which means that after selecting a certain block and placing it in the slot, you must eliminate this type of block, otherwise the game will not continue.

If the formula can be satisfied, then the blocks can be eliminated according to the assignment of each variable when it is satisfied. For example, assuming that xyz is all assigned FALSE, then we will eliminate the three leftmost x, y, and z. In this way, the second-layer squares x=F, y=F, and z=F will be unlocked, and we can eliminate them. All x=F y=F z=F blocks, then one C1 block and two C2 blocks will be unlocked, and then with the bottom verification block pile, the top two layers of the verification pile can be eliminated, and then the middle variable xyz block will also be unlocked. It can be eliminated immediately, and in the end there is no limit, all blocks can be eliminated.

Conversely, if all the blocks can be eliminated (that is, the level can be passed), then the formula can be satisfied. Note that if the variable xyz block in the verification heap wants to be eliminated, the upper C1 C2 clause blocks must be eliminated first, and the clause block is limited to the assignment block, the assignment block is limited to the variable block, and the placement of the variable block The placement method determines that when assigning values ​​to variables, each variable can only be assigned to one of FALSE or TRUE (specifically, after arbitrarily eliminating 3 of the 4 x squares at the beginning of the game, the squares x=F and x=T There must be one that is not unlocked). This means that the order in which the blocks are eliminated implies an assignment that satisfies the formula.

This means that the necessary and sufficient condition that the 3-SAT formula can satisfy is that the corresponding Sheep of Sheep game instance can be passed. And sheep out of sheep obviously belongs to NP, because it can be determined in polynomial time whether an operation sequence can eliminate all blocks, so we have proved the following proposition:

Proposition: In all Under the condition that the type of blocked block is certain and known, the promoted sheep-le-sheep game is NP-complete.

To put it in non-human terms, you have no way to design an algorithm with polynomial time complexity to determine whether any generalized sheep-to-sheep level has a solution, unless P=NP ( This 4-character equation is worth a land prize and $1 million, so don't sit around trying to prove or disprove it). In human terms, even if the type of blocked block is certain and known, the computer is still (almost) unable to quickly determine whether a sheep can pass the level.

The above is the detailed content of NP completely cracked the sheep and lost a sheep?. For more information, please follow other related articles on the PHP Chinese website!