Comprehensive analysis of large model parameters and efficient fine-tuning, Tsinghua research published in Nature sub-journal

In recent years, Sun Maosong’s team from the Department of Computer Science at Tsinghua University has in-depth explored the mechanism and characteristics of efficient fine-tuning methods for large-scale language model parameters, and collaborated with other relevant teams in the school to complete the research result "Efficient fine-tuning of parameters for large-scale pre-trained language models" (Parameter-efficient Fine-tuning of Large-scale Pre-trained Language Models) was published in "Nature Machine Intelligence" on March 2. The research results were jointly completed by teachers and students from the Department of Computer Science such as Sun Maosong, Li Juanzi, Tang Jie, Liu Yang, Chen Jianfei, Liu Zhiyuan, and Shenzhen International Graduate School Zheng Haitao. Liu Zhiyuan, Zheng Haitao, and Sun Maosong are the corresponding authors of the article and have Ph.D.s in the Department of Computer Science at Tsinghua University. Sheng Dingning (mentor Zheng Haitao) and Qin Yujia (mentor Liu Zhiyuan) are the co-first authors of this article.

Background & Overview

Since 2018, pre-trained language model (PLM) and its "pre-training-fine-tuning" method have become the mainstream paradigm for natural language processing (NLP) tasks , this paradigm first uses large-scale unlabeled data to pre-train a large language model through self-supervised learning to obtain a basic model, and then uses labeled data from downstream tasks to perform supervised learning to fine-tune model parameters to achieve adaptation to downstream tasks.

With the development of technology, PLM has undoubtedly become the infrastructure for various NLP tasks, and in the development of PLM, there is a seemingly irreversible trend: namely Models are getting larger and larger. Larger models will not only achieve better results on known tasks, but also show the potential to complete more complex unknown tasks.

However, larger models also face greater challenges in application. The traditional method of full-parameter fine-tuning of ultra-large-scale pre-trained models consumes a lot of GPU computing. The huge cost of resources and storage resources is prohibitive. This cost has also created a kind of "inertia" in the academic world, that is, researchers only verify their methods on small and medium-scale models, and habitually ignore large-scale models.

In the statistics of this article, we randomly selected 1,000 papers from the last five NLP conferences and found that the use of pre-trained models has become the basic paradigm of research, but it involves large models. But there are very few (as shown in Figure 1).

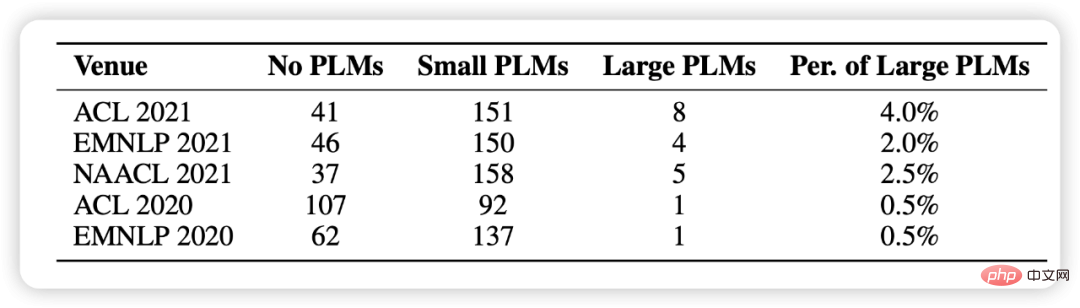
Figure 1: Statistical distribution using pre-trained models among 1000 randomly selected papers

In this context, a new model adaptation scheme, Parameter-efficient method gradually Attracting attention, compared with standard full-parameter fine-tuning, these methods only fine-tune a small part of the model parameters while leaving the rest unchanged, greatly reducing computing and storage costs, while still having performance comparable to full-parameter fine-tuning. We believe that these methods are essentially adjusted on an "increment" (Delta Paremters), so we named it Delta Tuning.

In this paper, we define and describe the Delta Tuning problem, and review previous research through a unified framework. In this framework, existing delta tuning methods can be divided into three groups: incremental (Addition-based), specification-based (Specification-based) and reparameterization (Reparameterization) methods.

In addition to practical significance, we believe that it also has very important theoretical significance. Delta Tuning to some extent reveals the mechanism behind the large model and helps us further develop Theory for large models and even deep neural networks. To this end, we propose a theoretical framework to discuss Delta Tuning from the two perspectives of optimization and optimal control to guide subsequent structure and algorithm design. Furthermore, we conduct a comprehensive experimental comparison of representative methods and demonstrate a comprehensive performance comparison of different methods on results on more than 100 NLP tasks. The experimental results cover the research and analysis of Delta Tuning's performance, convergence performance, efficiency performance, Power of Scale, generalization performance, and migration performance. We also developed OpenDelta, an open source toolkit that enables practitioners to implement Delta Tuning on PLM efficiently and flexibly.

• Paper link: https://www.nature.com/articles/s42256-023-00626-4
• OpenDelta toolkit: https://github.com/thunlp/OpenDelta

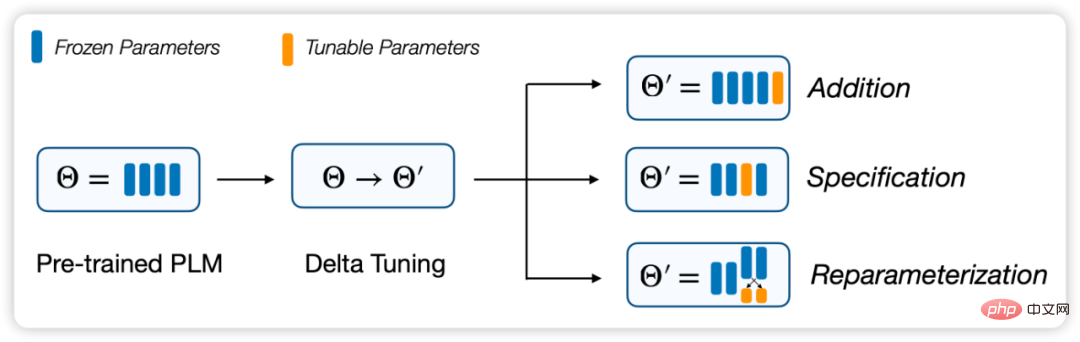
##Figure 2: Division framework of Delta Tuning

Delta Tuning: Method and analysis

Given a pre-trained model and training data, PLM is suitable for The goal of fitting is to generate a model whose parameters are . will be defined as an operation on top of the original model. For traditional full-parameter fine-tuning, there are

, among which

## is the updated value of all parameters in

relative to the training data. In Delta Tuning,

refers to modifying a small number of parameters. Empirically speaking, full-parameter fine-tuning has

, while Delta Tuning has

. Therefore, we can divide parameter-efficient Delta Tuning into three strategies based on the adjusted parameter form and structure, and sort out the previous methods:

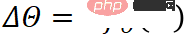
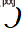
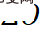
Incremental (Addition- based) methods

This type of method introduces additional trainable neural modules or parameters that are not present in the original model. In this type of approach, based on the above definition, we have

. Common incremental methods include Adapter-Tuning, Prefix Tuning, Prompt Tuning, etc. They invariably insert small-scale neural modules or adjustable parameters into the model, and achieve efficient model adaptation by fine-tuning only this small part of parameters. Among them, Adapter-tuning is the pioneering work of this type of method. It proves that just adding a simple neural network to each layer can be comparable to full-parameter fine-tuning on many tasks. At the same time, Adapter also demonstrates its potential in multi-tasking and multi-language scenarios. Prefix-tuning and Prompt Tuning are very popular delta tuning algorithms recently. They insert some adjustable vectors into the input layer or presentation layer for fine-tuning. Among them, Prompt Tuning can be regarded as a simplified version of Prefix Tuning, that is, only adding Soft Prompt to the input layer. This approach has a very big advantage, that is, there is no need to modify the internal structure of the model. At the same time, as the number of model parameters increases to 10 billion, it has also been proven that it can achieve the same effect as full-parameter fine-tuning on some data. . However, this type of method also faces large optimization problems. Experiments have shown that its optimization efficiency is often lower than other fine-tuning paradigms, takes longer to converge, and performs poorly on small and medium-sized models.

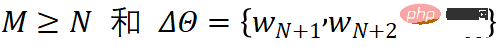
Figure 3: Formal expression of Delta Tuning

Specification-based method

This method specifies that certain parameters in the original model become trainable, while other parameters are frozen. In this type of method, we can represent the training parameter set as , and the updated parameters at this time as . then, the incremental value, otherwise. The specified method does not introduce any new parameters into the model, nor does it seek to change the structure of the model, but directly specifies some parameters to be optimized. The idea is simple but works surprisingly well, for example some methods only fine-tune a quarter of the last layer of BERT and RoBERTa and can produce 90% of the performance of full parameter fine-tuning. A work by BitFit shows that by simply optimizing the bias terms inside the model and freezing other parameters, the model can still reproduce over 95% of the full-parameter fine-tuning performance across multiple benchmarks. Empirical results from BitFit also show that even if we use a small random parameter set for delta tuning (which obviously degrades performance), the model can still produce acceptable results on the GLUE benchmark. Another valuable observation is that different bias terms may have different functions during model adaptation.

In addition to manually or heuristically specifying the parameters to be updated, we can also learn such specification. Diff Pruning is one of the representative works, which reparameterizes the fine-tuned model parameters into the sum of pre-trained parameters and a difference vector, that is. The key issue at this time is to encourage the difference vector to be as sparse as possible. This work regularizes the vector by differentiable approximation to achieve the goal of sparsity. In fact, Diff Pruning consumes more GPU memory than full-parameter fine-tuning due to the introduction of new parameters to be optimized during the learning phase, which may be challenging in applications on large PLMs. The masking method (Masking) learns a selective mask for the PLM, updating only the critical weights for a specific task. To learn such a set of masks, a binary matrix related to the model weights is introduced, where each value is generated by a threshold function. During backpropagation, the matrix is ​​updated by the noise estimator.

Reparameterization-based method

This type of method reparameterizes the existing optimization process into a parameter-valid form by transforming it. Denote the set of parameters to be reparameterized as , and assuming that each is represented by new parameters, then the updated parameters are denoted as , where . Simply put, reparameterization methods are often based on a similar assumption: that the adaptation process of the pre-trained model is inherently low-rank or low-dimensional. This process can therefore be equivalent to a parameter-efficient paradigm.

For example, we can assume that model adaptation has an "intrinsic dimension". By re-parameterizing the fine-tuning process into an optimization process in a low-dimensional subspace, we can simply fine-tune the subspace. parameters within the space to achieve satisfactory performance. In this sense, PLM can serve as a universal compression framework to compress optimization complexity from high to low dimensions. In general, larger PLMs usually have smaller intrinsic dimensions, and the pre-training process implicitly reduces the intrinsic dimensions of the PLM. Inspired by these observations, the reparameterized Delta Tuning method was also proposed, which reparameterizes (part of) the original model parameters using low-dimensional surrogate parameters, optimizing only the surrogate parameters, thereby reducing computational and memory costs.

Another well-known work, LoRA, assumes that changes in weights during model adjustment have a low “intrinsic rank”. Based on this assumption, they propose to optimize low-rank decomposition for changes in the original weight matrix in the self-attention module. In deployment, the optimized low-rank decomposition matrices are multiplied to obtain the increment of the self-attention weight matrix. In this way, LoRA can match the fine-tuned performance on the GLUE benchmark. They demonstrate the effectiveness of their approach on PLMs of various sizes and architectures, even GPT3.

This kind of low-dimensional assumption is not only suitable for single-task adaptation, but can also be extended to multi-task scenarios. IPT assumes that the same low-dimensional eigensubspace exists for multiple tasks, and just adjusting the parameters of the subspace can achieve satisfactory results on more than 100 NLP tasks at the same time. Instead of using random subspaces, this method attempts to find a common subspace that is shared by multiple NLP tasks. Experiments show that in a 250-dimensional low-dimensional subspace, more than 80% of the performance of Prompt Tuning can be reproduced on more than 100 NLP tasks by adjusting only 250 parameters.

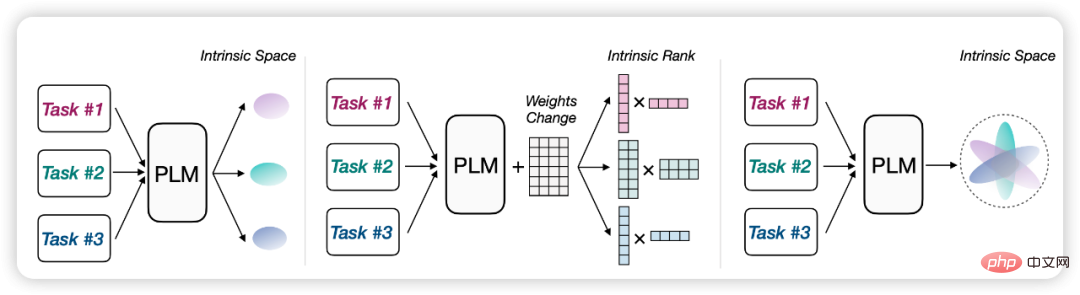
Figure: Re-parameterization methods are often based on similar low-dimensional or low-rank assumptions

Theoretical Perspective of Delta Tuning

Do delta tuning essentially have something in common? We believe that the Delta Tuning method not only has high practical value, but also has far-reaching theoretical significance. They all seem to invariably prove one thing: that is, the adaptation process of large models seems to be a very low-cost process (compared to (for pre-training), it can be done with very little data and very little parameter tuning. The success of Delta Tuning inspired us to further explore the theoretical framework behind model adaptation. This article proposes a framework from two perspectives: Optimization and Optimal Control to conduct a theoretical study of Delta Tuning. interpretation.

Optimization angle

Delta Tuning attempts to achieve the same results on the original large-scale language model by fine-tuning a small number of parameters. Full parameter fine-tuning effect and reduced memory usage. From an optimization perspective, we analyze the effect of Delta Tuning and discuss the design of some Delta Tuning methods under low-dimensional assumptions. After using Delta Tuning, the objective function and the parameters it depends on may change. For the new objective function, only the parameters related to Delta Tuning are optimized. If the initial value is good enough, the performance of the model will not be significantly damaged under certain assumptions. But in order to ensure the effectiveness of Delta Tuning, it is necessary to develop the structure of the problem to design this new objective function. The starting point is to exploit the inherent low-dimensional characteristics of the problem. Generally speaking, there are two ideas that have proven to be useful in practice:

• Find the solution vector in a specific low-dimensional subspace;
• Approximate the objective function in a specific low-dimensional function space.

Because for most applications in deep learning, the objective function usually has many local minimum points, so when the initial value is close to a local minimum point, only a few The search direction is important, or the objective function can be approximated by a simpler function in this neighborhood. Therefore, both optimization ideas are expected to achieve good results, and optimizing low-dimensional parameters is usually more effective and stable.

# Low-dimensional representation of the solution space. Existing research has shown that the parameter optimization of pre-trained language models follows a low-dimensional manifold (Aghajanyan et al., 2021), so this manifold can be embedded into one of the solution vectors low-dimensional representation. If this low-dimensional representation is accurate, then full-parameter fine-tuning on the original model is equivalent to fine-tuning on this low-dimensional parameter. If there is an error in the low-dimensional representation, then when the objective function of the pre-trained model and the new objective function satisfy Lipschitz continuity, the final effect difference between full-parameter fine-tuning and low-dimensional parameter fine-tuning is also controllable.

Some Delta Tuning methods benefit from this design idea. For example, in LoRA (Hu et al., 2021a), the weight matrix adopts low-rank approximation; in BitFit (Zaken et al., 2021) and diff pruning (Guo et al., 2021), only some selected parameters are optimization. The essence of these methods is to update parameters in a smaller subspace of the solution vector, and ultimately achieve better results.

#Low-dimensional representation of function space. Another approach is to directly design an approximation function of the original objective function, and expect the approximate error of this function to be small. Such function approximations can be incremental networks (Houlsby et al., 2019) or augmented feature spaces (Lester et al., 2021). Because we are usually more concerned with the final effect of the language model, it is reasonable to directly consider the approximate effect on the objective function itself.

There are many different ways to construct such function approximations in practice. The simplest is to fix some parameters in the network and only fine-tune the rest. This method expects that part of the network can roughly reflect the performance of the entire network. Because the role of functions in the network is characterized by data flow, a low-rank representation can be injected into the data path in the original network, and the resulting new model is an incremental network, such as an Adapter. The error of the function is determined by the representation power of the delta network.

If the autoregressive structure of Transformer is developed, some more refined function approximations can also be obtained. For example, prompt tuning (Lester et al., 2021) adds a series of prompt tokens as prefixes to the input and only fine-tunes the parameters on which these prompt tokens depend. This method can be regarded as an augmentation of the feature space, and thanks to the properties of Transformer, such a function can better approximate the original function and guide the language model to focus on specific tasks. Related methods include prefix tuning (Li & Liang, 2021). Experiments have observed that prompt tuning has better advantages for larger models and larger data sets. This is also reasonable because these methods essentially use low-dimensional functions to approximate high-dimensional functions. When the scale of the model and data increases, When it is large, there are naturally more degrees of freedom to choose the subspace of function approximation.

Two low-dimensional representations can usually lead to formally similar Delta Tuning methods. (He et al., 2022) made a formally unified statement of Adapter, prefix tuning and LoRA, which can be regarded as viewing various Delta Tuning techniques from the perspective of function approximation. Our discussion shows that these delta tuning methods rely on low-dimensional assumptions. In fact, there are even common low-dimensional subspaces on different tasks (Qin et al., 2021b). Su et al. (2021) and our experimental section also demonstrate the transferability of Delta Tuning across different tasks. Because the actual effect of Delta Tuning is inevitably task-related, in order to achieve the effect of full-parameter fine-tuning, it is beneficial to better explore and utilize the structure of the problem itself or design some hybrid algorithms.

Optimal control perspective

Based on previous theories explaining deep learning from the perspective of optimal control, we start from It is revealed that Delta Tuning can be regarded as a process of finding the optimal controller. For an autoregressive classification model, the model will generate label predictions in the last step (marked as location). This optimization process can be expressed as:

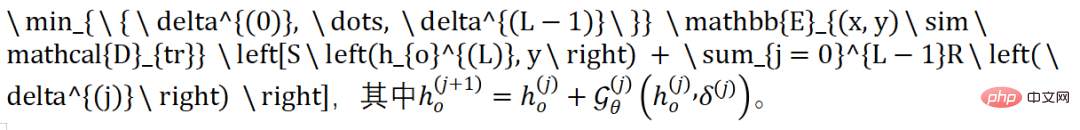
The function here defines the forward propagation of changes in PLM under the intervention of Delta. Specifically, the learnable activations are fixed parameters from so that the representation at layer can be correctly transformed into . Therefore, the representation transformation between two consecutive layers is described by the function and the residual connection in Transformer. Whether it is the Addition-based method of Adapter and Prefix, the specified method of BitFit, or the heavy-parameterization method of LoRA, we can derive such a function to represent Delta Tuning (detailed derivation is in the paper).

We regard the Softmax function and regularization term in Delta Tuning as terminals, and treat the Delta parameter as the operating loss of the control variable, and formulate the Delta Tuning problem as a discrete time control problem , so the forward and backward propagation in Delta Tuning are equivalent to the calculation of the comorphic process in Pontryagin's maximum principle. In summary, incremental tuning can be viewed as the process of seeking the optimal controller for a PLM for a specific downstream task.

Our analysis can inspire the design of novel delta tuning methods, and we also demonstrate that the intervention of delta parameters in PLM is equivalent to the design of the controller. By applying the theory of controller design, we expect to propose more delta tuning methods with theoretical guarantees that the designed delta structure is in principle interpretable under sufficient excitation of PLM.

Comprehensive experimental analysis of Delta Tuning

As an efficient method to inspire and invoke large-scale PLM, Delta Tuning has great potential in various practical application scenarios. In this section, we conduct systematic experiments to gain a deeper understanding of the properties of different mainstream delta tuning methods.

#1. Performance, convergence and efficiency analysis

We first select full-parameter Fine-tuning and four representative Delta Tuning methods (including Prompt Tuning (PT), Prefix-Tuning (PF), LoRA (LR) and Adapter (AP)) provides a thorough comparison of performance, convergence, and efficiency analysis. In order to test more diverse language modeling capabilities, we selected more than 100 typical NLP tasks, including text classification (such as sentiment classification, natural language inference), question answering (such as extractive reading comprehension), language generation (such as text summary) , dialogue) and other tasks, and the input and output of all tasks are modeled into sequence-to-sequence format, so that it is convenient to use the same model (T5) to uniformly model all tasks. Except that PT is tested on T5-base and T5-large, other methods are tested on T5-base.

##Performance Analysis: The experimental results are shown in the table above, we can find that, (1) In general, since different Delta Tuning methods only fine-tune a few parameters, increasing the difficulty of optimization, they cannot match FT in performance in most cases, but the gap between the two is not insurmountable. This demonstrates the potential for large-scale applications of efficient parameter adaptation. (2) Although the design elements of the three methods PF, LR, and AP are different, they are comparable in performance. It is possible for any one of them to perform better than the others (or even FT) on some tasks. Based on the average results, the performance ranking of all methods is FT > LR > AP > PF > PT. At the same time, we also found that the performance of the Delta Tuning method is not consistent with the number of its adjustable parameters, that is, more adjustable parameters will not necessarily bring better performance. In contrast, the specific structural design of Delta Tuning may play a more important role. big effect. (3) PT is the easiest to implement among these methods (that is, it does not modify the internal structure of the model). In most cases, its performance lags far behind other delta tuning methods.

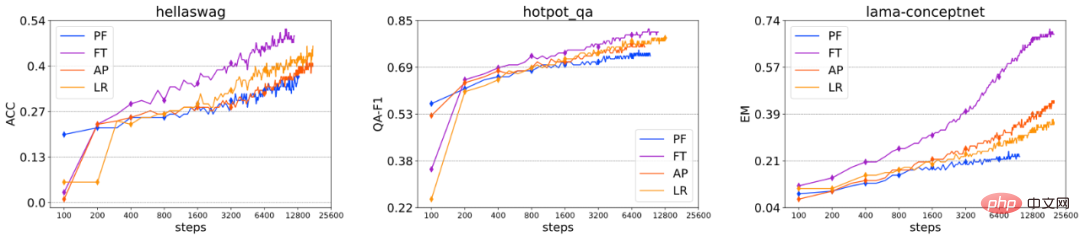
Convergence analysis: We excerpted the performance of different fine-tuning methods on some data sets in different The change in performance under the number of training steps is not included in the above figure because the convergence speed of PT is too slow compared to other methods. We can find that, in general, the order of convergence speed of these fine-tuning methods is: FT > AP ≈ LR > PF. Although PF has the largest number of tunable parameters among all delta tuning methods, it still faces some convergence difficulties, so the convergence speed is not directly related to the number of parameters that can be fine-tuned. In experiments we also found that for each Delta Tuning method, performance and convergence are not sensitive to the number of adjustable parameters, but are more sensitive to the specific structure. Overall, our experiments lead to very similar conclusions in terms of convergence and overall performance, and these conclusions are well supported by results on a large number of datasets.

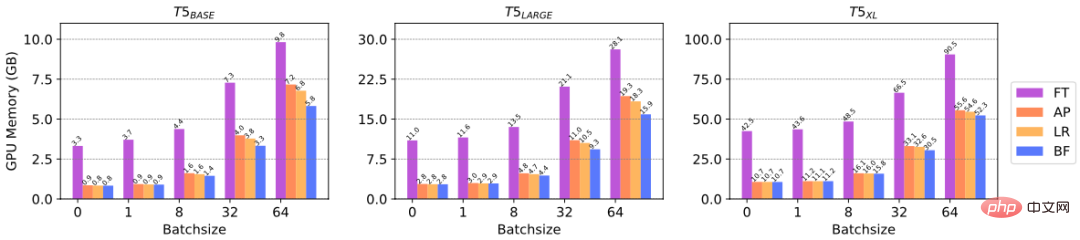
Efficiency Analysis: Delta Tuning can reduce the gradient calculation of parameters, thus saving GPU memory. It reflects the efficiency of computing resources. In order to specifically verify the efficiency improvement of Delta Tuning on GPU memory, we conducted experiments to compare the GPU memory consumed by different Delta Tuning methods for fine-tuning on PLMs of different sizes. Specifically, we selected three scales of T5 models, namely T5-base, T5-large, and T5-xl, and tested the peak GPU memory reached at different batch sizes. We use NVIDIA A100 (maximum GPU memory = 39.58GB) for experiments. From the figure above, we can see that when the batch size is small (for example, 1, 8), Delta Tuning can save up to 3/4 of the GPU memory, and when the batch size is large, Delta Tuning can save at least 1/3 of GPU memory. The above results reflect the efficiency of Delta Tuning in terms of computing resources.

2. Composability analysis

Considering that different Delta Tuning methods are compatible with each other, this means Therefore, they can be applied to the same PLM at the same time. So we investigated whether a combination of Delta Tuning would lead to a performance improvement. Specifically, we explored two combination methods: simultaneous combination and sequential combination, and selected three representative Delta Tuning methods, including Prompt Tuning, BitFit, and Adapter.

Simultaneous combination: We first explore the effect of applying three Delta Tuning methods simultaneously and conduct experiments on 8 GLUE subtasks using RoBERTa-large. We conducted experiments in both full data and low-resource scenarios, and explored the impact of artificial input templates on performance. Artificial templates are designed to bridge the gap between pre-training and downstream task adaptation.

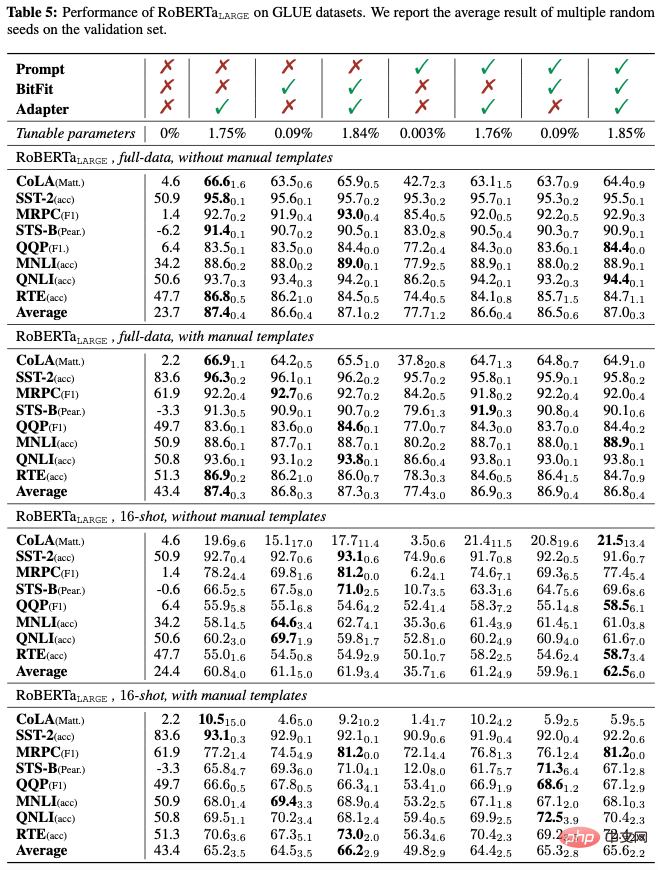
As can be seen from the above table, (1) Whether in full data or low resource scenarios, whether Manual templates exist, and introducing an Adapter in a combination of Delta Tuning almost always helps average GLUE performance; (2) introducing Prompt Tuning in a combination usually hurts average performance, indicating that Prompt Tuning may be incompatible with the other two Delta Tuning methods ; (3) Introducing BitFit into the mix generally improves average performance; (4) Manual templates can significantly improve zero-shot performance (from 23.7 to 43.4) by closing the gap between downstream task adaptation and pre-training. In few-shot settings, artificial templates can also significantly improve average performance. However, when the training supervision signal is relatively abundant (in the full data scenario), the introduction of artificial templates only shows a weak performance improvement, and may even damage the performance.

Sequential combination: In addition to simultaneous combination, we further studied the compatibility of the above three Delta Tuning methods when they are introduced in a certain order. Specifically, we divide the entire fine-tuning into 3 stages. In each stage, we train a separate Delta Tuning method; in the following stage, we fix the Delta Tuning parameters trained in the previous stage unchanged and only optimize the newly introduced Delta Tuning parameters. We conduct experiments on RoBERTa-large with/without artificial templates on the SST-2 sentiment classification dataset. The results are shown in the figure below (excerpt), from which we can conclude that in some cases, the overall performance can be continuously improved by continuously introducing new Delta Tuning methods, thus verifying the advantages of sequential combination; at the same time, we also found , under different settings, there is no fixed optimal combination sequence. The optimal combination may vary due to different downstream tasks, model architecture used, and other factors.

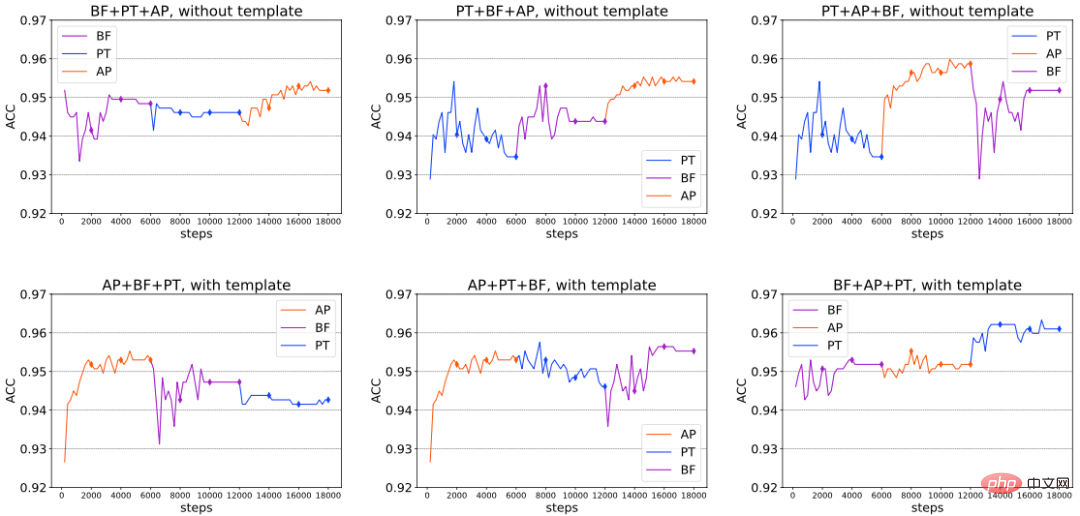
Generalization gap analysis: the memory ability (Memorization) and generalization ability of various fine-tuning methods on training data ( Generalization) are not the same. To this end, we report the generalization gap (training set effect - development set effect) of RoBERTa-large in the full data setting. The results are shown in the table below, from which we can see that (1) Generalization of a single Delta Tuning method The gap is always smaller than Fine-tuning, which means that over-parameterization may help to better memorize (overfit) the training samples. Prompt Tuning tends to have the smallest generalization gap among all delta tuning methods. Considering that each Delta Tuning method can generalize well and show non-trivial performance on the development set, overfitting the training set may not be a necessary condition for good generalization; (2) In general, combining several A Delta Tuning method will increase the generalization gap, even reaching the same level as full Fine-tuning. This shows that remembering the training set (Memorization) may not require too much fine-tuning; in other words, when PLM adapts to downstream tasks, even if the fine-tuning capacity of the model is small, it is still good enough to memorize the training set; (3) Using artificial templates generally does not affect the generalization gap.

3. Performance changes as model size increases

We studied the impact of model size increase on Delta Tuning performance Impact. Recently, some research has found that as the size of the PLM model used increases, the performance of Prompt Tuning will become stronger and stronger, and can even reach a level comparable to full-parameter Fine-tuning fine-tuning. In this section, we explore whether all delta tuning methods exhibit the Power of Scale. Specifically, we conducted experiments on three typical NLP tasks: MNLI, QNLI, and SST-2, and selected three PLMs of increasing scale (T5-small, T5-base, T5-xxl), and evaluated The performance of six representative delta tuning methods (Adapter, LoRA, Prefix-Tuning, Prompt Tuning, Last Layer Tuning and Selective Module Tuning), the results are shown in the figure below.

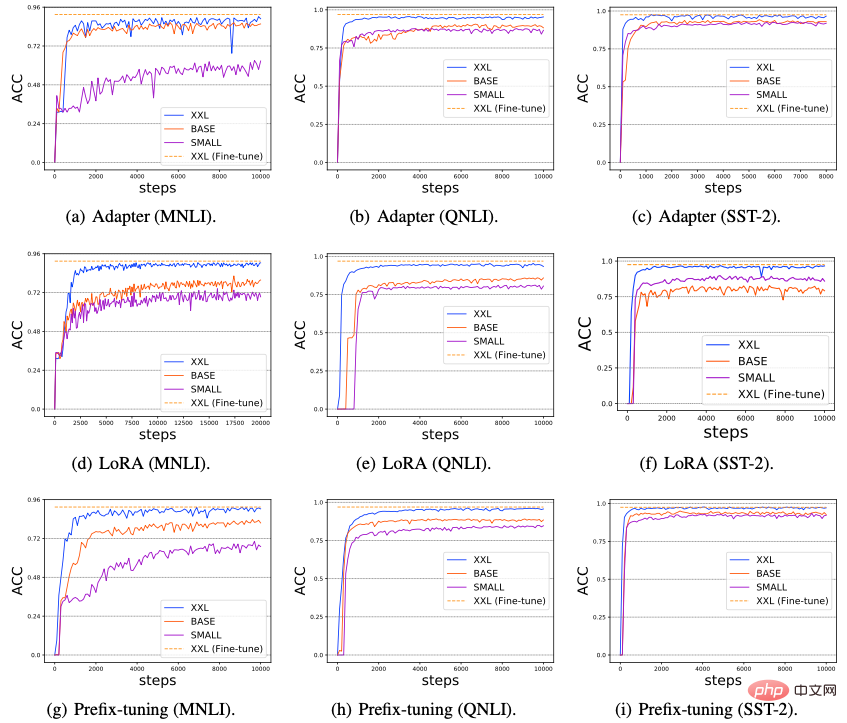
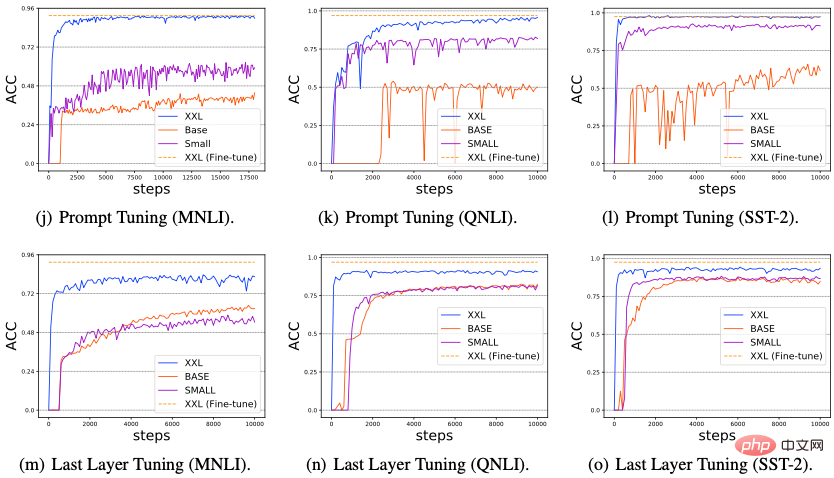
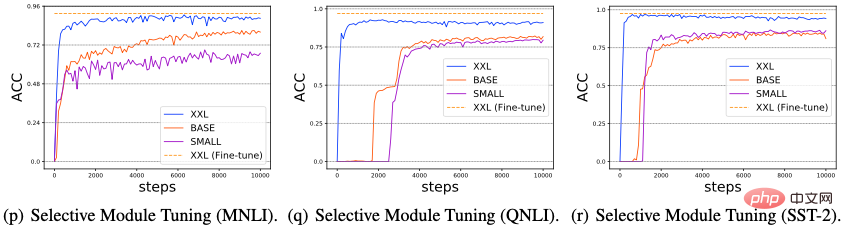
#From Figure (a-i), we can observe that as the PLM network scale grows, the performance and convergence of all Delta Tuning methods are significantly improved; (2) In addition ,Figure (j-l) shows that compared with other delta ,tuning methods, Prompt Tuning tends to perform poorly ,on small-scale PLMs (T5-small and T5-base). However, other Delta Tuning methods do not have this problem; (3) Based on the existing results, in Figure 11 (m-o) and (p-r), we further design two Delta Tuning methods: Last Layer Tuning and Selective Module Tuning. For Last Layer Tuning, we only fine-tune the last layer of the T5 encoder; for Selective Module Tuning, we randomly select some modules in the T5 model for fine-tuning. Both methods show excellent results, especially when the scale of PLM is very large, with Selective Module Tuning slightly better than Last Layer Tuning. These results suggest that limiting fine-tunable parameters to a specific layer may not be a good strategy. On the other hand, when the scale of PLM becomes very large, fine-tuning by randomly selecting modules across different layers can achieve excellent performance. Overall, the above results indicate that as the PLM model size grows, significant improvements in performance/convergence speed of various fine-tuning methods may be a common phenomenon in Delta Tuning. We speculate that this phenomenon exists because larger PLMs usually have smaller intrinsic dimensions (Intrinsic Dimension). Therefore, only adjusting a few parameters can obtain strong enough representation capabilities to implement in downstream tasks. Non-trivial performance; in addition, over-parameterized models may be less likely to fall into local optima during downstream optimization, thus accelerating convergence.

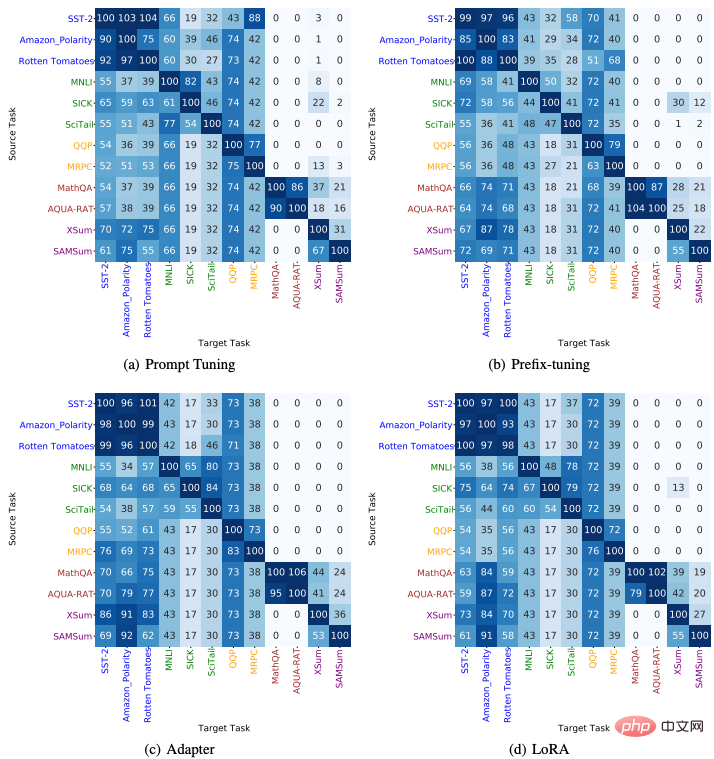
4. Inter-task migration capability

We studied the transferability of the Delta Tuning method between different downstream tasks Specifically, we used 4 Delta Tuning methods (Prompt Tuning, Prefix-Tuning, Adapter and LoRA) and 12 NLP tasks of 5 different types (including sentiment analysis, natural language reasoning, paraphrase recognition, question answering, Summary), and transfer the Delta parameters trained on the source task to the target task to test the zero-shot transfer effect. The results are shown in the figure below, from which we can observe: (1) For tasks belonging to the same category, the transfer between them usually performs well; (2) For tasks of different types, the transfer performance between them is poor; ( 3) In addition, we found that the Delta parameters trained from text generation tasks (such as question and answer and summarization) can be transferred to sentiment analysis tasks and achieve excellent performance, which indicates that the text generation task may be a more complex task to solve. The language skills required for the task may include sentiment analysis skills.

## Application of Delta Tuning

Fast training and storage space saving. Transformer models, while inherently parallelizable, are very slow to train due to their sheer size. Although the convergence rate of Delta Tuning may be slower than traditional full-parameter fine-tuning, the training speed of Delta Tuning is also significantly improved as the computational effort of fine-tunable parameters during backpropagation is significantly reduced. Previous research has verified that using Adapters for downstream tuning can reduce training time to 40% while maintaining performance comparable to full parameter fine-tuning. Due to its lightweight nature, the trained Delta parameters can also save storage space, thereby facilitating sharing among practitioners and promoting knowledge transfer.

Multi-task learning. Building general artificial intelligence systems has long been a goal of researchers. Recently, very large PLMs (e.g., GPT-3) have demonstrated the amazing ability to simultaneously fit different data distributions and facilitate downstream performance on a variety of tasks. Therefore, in the era of large-scale pre-training, multi-task learning has received more and more attention. As an effective alternative to full-parameter fine-tuning methods, Delta Tuning has excellent multi-task learning capabilities while maintaining relatively low additional storage. Successful applications include multi-language learning, reading comprehension, and more. Additionally, Delta Tuning is also expected to serve as a potential solution to catastrophic forgetting in continuous learning. The language abilities acquired during pre-training are stored in the parameters of the model. Therefore, updating all parameters in the PLM without regularization may lead to severe and catastrophic forgetting when the PLM is trained sequentially across a sequence of tasks. Since Delta Tuning only tunes minimal parameters, it could be a potential solution to mitigate the catastrophic forgetting problem.

Centralized model service and parallel computing. Very large PLM is often released as a service, that is, users consume the large model by interacting with APIs published by the model provider, rather than storing the large model locally. Considering the unbearable communication cost between users and service providers, Delta Tuning is clearly a more competitive option than traditional full-parameter fine-tuning due to its lightweight nature. On the one hand, service providers can support the downstream tasks required to train multiple users while consuming less computing and storage space. In addition, considering that some Delta Tuning algorithms are inherently parallelizable (such as Prompt Tuning and Prefix-Tuning, etc.), Delta Tuning can allow parallel training/testing of samples from multiple users in the same batch (In-batch Parallel Computing). Recent work has also shown that most delta tuning methods, if not inherently parallelizable, can be modified in some ways to support parallel computation. On the other hand, when the gradients of the central model are not available to the user, Delta Tuning is still able to optimize large PLMs through a gradient-free black-box algorithm and only calls to the model inference API.

The above is the detailed content of Comprehensive analysis of large model parameters and efficient fine-tuning, Tsinghua research published in Nature sub-journal. For more information, please follow other related articles on the PHP Chinese website!