Home >Technology peripherals >AI >Predicting discrete-time bifurcations through deep learning
Predicting discrete-time bifurcations through deep learning
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-07-16 21:27:51794browse

Many natural and man-made systems are prone to critical transitions – sudden and potentially damaging changes in dynamics. Deep learning classifiers can provide early warning signals for critical transitions by learning common features of bifurcations from large simulated training data sets. So far, classifiers have only been trained to predict continuous-time bifurcations, ignoring the rich dynamics that characterize discrete-time bifurcations.
Here, Thomas M. Bury's research team at McGill University trained a deep learning classifier to provide early warning signals for five local discrete-time bifurcations of codimension one. They tested the classifier using simulated data from discrete-time models used in physiology, economics and ecology, as well as experimental data from spontaneously beating chicken heart aggregates undergoing period-doubling bifurcation.
Across various noise intensities and close bifurcation rates, this classifier exhibits higher sensitivity and specificity than commonly used early warning signals. It can also predict the correct bifurcation in most cases, with particularly high accuracy for period-doubling bifurcations, Neimark-Sacker bifurcations, and folding bifurcations.
The research was titled "Predicting discrete-time bifurcations with deep learning" and was published in "Nature Communications" on October 10, 2023.
- Critical Transitions:
- The critical threshold at which a system experiences sudden, significant dynamic changes.
- For example: heart rhythm changes, financial market collapse, ecosystem collapse.
- Bifurcation theory:
- Study of dynamical systems that undergo qualitative changes at thresholds.
- Accompanied by local stability weakening (slowing down), resulting in changes in noise time series properties.
- These changes are available for critical transitions of EWS.
- Existing EWS:
- Variance and lag 1 autocorrelation changes ahead of transitions in climate, geology, ecology and cardiac systems.
- Prediction capabilities are limited and may fail in some systems.
- Deep Learning EWS:
- Train a neural network to predict bifurcation types based on time series.
- Learn universal features from databases with bifurcated simulations.
- Suitable for invisible time series due to the universal properties of bifurcation.
Discrete-time bifurcated EWS
- Discrete-time dynamical systems exhibit different behavior from continuous-time dynamical systems.
- Discrete time bifurcations occur naturally in physiology, epidemiology and economics.
- The researchers tested the performance of deep learning classifiers in discrete-time bifurcations using simulated and experimental data.
Periodic doubling bifurcation:
- Type of discrete-time bifurcation where events occur alternately at intervals.
- Along with the slowdown, there are systematic changes in variance and lag 1 autocorrelation.
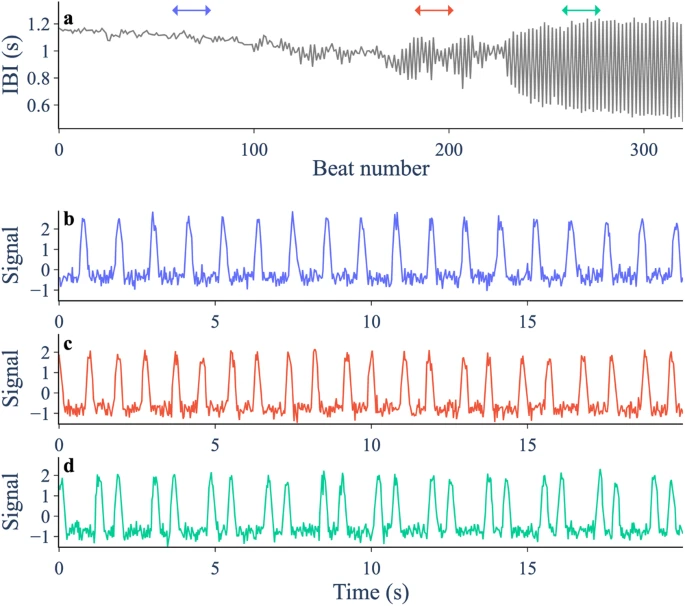
- Has been observed experimentally in chicken heart aggregates and in human hearts and can be used in EWS.
Illustration: After treatment with a potassium channel blocker (E-4031, 1.5 μmol), spontaneously beating embryonic chicken heart cell aggregates exhibit period-doubling bifurcation. (Source: Paper)
Discrete-time bifurcation
There are many types of discrete-time bifurcation, each with associated dynamic changes. In the latest study, the Bury team focused on five local bifurcations of codimension one. In the "local" case, these bifurcations are accompanied by severe slowdowns, so systematic variation, variance and autocorrelation are expected.
Types of Predicted Bifurcations
However, not all of these divergences lead to critical transitions. Instead, they can transition smoothly to intersecting steady states (transcritical) or to oscillations of gradually increasing amplitude (supercritical Neimark-Sakr). Predicting the bifurcation type provides information about the nature of the post-bifurcation dynamics that variance and autocorrelation alone cannot provide.
Deep Learning Classifier
The team trains a deep learning classifier to provide specific EWS for bifurcations of discrete-time dynamic systems. They trained the classifier using simulated data from normalized equations appended with higher-order terms and noise.
Classifier testing
The team then tested the classifier on simulated runs of five discrete-time models used in cardiology, ecology and economics, and assessed its relative variance and lag 1 autocorrelation performance. The robustness of the EWS is assessed by varying the noise amplitude and forcing rate in model simulations.
Experimental validation
Finally, the researchers tested the classifier using experimental data from spontaneously beating chicken heart aggregates undergoing period-doubling bifurcation.
Paper link:
https://www.nature.com/articles/s41467-023-42020-z
The above is the detailed content of Predicting discrete-time bifurcations through deep learning. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Technology trends to watch in 2023
- How Artificial Intelligence is Bringing New Everyday Work to Data Center Teams
- Can artificial intelligence or automation solve the problem of low energy efficiency in buildings?
- OpenAI co-founder interviewed by Huang Renxun: GPT-4's reasoning capabilities have not yet reached expectations
- Microsoft's Bing surpasses Google in search traffic thanks to OpenAI technology