LLM | Yuan 2.0-M32: Expert Mixture Model with Attention Routing

Picture

1. The conclusion is written in front

Yuan+2.0-M32 is a This infrastructure is similar to Yuan-2.0+2B, using an expert hybrid architecture containing 32 experts. 2 of these experts are active. An expert hybrid architecture containing 32 experts is proposed and adopted to select experts more efficiently. Compared with the model using the classic routing network, the accuracy rate is increased by 3.8%. Yuan+2.0-M32 is trained from scratch, using 2000B tokens, and its training consumption is only 9.25% of that of a dense ensemble model of the same parameter size. In order to better select experts, the attention router is introduced, which has the ability to sense quickly and thus enable better selection of experts.

Yuan 2.0-M32 has demonstrated competitive capabilities in coding, mathematics and multiple professional fields, using only 3.7 billion active parameters out of 40 billion total parameters, and 7.4 GFlops per token. Calculated forward, both indicators are only 1/19 of Llama3-70B. Yuan 2.0-M32 surpassed Llama3-70B in the MATH and ARC-Challenge benchmarks, with accuracy rates reaching 55.89% and 95.8% respectively. The model and source code of Yuan 2.0-M32 are on GitHub: https://github.com/IEIT-Yuan/Yuan2.0-M32.

2. Brief introduction of the paper

2.1 Background of the paper

In each token With a fixed amount of computation, a model using a mixture of experts (MoE) structure can easily be built larger than a dense set model by increasing the number of experts, thereby achieving higher accuracy performance. In fact, when training models with limited computing resources, MoE is seen as an excellent option to reduce the costs associated with model, dataset size and limited computing power.

The concept of MoE (Mixture of Experts) can be traced back to 1991. The total loss is a combination of weighted losses from each expert who has the ability to make independent judgments. The concept of sparsely gated MoE was originally proposed by Shazeer et al. (2017) in translation models. Using this routing strategy, only a few experts are activated when raising questions, rather than all experts being called at the same time. This sparsity allows the model to scale up to 1000 times between stacked LSTM layers with minimal loss in computational efficiency. Noise-adjustable Top-K gating routing introduces adjustable noise to the softmax function from the network and maintains the K value to balance expert utilization. In recent years, with the continuous expansion of model scale, routing strategies have received more attention in efficiently allocating computing resources.

The expert routing network is the core of the MoE structure. This structure selects candidate experts to participate in the calculation by calculating the probability of token assignment to each expert. Currently, in most popular MoE structures, the classical routing algorithm is commonly used, which performs the dot product between the token and the feature vector of each expert and selects the expert with the largest dot product as the winner. In this choice, the feature vectors of experts are independent and the correlation between experts is ignored. However, the MoE structure usually selects more than one expert at a time, and there may be correlations between the characteristics of different experts. Therefore, in this case, the selected feature vectors may have overlaps and conflicts for the dot products between each expert involved in the calculation, which in turn affects the accuracy of the results. However, the MoE structure usually selects more than one expert at a time, and there may be correlations between the features of different experts. Therefore, in this case, the feature vectors selected by the classic routing algorithm may overlap and conflict, affecting the calculation accuracy. To solve this problem, MoE structures often adopt independent expert feature vectors, which means that each expert is treated as completely independent, while the correlation between experts is ignored. However, this approach can cause some problems. Therefore, when selecting experts, the MoE structure usually selects more than one expert, and there may be correlations between the characteristics of different experts. In this case, the selected feature vectors may have overlaps and conflicts for the dot products between each expert involved in the calculation, which in turn affects the accuracy of the results. Therefore, the MoE structure requires a more accurate routing algorithm to select the best experts, and the selection needs to be considered

2.2 Method of the paper

2.2.1 Model Architecture

Based on the model structure of Yuan 2.0-2B, Yuan 2.0 introduces local filtering-based attention (LFA) to consider the local dependence of the input token , thereby improving the accuracy of the model. In Yuan 2.0-M32, the dense feed-forward network (FFN) of each layer is replaced with MoE components.

Figure 1 shows the architecture of the MoE layer applied in the paper model. Taking four FFNs as an example (actually there are 32 experts), each MoE layer consists of an independent FFN as an expert. Since the expert path network assigns input tokens to relevant experts, the classic path network establishes a feature vector for each expert. And calculate the dot product between the input token and each expert feature vector to obtain the similarity between the token and each expert. The expert with the highest similarity will be used to calculate the output. The expert with the strongest similarity is selected for activation and participates in subsequent calculations.

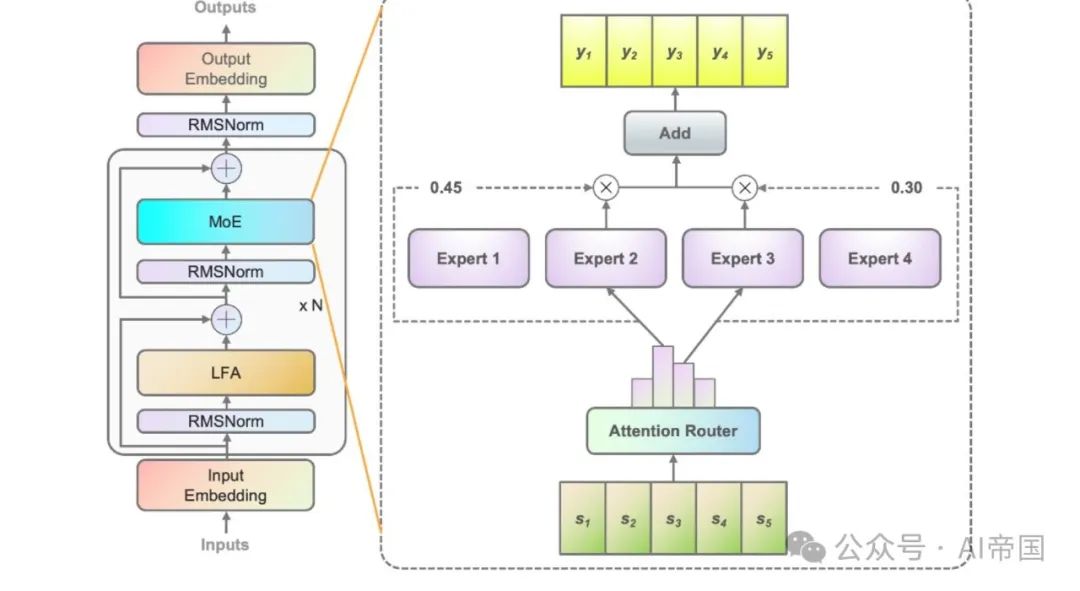Picture

图 1: An explanation of Yuan 2.0-M32. The picture on the left shows the expansion of the MoE layer in the Yuan 2.0 architecture. The MoE layer replaces the feedforward layer in Yuan 2.0. The figure on the right shows the structure of the MoE layer. In the paper's model, each input token will be assigned to 2 of a total of 32 experts, while in the figure the paper uses 4 experts as an example. The output of the MoE is the weighted sum of the selected experts. N represents the number of layers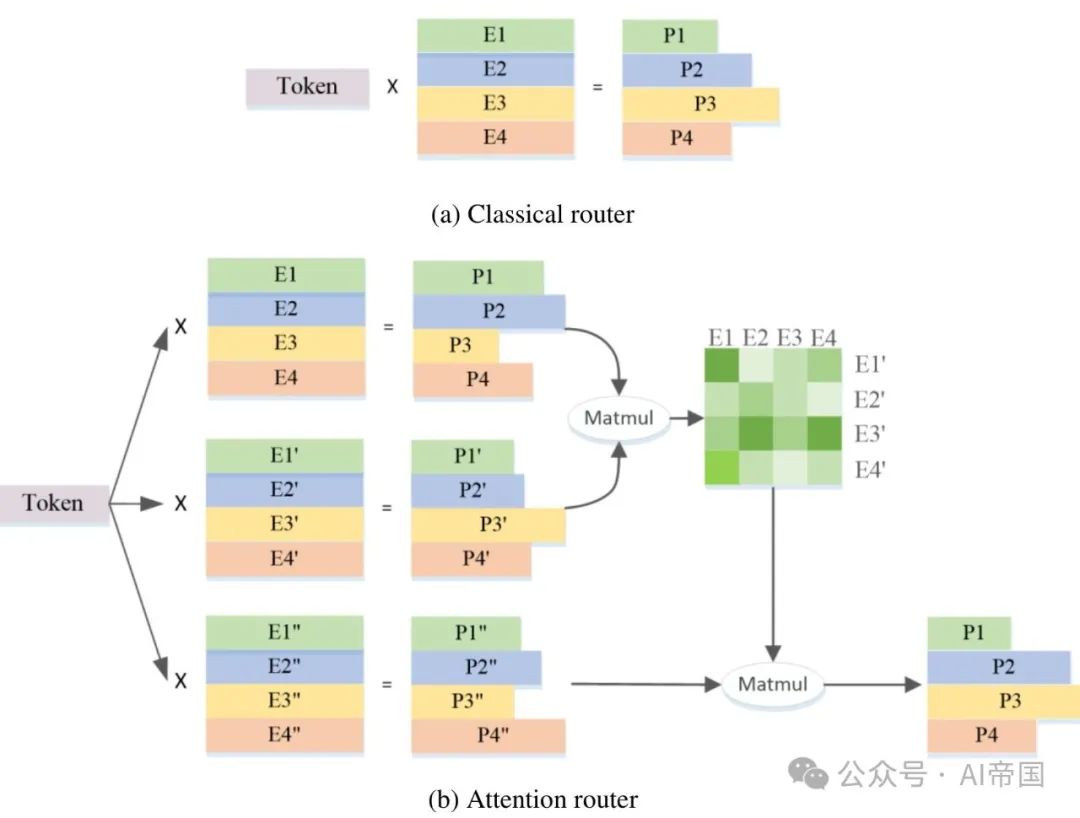
Figure 2 shows an overview of the attention router structure

Figure 2(a) shows the structure of a classic routing network. The feature vectors of each expert are independent of each other, and the correlation between experts is ignored when calculating the probability. In fact, in most MoE models, two or more experts are usually selected to participate in subsequent calculations, which naturally brings about strong correlation between experts. Taking into account inter-expert correlations certainly helps improve accuracy.

Figure 2(b) shows the architecture of the attention router proposed in this work. This novel routing network integrates the correlation between experts by adopting the attention mechanism. A coefficient matrix representing the correlation between experts is constructed and applied in the calculation of the final probability value.

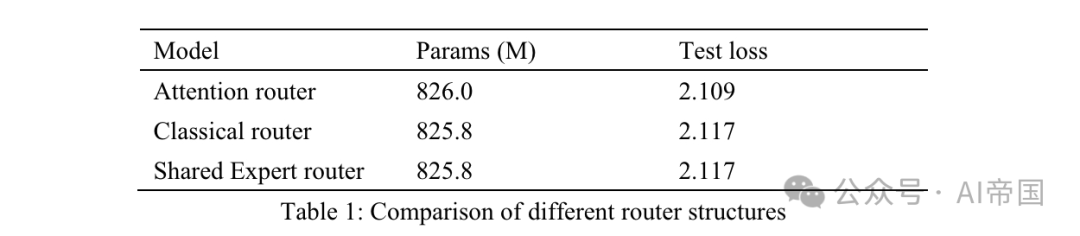Table 1: Comparison of different routing structures

Table 1 lists the accuracy results of different routers. The paper's model tested the attention router on 8 trainable experts. The classic router model has 8 trainable experts to ensure similar parameter scale, and the routing structure is the same as that applied to Mixtral 8*7B, i.e. Softmax on one linear layer. The shared expert router adopts the shared expert isolation strategy and classic routing architecture. There are two fixed experts capturing general knowledge, and the first two of the 14 optional experts as specialized experts.

The output of MoE is a combination of fixed experts and experts selected by the router. All three models use 30Btokens for training and another 10Btokens for testing. Considering the results between the classic router and the shared expert router, the paper found that the latter achieved exactly the same test loss with a 7.35% increase in training time. The computational efficiency of shared experts is relatively low and does not lead to better training accuracy than the classic MOE strategy. Therefore, in the paper's model, the paper adopts a classic routing strategy without any shared experts. Compared with the classic routed network, the test loss of attention router increased by 3.8%.

The paper tests the scalability of the model by increasing the number of experts and fixing the parameter size of each expert. Increasing the number of training experts only changes the model capacity, not the actual activated model parameters. All models are trained with 50 billion tokens and tested with an additional 10 billion tokens. The paper sets the activated experts to 2, and the training hyperparameters of the three models are the same. The expert scaling effect is measured by the test loss after training 50 billion tokens (Table 2). Compared to the model with 8 trainable experts, the model with 16 experts showed a 2% loss reduction, while the model with 32 experts showed a 3.6% loss reduction. Considering its accuracy, the paper selected 32 experts for Yuan 2.0-M32.

Table 2: Extended experimental results

2.2.2 Model training

Yuan 2.0-M32 trains with a combination of data parallelism and pipeline parallelism, but does not use tensor parallelism or optimizer parallelism. Figure 3 shows the loss curve, and the final training loss is 1.22.

Figure 3: Pre-training loss of Yuan2.0-M32 on 2000Btoken

             

2.2.3 Fine-tuning

During the fine-tuning process, the paper extended the sequence length to 16384. Following the work of CodeLLama (Roziere et al., 2023), the paper resets the fundamental frequency value of the rotated position embedding (RoPE) to avoid the attenuation of the attention score as the sequence length increases. Rather than simply increasing the base value from 1000 to a very large value (e.g. 1000000), the paper uses NTK awareness (bloc97, 2023) to calculate the new base value.

The paper also compares the performance of the pre-trained Yuan 2.0-M32 model with the new base value of the NTK perceptual style, and with other base values ​​in the needle retrieval task with sequence lengths up to 16K. The paper finds that the new base value of 40890 for the NTK perceptual style performs better. Therefore, 40890 was applied during fine-tuning.

2.2.4 Pre-training data set

Yuan 2.0-M32 is pre-trained from scratch using a bilingual data set containing 2000B tokens. The pre-trained raw data contains over 3400B tokens, and the weight of each category is adjusted based on data quality and quantity.

The comprehensive pre-training corpus consists of the following:

44 sub-datasets, covering web crawled data, Wikipedia, and academic papers , books, code, math and formulas, and domain-specific expertise. Some of them are open source datasets and the rest were created by Yuan 2.0.

Some common web crawler data, Chinese books, conversations and Chinese news data are inherited from Yuan 1.0 (Wu et al., 2021). Most of the pre-training data in Yuan 2.0 has also been reused.

Details about the construction and sources of each dataset are as follows:

Network (25.2%): Website crawler data is obtained from open source The dataset and paper were collected from public crawler data processed in previous work (Yuan 1.0). For more details on the Massive Data Filtering System (MDFS) for extracting high-quality content from web context, please refer to Yuan 1.0.

Encyclopedias (1.2%), papers (0.84%), books (6.49%) and translations (1.1%): Data are inherited from the Yuan 1.0 and Yuan 2.0 datasets.

Code (47.5%): The code dataset has been greatly expanded compared to Yuan 2.0. The paper uses code from Stack v2 (Lozhkov et al., 2024). Comments in Stack v2 are translated into Chinese. Code synthesis data were generated via a similar approach to Yuan 2.0.

Mathematics (6.36%): All math data from Yuan 2.0 has been reused. These data mainly come from open source datasets, including proof-pile vl (Azerbayev, 2022) and v2 (Paster et al., 2023), AMPS (Hendrycks et al., 2021), MathPile (Wang, Xia, and Liu, 2023 ) and StackMathQA (Zhang, 2024). Created a synthetic data set for numerical calculations using Python to facilitate four arithmetic operations.

Specific domain (1.93%): This is a dataset containing different background knowledge.

2.2.5 Fine-tuning data set

The fine-tuning data set is extended based on the data set applied in Yuan 2.0.

Code instruction data set. All programming data with Chinese instructions and some with English comments are generated by large language models (LLMs). About 30% of the code instruction data is in English, and the rest is in Chinese. The synthetic data mimics Python code with Chinese annotations in prompt generation and data cleaning strategies.

Python code with English comments is collected from Magicoder-Evol-Instruct-110K and CodeFeedback-Filtered-Instruction. Extract instruction data with language tags (such as "python") from the dataset.

Codes in other languages ​​such as C/C++/Go/Java/SQL/Shell, with English comments, are derived from open source data sets and are processed in a similar way to Python code. The cleaning strategy is similar to the method in Yuan 2.0. A sandbox is designed to extract compilable and executable lines from the generated code and retain lines that pass at least one unit test.

Mathematical instruction data set. The math instruction data sets are all inherited from the fine-tuning data set in Yuan 2.0. In order to improve the model's ability to solve mathematical problems through programming methods, the paper constructed mathematical data prompted by Thoughts (PoT). PoT converts mathematical problems into code generation tasks that perform calculations in Python.

Safety instruction data set. In addition to the Yuan 2.0 chat data set, the paper also builds a bilingual safety alignment data set based on an open source safety alignment data set. The paper only extracts questions from public data sets, increases the diversity of questions, and uses large language models to regenerate Chinese and English answers.

2.2.6 Tokenizer

For Yuan 2.0-M32, the English and Chinese tokenizers are inherited from the tokenizer applied in Yuan 2.0.

2.3 The effect of the paper

The paper evaluates the code generation capability of Yuan 2.0-M32 on HumanEval, and evaluates it on GSM8K and MATH Mathematical problem solving, which assesses scientific knowledge and reasoning skills on the ARC and as a composite benchmark on the MMLU.

2.3.1 Code Generation

The code generation capabilities are evaluated using the HumanEval benchmark. Assessment methods and tips are similar to those mentioned in Meta 2.0.

Table 3: Comparison between Yuan 2.0-M32 and other models on HumanEval pass @1

The model is expected to complete the function after. The generated functions will be evaluated through unit tests. Table 3 shows the results of Yuan 2.0-M32 in zero-shot learning and compares it with other models. The results of Yuan 2.0-M32 are second only to DeepseekV2 and Llama3-70B, and far exceed those of other models, even though its active parameters and computational consumption are much lower than other models.

Compared with DeepseekV2, the model of the paper uses less than one-quarter of the active parameters, and the calculation amount per token is less than one-fifth of it, while achieving more than 90% accuracy level. Compared with Llama3-70B, the gap between model parameters and calculation amount is even greater, but the paper can still reach 91% of its level. Yuan 2.0-M32 demonstrated solid programming ability, passing three out of four questions. Yuan 2.0-M32 excels at small sample learning, increasing HumanEval's accuracy to 78.0 in 14 attempts.

2.3.2 Mathematics

Yuan 2.0-M32’s mathematical capabilities are evaluated through GSM8K and MATH benchmarks. The prompts and testing strategies for GSM8K are similar to those applied to Yuan 2.0, with the only difference being that the paper uses 8 attempts (Table 4).

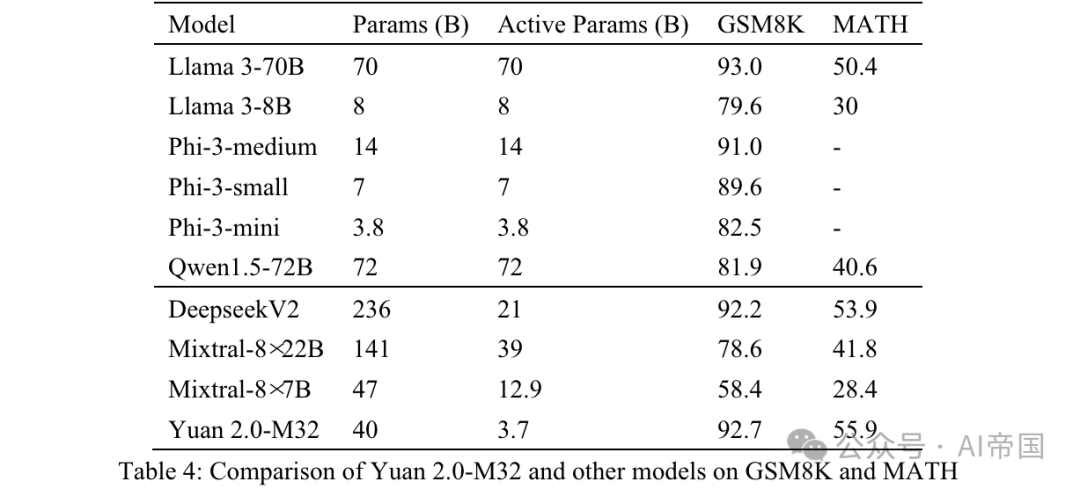Table 4: Comparison between Yuan 2.0-M32 and other models on GSM8K and MATH

MATH is a model containing 12, A dataset of 500 challenging mathematics competition question questions. Each question in this dataset has a complete step-by-step solution, guiding the model to generate answer derivation and explanations. The answer to the question can be a numerical value, or a mathematical expression (such as y=2x+5, x-+2x-1, 2a+b, etc.). Yuan 2.0-M32 uses the Chain of Thinking (CoT) method to generate the final answer through 4 attempts. Answers will be extracted from the analysis and converted into a unified format.

For numerical results, mathematically equivalent output in all formats is accepted. For example, the fractions 1/2, 12, 0.5, 0.50 are all converted to 0.5 and treated as the same result. For mathematical expressions, the paper removes tab and space symbols and unifies regular expressions for rhythm or musical notes. 55 '5' are all accepted as the same answer. The final result after processing is compared with the standard answer and evaluated using EM (Exact Match) score.

As can be seen from the results shown in Table 4, Yuan 2.0-M32 has the highest score on the MATH benchmark. Compared with Mixtral-8x7B, the latter's active parameters are 3.48 times that of Yuan 2.0-M32, but Yuan's score is almost twice that. On GSM8K, the Yuan 2.0-M32's score is also very close to the Llama 3-70B and better than the other models.

2.3.3MMLU

Large-scale multi-task language understanding (MMLU) covers 57 disciplines such as STEM, humanities, and social sciences. Ranging from basic language tasks to advanced logical reasoning tasks. All questions in MMLU are multiple-choice QA questions in English. The model is expected to generate the correct options or corresponding analyses.

The input data organization of Yuan 2.0-M32 is shown in Appendix B. The previous text is sent to the model and all answers related to the correct answer or option label are considered correct.

Final accuracy is measured by MC1 (Table 5). The results on MMLU demonstrate the capabilities of the paper model in different fields. Yuan 2.0-M32 exceeds Mixtral-8x7B, Phi-3-mini and Llama 3-8B in performance.

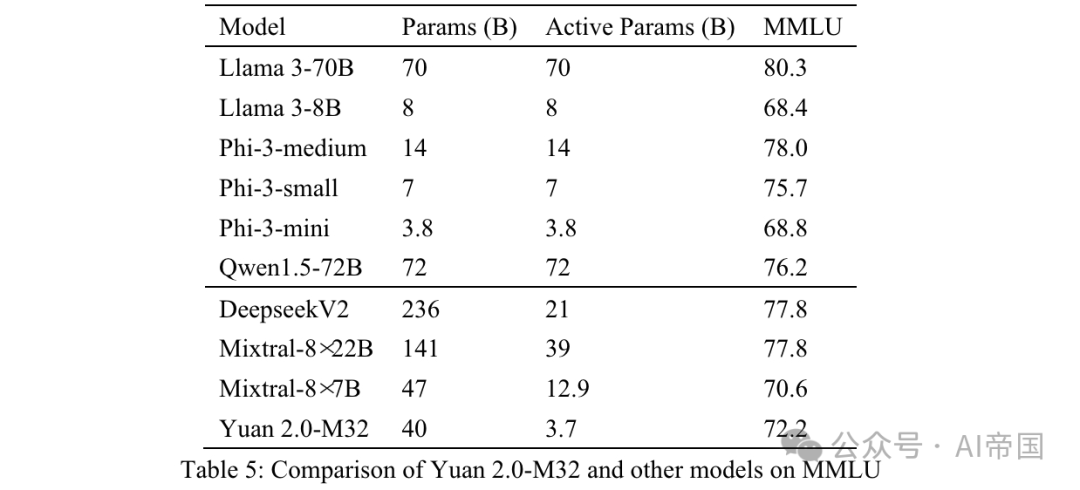Table 5: Comparison of Yuan 2.0-M32 and other models on MMLU

2.3.4 ARC

The AI2 Reasoning Challenge (ARC) benchmark is a multi-choice QA dataset containing questions from 3rd to 9th grade science exams. It is divided into two parts: Easy and Challenge, with the latter containing more complex parts that require further reasoning. The paper tests the paper's model in the challenges section.

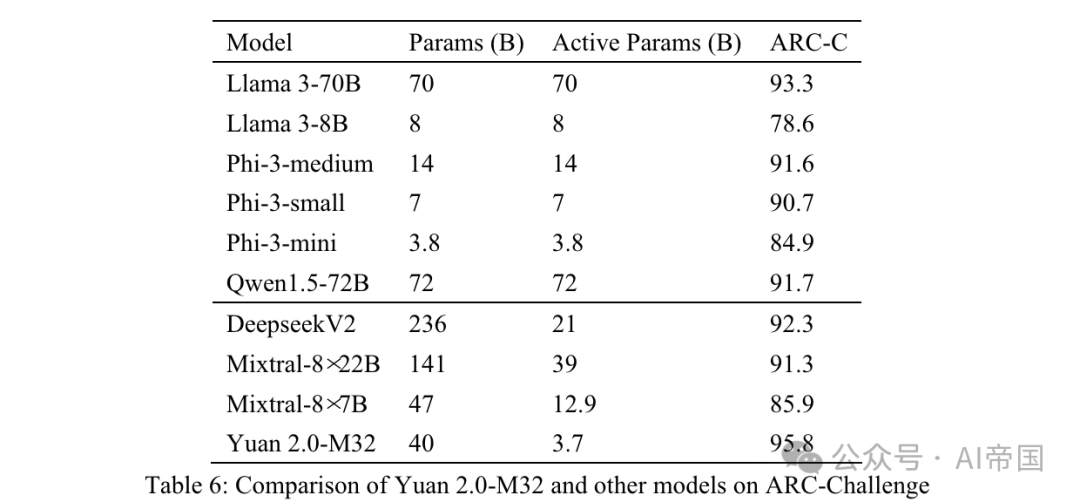Table 6: Comparison between Yuan 2.0-M32 and other models on ARC-Challenge

Questions and options are directly connected and used Separate. The previous text is sent to the model, which is expected to generate a label or corresponding answer. The generated answers are compared with the real answers and the results are calculated using the MC1 target.

Table 6 shows the results for ARC-C showing that Yuan 2.0-M32 excels at solving complex scientific problems—it outperforms Llama3-70B on this benchmark.

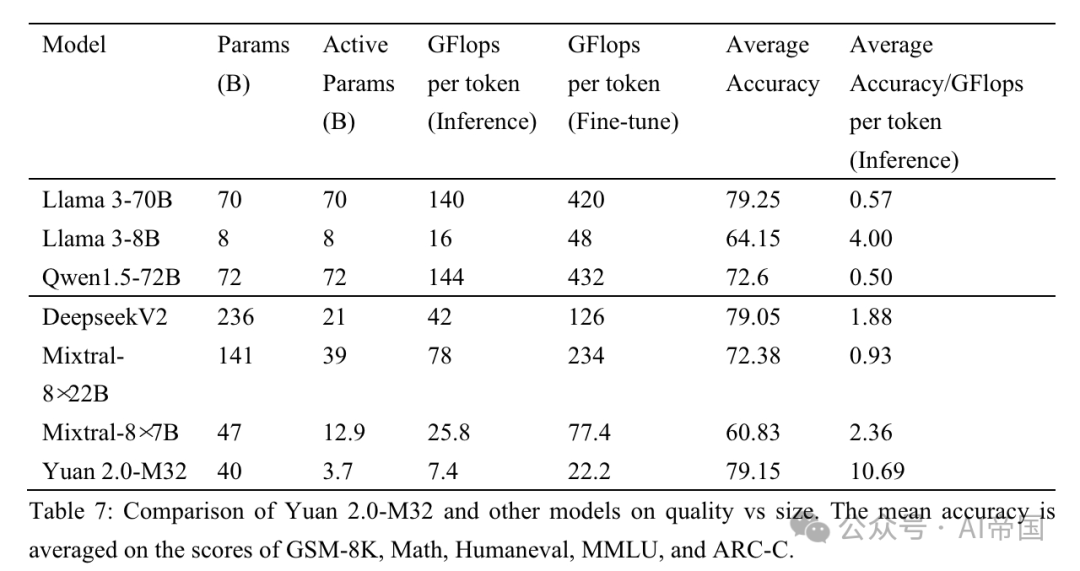Picture

Table 7: Quality and size comparison between Yuan 2.0-M32 and other models. Average accuracy is averaged from scores for GSM-8K, Math, Humaneval, MMLU and ARC-C

The paper compares the performance of the paper with three MoE models (Mixtral family, Deepseek) and six dense models (Qwen (Bai et al., 2023), Llama family, and Phi-3 family (Abdin et al., 2024)) A comparison is made to evaluate the performance of Yuan 2.0-M32 in different areas. Table 7 shows the comparison between accuracy and computational effort between Yuan 2.0-M32 and other models. Yuan 2.0-M32 is fine-tuned using only 3.7B active parameters and 22.2 GFlops per token, which is the most economical to obtain results that are comparable to or even surpass the other models listed in the table. Table 7 hints at the excellent computational efficiency and performance of the paper model during the inference process. The Yuan 2.0-M32 has an average accuracy of 79.15, which is comparable to the Llama3-70B. The average accuracy/GFlops per token value is 10.69, which is 18.9 times that of Llama3-70B.

Paper title: Yuan 2.0-M32: Mixture of Experts with Attention Router

Paper link: https://www.php.cn/link/cc7d159d6ff3ea6f39b9419877dfc81f

##

The above is the detailed content of LLM | Yuan 2.0-M32: Expert Mixture Model with Attention Routing. For more information, please follow other related articles on the PHP Chinese website!