Heim >Technologie-Peripheriegeräte >KI >Durch die Umwandlung mathematischer Probleme in Code hat die Forschung von Google die Genauigkeit maschineller Beweise erheblich verbessert.
Durch die Umwandlung mathematischer Probleme in Code hat die Forschung von Google die Genauigkeit maschineller Beweise erheblich verbessert.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-27 17:01:07952Durchsuche
Computer werden schon seit einiger Zeit zur Verifizierung mathematischer Beweise eingesetzt, allerdings können sie dies nur tun, wenn sie Probleme mit einer speziell entwickelten Beweissprache vorbereiten und nicht mit der von Mathematikern verwendeten Mischung aus mathematischer Notation und geschriebenem Text umgehen können.
Wenn Sie in natürlicher Sprache geschriebene mathematische Probleme in formale Codes umwandeln und sie für Computer leichter lösbar machen, kann dies dazu beitragen, Maschinen zu bauen, die neue Entdeckungen in der Mathematik erforschen können.
Dieser Prozess wird Formalisierung genannt, aber nur ein einziger Beweis kann jahrelange Arbeit erfordern, sodass nur ein kleiner Teil des mathematischen Wissens formalisiert und dann von Maschinen bewiesen wird.
Autoformalisierung bezieht sich auf die Aufgabe, Mathematik automatisch aus der natürlichen Sprache in die formale Sprache zu übersetzen. Die praktischen und philosophischen Implikationen eines erfolgreichen automatisierten Formalisierungstools wären enorm, es könnte die derzeit übermäßig hohen Formalisierungskosten reduzieren und auf lange Sicht könnte es automatisierte Aspekte des mathematischen Denkens in verschiedenen Forschungsbereichen verbinden.
In einer aktuellen Studie verwendeten Yuhuai Wu von Google und seine Mitarbeiter neuronale Netze von OpenAI Codex, um die Formalisierungsarbeit zu automatisieren. Codex wurde auf große Textmengen und Programmierdaten aus dem Web trainiert und Programmierer können damit zuverlässigen Code generieren. 🔜 Potenzial. Bisherige Erfolge beschränkten sich jedoch auf formale Sprachen (wie Python), für die im Web große Korpora existieren. Im Gegensatz dazu sind formale mathematische Daten sehr rar. Eine der größten formalen mathematischen Sprachbibliotheken, Archive of Formal Proofs, ist nur 180 MB groß, was weniger als 0,18 % der Trainingsdaten des großen Sprachmodells Codex ausmacht.
Darüber hinaus gibt es im Gegensatz zu allgemeinen Programmiersprachen, bei denen Docstrings in natürlicher Sprache weit verbreitet sind, kaum eine Datenangleichung zwischen natürlichen Sprachen und formalen mathematischen Sprachen. Daher ist noch nicht bekannt, ob der Erfolg groß angelegter Sprachmodelle die Entwicklung der automatischen Formalisierung direkt fördern kann. 
Um die Wirksamkeit dieses automatisierten Formalisierers zu testen, wandte das Team Codex dann auf eine Reihe von Problemen an, für die es bereits menschliche formalisierte Versionen gab, für die Codex auch eigene formalisierte Versionen generierte. Das Team nutzte eine andere KI namens MiniF2F, um beide Versionen des Problems zu lösen.
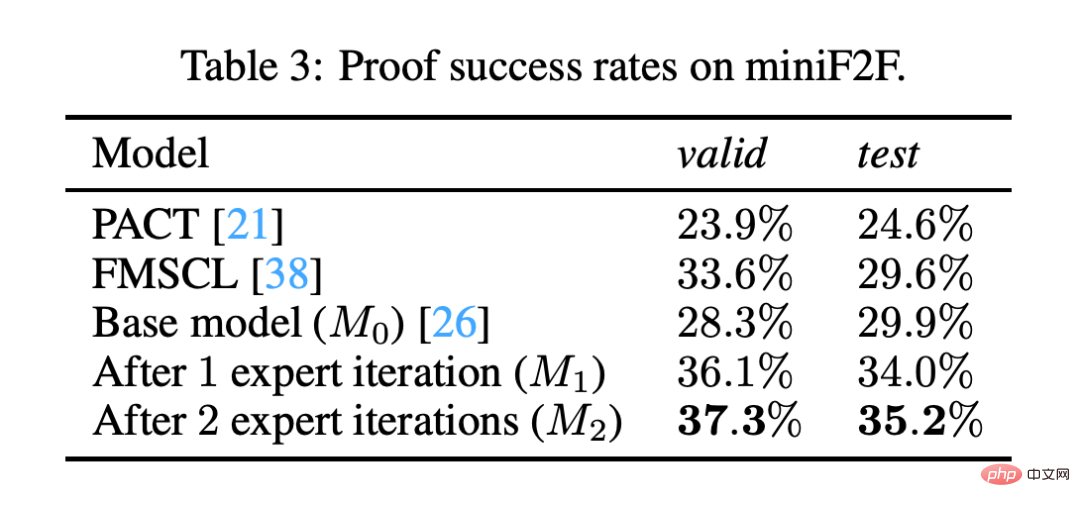
Die automatische Formalisierung des Problems erhöht die Erfolgsquote von MiniF2F von 29 % auf 35 %, was darauf hindeutet, dass Codex wichtige Fortschritte bei der Problemformalisierung gemacht hat.
 Es ist erwähnenswert, dass Aussagen in vielen Mathematikwettbewerben in der Regel so formuliert sind, dass man eher die Antwort auf eine bestimmte Frage finden soll als einen gegebenen Satz zu beweisen. Formale mathematische Aussagen haben jedoch die Form von Sätzen und nicht von Fragen.
Es ist erwähnenswert, dass Aussagen in vielen Mathematikwettbewerben in der Regel so formuliert sind, dass man eher die Antwort auf eine bestimmte Frage finden soll als einen gegebenen Satz zu beweisen. Formale mathematische Aussagen haben jedoch die Form von Sätzen und nicht von Fragen.
Um eine Frage in einen Vorschlag umzuwandeln, fügte der Forscher „Die endgültige Antwort“ nach der Frage hinzu:
 Das für die automatische Formalisierung verwendete Eingabeaufforderungsformat ist:
Das für die automatische Formalisierung verwendete Eingabeaufforderungsformat ist:
Wird KI mit menschlichen Mathematikern konkurrieren?
Das ist eine interessante Entwicklung, aber Wu sagte: Die Arbeit des Teams ist nur ein Proof of Concept. „Wenn das Ziel darin besteht, eine Maschine zu trainieren, die mit den besten menschlichen Mathematikern vergleichbar ist, dann scheint die automatische Formalisierung der Schlüsselweg zu sein, um dieses Ziel zu erreichen.“ Die Erfolgsquote wird weiter verbessert, die KI wird in der Lage sein, mit menschlichen Mathematikern zu konkurrieren. „
Wenn wir 100 % erreichen, werden wir definitiv einen KI-Agenten entwickeln, der die Goldmedaille der Internationalen Mathematikolympiade gewinnt.“Das unmittelbare Ziel des Teams besteht darin, automatische formale Modelle und automatisierte Beweismaschinen zu verbessern, aber die Zukunft der Forschungsergebnisse Die Auswirkungen werden weitreichend sein. Laut Wu können diese Modelle Bereiche der Mathematik aufdecken, die dem Menschen derzeit unbekannt sind.
Die Argumentationsfähigkeiten dieser Maschine eignen sich auch sehr gut für Verifizierungsaufgaben in einem breiteren Spektrum von Bereichen. „Sie können überprüfen, ob eine Software genau das tut, was Sie wollen, oder Sie können einen Hardware-Chip überprüfen, sodass er sowohl in Finanzhandelsalgorithmen als auch im Hardware-Design Anwendung findet.
Der Einsatz von Maschinen zur Erforschung der Mathematik ist spannend.“ Entwicklung, aber die eigentliche Herausforderung besteht darin, das Modell in der mathematischen Forschung zu verwenden, die größtenteils in LaTex geschrieben ist, sagt Yang-Hui He vom Institute of Mathematical Sciences in London. „Wir verwenden LaTex nur, weil es reibungslos zu tippen ist, aber es ist in gewisser Weise eine natürliche Sprache und hat seine eigenen Regeln
Er sagte, weil Benutzer ihre eigenen Funktionen und Symbole in LaTeX definieren können, diese Funktionen und Symbole.“ darf nur in einer Mathematikarbeit verwendet werden, was für neuronale Netze, die nur auf Klartext trainiert werden, schwierig sein kann.
Das obige ist der detaillierte Inhalt vonDurch die Umwandlung mathematischer Probleme in Code hat die Forschung von Google die Genauigkeit maschineller Beweise erheblich verbessert.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

