10 Codezeilen zur Vervollständigung des Diagrammtransformators, des DGL-Graphen-Neuronalnetzwerk-Frameworks, das Version 1.0 einleitet

Im Jahr 2019 haben die New York University und Amazon Cloud Technology gemeinsam das Graph-Neuronale-Netzwerk-Framework DGL (Deep Graph Library) auf den Markt gebracht. Jetzt ist DGL 1.0 offiziell veröffentlicht! DGL 1.0 fasst die verschiedenen Anforderungen an Graph Deep Learning und Graph Neural Network (GNN)-Technologie in Wissenschaft und Industrie in den letzten drei Jahren zusammen. Von der akademischen Forschung an hochmodernen Modellen bis hin zur Skalierung von GNNs für industrielle Anwendungen bietet DGL 1.0 eine umfassende und benutzerfreundliche Lösung für alle Benutzer, um die Vorteile des maschinellen Lernens mit Graphen besser zu nutzen.

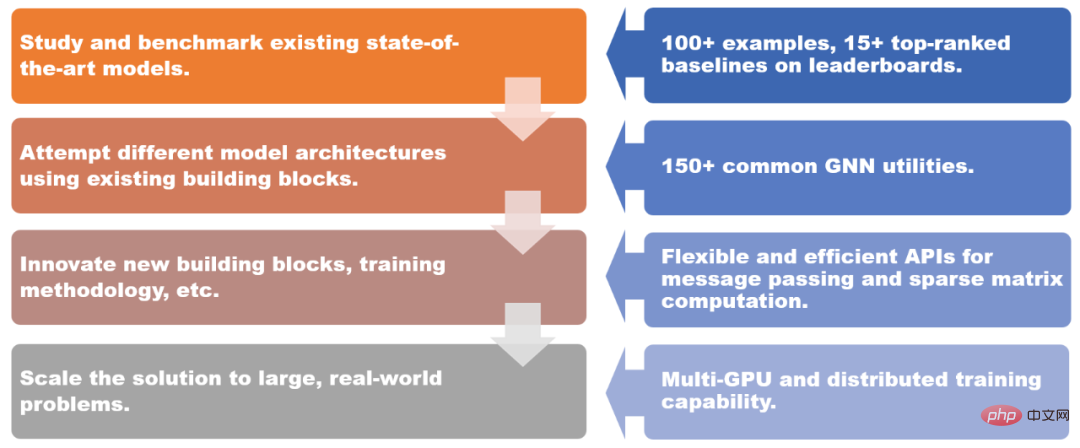
DGL 1.0 bietet Lösungen für verschiedene Szenarien.

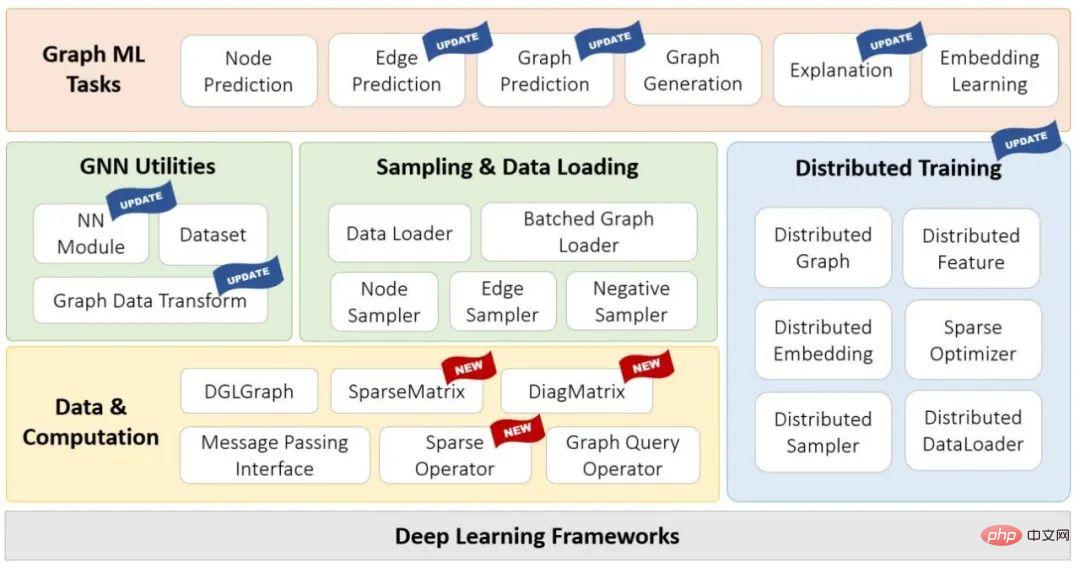
DGL 1.0 verfügt über ein mehrschichtiges und modulares Design, um verschiedenen Benutzeranforderungen gerecht zu werden. Zu den Hauptmerkmalen dieser Version gehören:

• 100+ sofort einsatzbereite GNN-Modellbeispiele, 15+ erstklassige Benchmark-Modelle im Open Graph Benchmark (OGB);
• 150+ gängige GNN-Module, einschließlich GNN Ebenen, Datensätze, Diagrammdatenkonvertierungsmodule, Diagrammsampler usw. können zum Erstellen neuer Modellarchitekturen oder GNN-basierter Lösungen verwendet werden GNN-Module;
• Multi-GPU- und verteilte Trainingsfunktionen unterstützen das Training auf zig Milliarden Graphen.

DGL 1.0 Technologie-Stack-Diagramm

Adresse: https://github.com/dmlc/dgl

Einer der Höhepunkte dieser Version ist die Einführung von DGL-Sparse, einer neuen Programmierschnittstelle, die spärliche Matrizen als Kernprogrammierungsabstraktion verwendet. DGL-Sparse vereinfacht nicht nur die Entwicklung vorhandener GNN-Modelle wie Graph-Faltungsnetzwerke, sondern funktioniert auch mit den neuesten Modellen, einschließlich diffusionsbasierter GNNs, neuronalen Hypergraph-Netzwerken und Graph-Transformatoren.

Die Veröffentlichung der DGL-Version 1.0 hat im Internet begeisterte Reaktionen hervorgerufen. Gelehrte wie Yann Lecun, einer der drei Giganten des Deep Learning, und Xavier Bresson, außerordentlicher Professor an der National University of Singapore, haben alle geliked und habe es weitergeleitet.

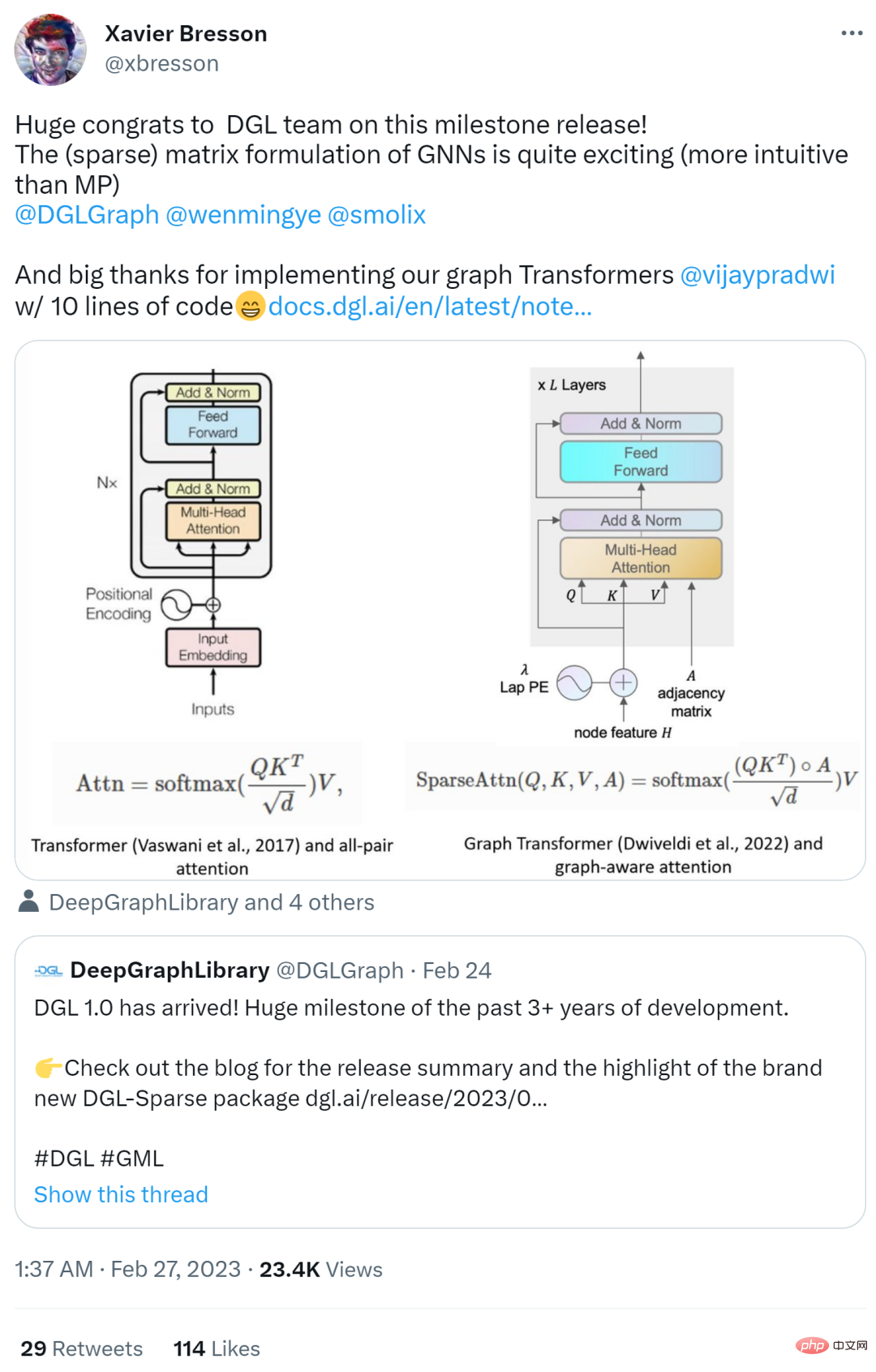
Im folgenden Artikel skizziert der Autor zwei gängige GNN-Paradigmen, nämlich die Message-Passing-Ansicht und die Matrix-Ansicht. Diese Paradigmen können Forschern helfen, den inneren Arbeitsmechanismus von GNN besser zu verstehen, und die Matrixperspektive ist auch eine der Motivationen für die Entwicklung von DGL Sparse.

Message Passing View und Matrix View

Im Film „Arrival“ gibt es ein Sprichwort: „Die Sprache, die Sie verwenden, bestimmt Ihre Denkweise und beeinflusst Ihre Sicht auf die Dinge.“ Dieser Satz ist auch für GNN geeignet.

bedeutet, dass graphische neuronale Netze zwei unterschiedliche Paradigmen haben. Die erste, sogenannte Message-Passing-Ansicht, drückt das GNN-Modell aus einer feinkörnigen, lokalen Perspektive aus und beschreibt detailliert, wie Nachrichten entlang von Kanten ausgetauscht werden und wie Knotenzustände entsprechend aktualisiert werden. Die zweite ist die Matrixperspektive. Da Graphen eine algebraische Äquivalenz mit dünn besetzten Adjazenzmatrizen aufweisen, entscheiden sich viele Forscher dafür, GNN-Modelle aus einer grobkörnigen, globalen Perspektive auszudrücken, wobei der Schwerpunkt auf Operationen mit dünn besetzten Adjazenzmatrizen und Eigenvektoren liegt.

Die Message-Passing-Perspektive zeigt den Zusammenhang zwischen GNNs und dem Graphisomorphismustest von Weisfeiler Lehman (WL), der auch auf der Aggregation von Informationen von Nachbarn beruht. Die Matrixperspektive versteht GNN aus einer algebraischen Perspektive, was zu einigen interessanten Entdeckungen führt, wie zum Beispiel dem Überglättungsproblem.

Kurz gesagt, diese beiden Perspektiven sind unverzichtbare Werkzeuge für die Untersuchung von GNN. Sie ergänzen sich und helfen Forschern, die Natur und Eigenschaften von GNN-Modellen besser zu verstehen und zu beschreiben. Aus diesem Grund besteht eine der Hauptmotivationen für die Veröffentlichung von DGL 1.0 darin, Unterstützung für die Matrixperspektive basierend auf der vorhandenen Message-Passing-Schnittstelle hinzuzufügen.

DGL Sparse: eine Sparse-Matrix-Bibliothek, die für das maschinelle Lernen von Graphen entwickelt wurde

DGL 1.0 Version verfügt über eine neue Bibliothek namens DGL Sparse (dgl.sparse), die zusammen mit der Message-Passing-Schnittstelle in DGL eine verbesserte Unterstützung für bietet alle Arten von graphischen neuronalen Netzwerkmodellen. DGL Sparse bietet Sparse-Matrix-Klassen und -Operationen speziell für das maschinelle Lernen von Graphen und erleichtert so das Schreiben von GNNs aus einer Matrixperspektive. Im nächsten Abschnitt demonstrieren die Autoren mehrere GNN-Beispiele und zeigen ihre mathematischen Formulierungen und entsprechenden Codeimplementierungen in DGL Sparse.

Graph Convolutional Network

GCN ist einer der Pioniere der GNN-Modellierung. GCN kann sowohl mit der Message-Passing-Ansicht als auch mit der Matrixansicht dargestellt werden. Der folgende Code vergleicht die Unterschiede zwischen diesen beiden Methoden in DGL.

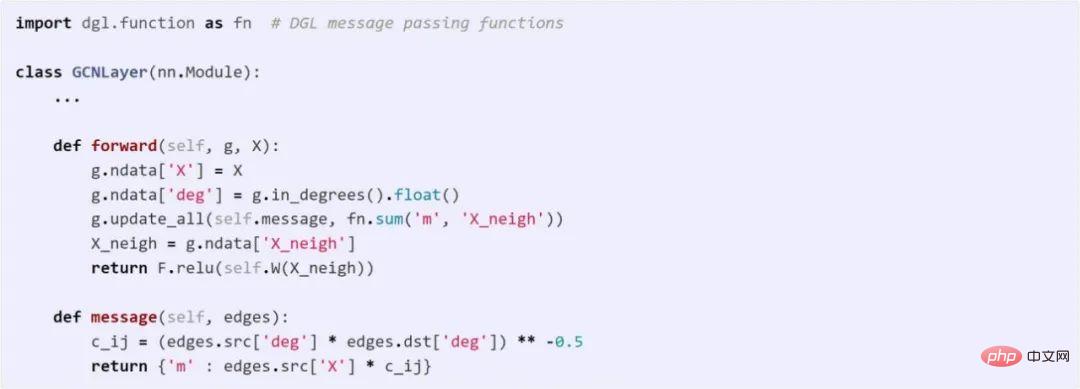
Verwenden Sie die Messaging-API zur Implementierung

Verwendung von DGL Sparse zur Implementierung von GCN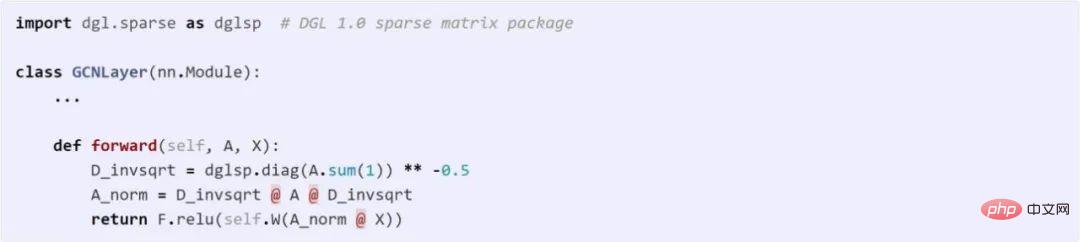

GNN basierend auf Graphdiffusion

Graphdiffusion ist der Prozess der Ausbreitung oder Glättung von Knotenmerkmalen oder Signalen entlang von Kanten. Viele klassische Diagrammalgorithmen wie PageRank fallen in diese Kategorie. Eine Reihe von Studien hat gezeigt, dass die Kombination von Graphdiffusion mit neuronalen Netzen eine effektive und effiziente Möglichkeit ist, Modellvorhersagen zu verbessern. Die folgende Gleichung beschreibt die Kernberechnung eines der repräsentativeren Modelle, APPNP. Es kann direkt in DGL Sparse implementiert werden.

Hypergraph Neural Network

Ein Hypergraph ist eine Verallgemeinerung von Graphen, bei der Kanten eine beliebige Anzahl von Knoten verbinden können (sogenannte Hyperkanten). Hypergraphen sind besonders nützlich in Szenarien, in denen Beziehungen höherer Ordnung erfasst werden müssen, wie etwa Co-Kaufverhalten auf E-Commerce-Plattformen oder Co-Autorenschaft in Zitiernetzwerken. Ein typisches Merkmal eines Hypergraphen ist seine spärliche Korrelationsmatrix, daher werden neuronale Hypergraphennetze (HGNN) häufig mithilfe spärlicher Matrizen definiert. Das Folgende ist ein Hypergraph-Faltungsnetzwerk (Feng et al., 2018) und seine Code-Implementierung. Das Transformer-Modell hat sich zur erfolgreichsten Modellarchitektur in der Verarbeitung natürlicher Sprache entwickelt. Forscher beginnen auch, Transformer auf das maschinelle Lernen mit grafischen Darstellungen auszudehnen. Dwivedi et al. waren Vorreiter bei der Idee, die gesamte Multi-Head-Aufmerksamkeit auf verbundene Knotenpaare im Diagramm zu beschränken. Dieses Modell kann mit dem DGL Sparse-Tool einfach mit nur 10 Codezeilen implementiert werden.

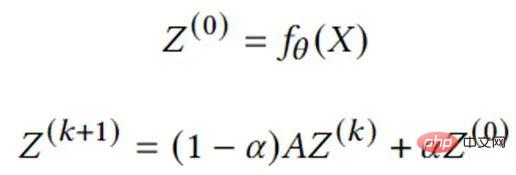
Hauptmerkmale von DGL Sparse Die folgenden Hauptfunktionen:

Automatische Auswahl des Sparse-Formats

: DGL Sparse ist so konzipiert, dass Benutzer sich keine Gedanken über die Auswahl der richtigen Datenstruktur zum Speichern von Sparse-Matrizen (auch als Sparse-Formate bezeichnet) machen müssen ). Benutzer müssen sich nur daran erinnern, dass dgl.sparse.spmatrix eine spärliche Matrix erstellt und DGL intern automatisch das optimale Format basierend auf dem aufgerufenen Operator

Skalar- oder Vektor-Nicht-Null-Elemente

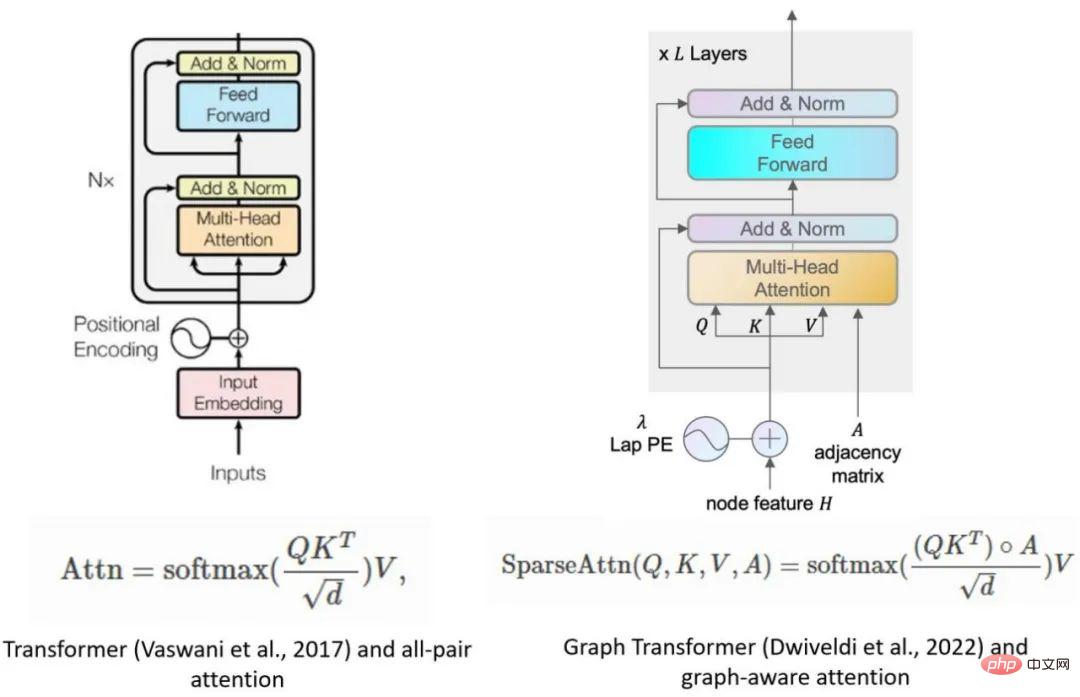
• auswählt: a Viele GNN-Modelle lernen mehrere Gewichte an den Kanten (z. B. die Mehrkopf-Aufmerksamkeitsvektoren, die im Beispiel des Graph Transformer gezeigt werden). Um dieser Situation gerecht zu werden, ermöglicht DGL Sparse, dass Nicht-Null-Elemente Vektorformen haben und gängige Sparse-Operationen wie die Sparse-Dense-Matrix-Multiplikation (SpMM) usw. erweitert werden. Sie können sich auf die bspmm-Operation im Graph Transformer-Beispiel beziehen. Durch die Nutzung dieser Designmerkmale reduziert DGL Sparse die Codelänge um durchschnittlich das 2,7-fache
• im Vergleich zu früheren Implementierungen von Matrixansichtsmodellen, die Nachrichtenübermittlungsschnittstellen verwenden. Der vereinfachte Code reduziert außerdem den Framework-Overhead um 43 %. Darüber hinaus ist DGL Sparse mit PyTorch kompatibel und lässt sich problemlos in verschiedene Tools und Pakete im PyTorch-Ökosystem integrieren. Erste Schritte mit DGL 1.0

DGL 1.0 wurde auf allen Plattformen veröffentlicht und kann einfach mit Pip oder Conda installiert werden. Zusätzlich zu den zuvor vorgestellten Beispielen enthält die erste Version von DGL Sparse auch 5 Tutorials und 11 End-to-End-Beispiele, die alle direkt in Google Colab erlebt werden können, ohne dass eine lokale Installation erforderlich ist.

Weitere Informationen zu den neuen Funktionen von DGL 1.0 finden Sie im Veröffentlichungsprotokoll des Autors. Wenn Sie bei der Verwendung von DGL auf Probleme stoßen oder Vorschläge oder Feedback haben, können Sie das DGL-Team auch über das Diskussionsforum oder Slack kontaktieren.

Das obige ist der detaillierte Inhalt von10 Codezeilen zur Vervollständigung des Diagrammtransformators, des DGL-Graphen-Neuronalnetzwerk-Frameworks, das Version 1.0 einleitet. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!