九种聚类算法，探索无监督机器学习

今天，我想和大家分享一下机器学习中常见的无监督学习聚类方法

在无监督学习中，我们的数据并不带有任何标签，因此在无监督学习中要做的就是将这一系列无标签的数据输入到算法中，然后让算法找到一些隐含在数据中的结构，通过下图中的数据，可以找到的一个结构就是数据集中的点可以分成两组分开的点集（簇），能够圈出这些簇（cluster）的算法，就叫做聚类算法（clustering algorithm）。

聚类算法的应用

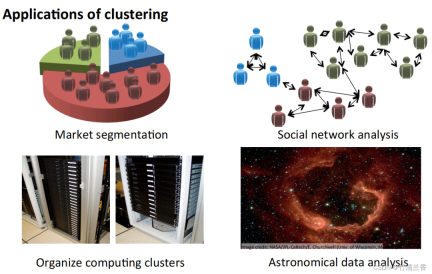
• 市场分割：将数据库中客户的信息根据市场进行不同的分组，从而实现对其分别销售或者根据不同的市场进行服务改进。
• 社交网络分析：通过邮件最频繁联系的人及其最频繁联系的人来找到一个关系密切的群体。
• 组织计算机集群：在数据中心里，计算机集群经常一起协同工作，可以用它来重新组织资源、重新布局网络、优化数据中心以及通信数据。
• 了解银河系的构成：利用这些信息来了解一些天文学的知识。

聚类分析的目标是将观测值划分为组（“簇”），以便分配到同一簇的观测值之间的成对差异往往小于不同簇中的观测值之间的差异。聚类算法分为三种不同的类型：组合算法、混合建模和模式搜索。

常见的几种聚类算法有：

• K-Means Clustering
• Hierarchical Clustering
• Agglomerative Clustering
• Affinity Propagation
• Mean Shift Clustering
• Bisecting K-Means
• DBSCAN
• OPTICS
• BIRCH

K-means

K-means 算法是目前最流行的聚类方法之一。

K-means 是由贝尔实验室的 Stuart Lloyd 在 1957 年提出来的，最开始是用于脉冲编码调制，直到 1982 年才将该算法对外公布。1965 年，Edward W.Forgy 发布了相同的算法，因此 K-Means 有时被称为 Lloyd-Forgy。

聚类问题通常需要处理一组未经标记的数据集，并且需要一个算法来自动将这些数据分成有紧密关系的子集或簇。目前，最流行和广泛应用的聚类算法是K均值算法

直观理解 K 均值算法：

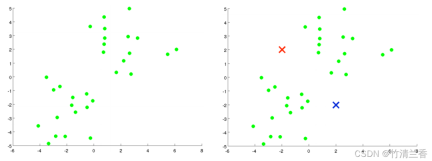
假如有一个无标签的数据集（上图左），并且我们想要将其分为两个簇，现在执行 K 均值算法，具体操作如下：

• 第一步，随机生成两个点（因为想要将数据聚成两类）（上图右），这两个点叫做聚类中心（cluster centroids）。
• 第二步，进行 K 均值算法的内循环。K 均值算法是一个迭代算法，它会做两件事情，第一个是簇分配（cluster assignment），第二个是移动聚类中心（move centroid）。

内循环的第一步是要进行簇分配，也就是说，遍历每一个样本，再根据每一个点到聚类中心距离的远近将其分配给不同的聚类中心（离谁近分配给谁），对于本例而言，就是遍历数据集，将每个点染成红色或蓝色。

内循环的第二步是将聚类中心移动，使得红色和蓝色的聚类中心分别移动到它们所属点的平均位置

将所有的点根据与新的聚类中心距离的远近进行新的簇分配，并且不断循环此过程，直到聚类中心的位置不再随着迭代而改变，同时点的颜色也不再发生改变。这时可以说K均值已经完成了聚合。这个算法在找出数据中的两个簇方面表现相当出色

K-Means算法的优点：

简单易懂，计算速度较快，适用于大规模数据集。

缺点：

• 例如对于非球形簇的处理能力较差，容易受到初始簇心的选择影响，需要预先指定簇的数量K等。
• 此外，当数据点之间存在噪声或者离群点时，K-Means算法可能会将它们分配到错误的簇中。

Hierarchical Clustering

层次聚类是按照某个层次对样本集进行聚类的操作。这里的层次指的实际上是某种距离的定义

聚类的最终目的是减少分类的数量，因此在行为上类似于从叶子节点向根节点逐步靠近的树状图过程，这种行为也被称为“自下而上”

更通俗的，层次聚类是将初始化的多个类簇看做树节点，每一步迭代，都是将两两相近的类簇合并成一个新的大类簇，如此反复，直至最终只剩一个类簇（根节点）。

层次聚类策略分为两种基本范式：聚集型(自下而上)和分裂型(自上而下)。

与层次聚类相反的是分裂聚类，也称为DIANA(Divise Analysis)，其行为过程为“自上而下”

K-means算法的结果取决于选择搜索的聚类数量和起始配置的分配。而相反，层次聚类方法则不需要这样的规范。相反，它们要求用户根据两组观察值之间的成对差异性来指定（不相交）观察组之间的差异性度量。顾名思义，层次聚类方法产生一个层次结构表示，其中每个层次的集群都是通过合并下一个较低级别的集群而创建的。在最低级别，每个集群包含一个观察值。在最高级别，只有一个集群包含所有的数据

优点：

• 距离和规则的相似度容易定义，限制少；
• 不需要预先制定聚类数；
• 可以发现类的层次关系；
• 可以聚类成其它形状。

缺点：

• 计算复杂度太高；
• 奇异值也能产生很大影响；
• 算法很可能聚类成链状。

Agglomerative Clustering

重写后的内容为：凝聚层次聚类（Agglomerative Clustering）是一种自底向上的聚类算法，它将每个数据点看作一个初始簇，并逐步合并它们以形成更大的簇，直到满足停止条件。在该算法中，每个数据点最初被视为一个单独的簇，然后逐步合并簇，直到所有数据点合并为一个大簇

优点：

• 适用于不同形状和大小的簇，且不需要事先指定聚类数目。
• 该算法也可以输出聚类层次结构，便于分析和可视化。

缺点：

• 计算复杂度较高，尤其是在处理大规模数据集时，需要消耗大量的计算资源和存储空间。
• 该算法对初始簇的选择也比较敏感，可能会导致不同的聚类结果。

Affinity Propagation

修改后的内容：亲和传播算法（AP）通常被翻译为亲和力传播算法或者邻近传播算法

Affinity Propagation 是一种基于图论的聚类算法，旨在识别数据中的"exemplars"(代表点)和"clusters"(簇)。与 K-Means 等传统聚类算法不同，Affinity Propagation 不需要事先指定聚类数目，也不需要随机初始化簇心，而是通过计算数据点之间的相似性得出最终的聚类结果。

优点：

• 不需要制定最终聚类族的个数
• 已有的数据点作为最终的聚类中心，而不是新生成一个簇中心。
• 模型对数据的初始值不敏感。
• 对初始相似度矩阵数据的对称性没有要求。
• 相比与 k-centers 聚类方法，其结果的平方差误差较小。

缺点：

• 该算法的计算复杂度较高，需要大量的存储空间和计算资源；
• 对于噪声点和离群点的处理能力较弱。

Mean Shift Clustering

平移聚类是一种基于密度的非参数聚类算法，其基本思想是通过寻找数据点密度最大的位置（称为“局部最大值”或“高峰”），来识别数据中的群集。该算法的核心在于对每个数据点进行局部密度估计，并将密度估计结果用于计算数据点移动的方向和距离

优点：

• 不需要指定簇的数目，且对于形状复杂的簇也有很好的效果。
• 算法还能够有效地处理噪声数据。

缺点：

• 计算复杂度较高，尤其是在处理大规模数据集时，需要消耗大量的计算资源和存储空间；
• 该算法还对初始参数的选择比较敏感，需要进行参数调整和优化。

Bisecting K-Means

Bisecting K-Means 是一种基于 K-Means 算法的层次聚类算法，其基本思想是将所有数据点划分为一个簇，然后将该簇分成两个子簇，并对每个子簇分别应用 K-Means 算法，重复执行这个过程，直到达到预定的聚类数目为止。

算法首先将所有数据点视为一个初始簇，然后对该簇应用K-Means算法，将该簇分成两个子簇，并计算每个子簇的误差平方和（SSE）。然后，选择误差平方和最大的子簇，并将其再次分成两个子簇，重复执行这个过程，直到达到预定的聚类数目为止。

优点：

• 具有较高的准确性和稳定性，能够有效地处理大规模数据集，并且不需要指定初始聚类数目。
• 该算法还能够输出聚类层次结构，便于分析和可视化。

缺点：

• 计算复杂度较高，尤其是在处理大规模数据集时，需要消耗大量的计算资源和存储空间。
• 此外该算法对初始簇的选择也比较敏感，可能会导致不同的聚类结果。

DBSCAN

基于密度的空间聚类算法DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种典型的具有噪声的聚类方法

密度的方法具有不依赖于距离的特点，而是依赖于密度。因此，它能够克服基于距离的算法只能发现“球形”聚簇的缺点

DBSCAN算法的核心思想是：对于一个给定的数据点，如果它的密度达到一定的阈值，则它属于一个簇中；否则，它被视为噪声点。

优点：

• 这类算法能克服基于距离的算法只能发现“类圆形”(凸)的聚类的缺点；
• 可发现任意形状的聚类，且对噪声数据不敏感；
• 不需要指定类的数目 cluster；
• 算法中只有两个参数，扫描半径 (eps)和最小包含点数(min_samples)。

缺点：

• 计算复杂度，不进行任何优化时，算法的时间复杂度是O(N^{2})，通常可利用R-tree，k-d tree, ball；
• tree索引来加速计算，将算法的时间复杂度降为O(Nlog(N))；
• 受eps影响较大。在类中的数据分布密度不均匀时，eps较小时，密度小的cluster会被划分成多个性质相似的cluster；eps较大时，会使得距离较近且密度较大的cluster被合并成一个cluster。在高维数据时，因为维数灾难问题，eps的选取比较困难；
• 依赖距离公式的选取，由于维度灾害，距离的度量标准不重要；
• 不适合数据集集中密度差异很大的，因为eps和metric选取很困难。

OPTICS

OPTICS（Ordering Points To Identify the Clustering Structure）是一种基于密度的聚类算法，它能够自动确定簇的数量，同时也能够发现任意形状的簇，并且能够处理噪声数据

OPTICS 算法的核心思想是根据给定数据点计算其与其他点之间的距离，以确定其在密度上的可达性，并构建一个基于密度的距离图。然后，通过扫描该距离图，自动确定簇的数量，并对每个簇进行划分

优点：

• 能够自动确定簇的数量，并能够处理任意形状的簇，并能够有效地处理噪声数据。
• 该算法还能够输出聚类层次结构，便于分析和可视化。

缺点：

• 计算复杂度较高，尤其是在处理大规模数据集时，需要消耗大量的计算资源和存储空间。
• 该算法对于密度差异较大的数据集，可能会导致聚类效果不佳。

BIRCH

BIRCH（平衡迭代降低和层次聚类）是一种基于层次聚类的聚类算法，它能够高效地处理大规模数据集，并且对于任何形状的簇都能够取得良好的效果

BIRCH算法的核心思想是：透過對數據集進行分層聚類，逐步減小數據規模，最終得到簇結構。BIRCH算法採用一種類似於B樹的結構，稱為CF樹，它可以快速地插入和刪除子簇，並且可以自動平衡，從而確保簇的質量和效率

优点：

• 能够快速处理大规模数据集，并且对于任意形状的簇都有较好的效果。
• 该算法对于噪声数据和离群点也有较好的容错性。

缺点：

• 对于密度差异较大的数据集，可能会导致聚类效果不佳；
• 对于高维数据集的效果也不如其他算法。

以上是九种聚类算法，探索无监督机器学习的详细内容。更多信息请关注PHP中文网其他相关文章！