
一、为何在意因果关系
首先介绍一下何为因果关系:
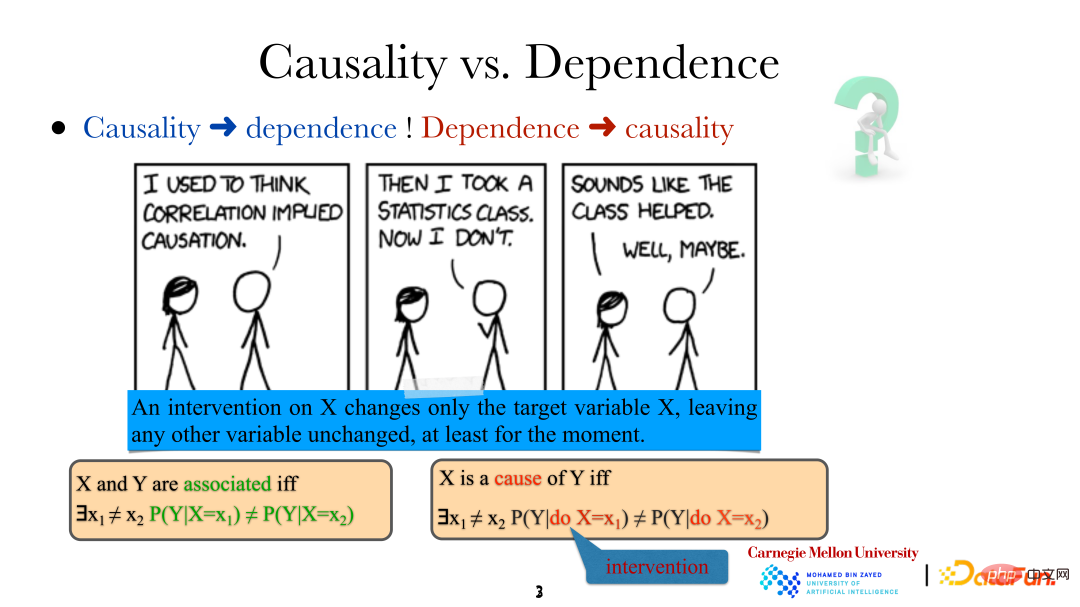
当我们说变量/事件之间是有关系的,意思是说它们不是独立的,这样它们之间一定存在一些关系。然而 X 是 Y 的“因”的含义是,如果采用特定方法改变 X(天下雨),Y(地面变湿)则会随之改变,即对 X 进行 “intervention” 人为干预时,Y 的分布是不一样的。需要注意的是,这里的干预不是随意的,而是非常精确的对目标变量(target variable)的直接控制(直接对“天下雨”进行改变),这个改变不会直接影响系统中的其他变量。同时通过这种方式,即直接人为干预,我们也能够确定某一变量是否是另一变量的直接原因。
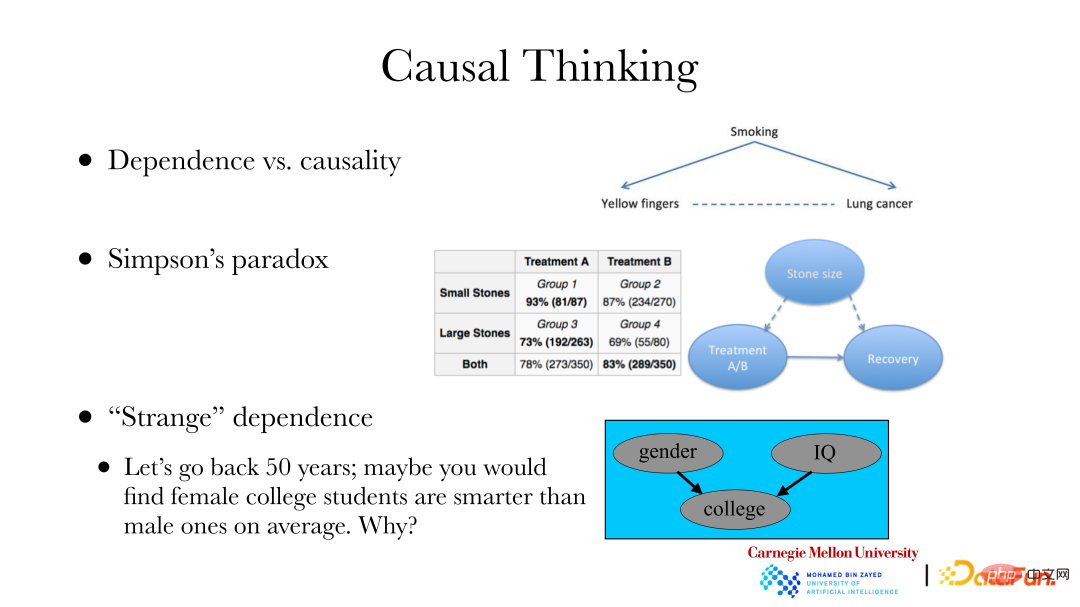
下面对分析因果关系的必要性进行了举例:
① 一个经典的案例是:肺病和指甲颜色通过抽烟存在着一些关系,即由于香烟没有过滤嘴,经常抽烟会使手指甲变黄,抽烟也可能导致肺部疾病。如果想改变某个地区肺部疾病的发病率,不能通过将指甲漂白来改善,需要找到导致肺部疾病的原因,而不是改变肺部疾病存在的依赖关系。要想达到改变肺部疾病发病率的目的,就需要进行因果分析。
② 第二个案例是:辛普森悖论。上图右边是一个真实的数据集,数据集展示了两组肾结石数据,一组结石比较小,另一组结石比较大;此外还有两种治疗方式 A 和 B。在表中可以发现,不管是小结石组还是大结石组,A 治疗方式获得的结果会好一些,治愈率分别是 93% 和 73%,B 治疗方式的治愈率分别是 87% 和 69%。但将同一治疗方法的两组结石病人混合在一起统计,整体来看 B 治疗方案的效果(83%)反而比 A(78%)更好。假设你是只在意治愈率的医生,对新病人该如何选择治疗方案。出现这种情况的原因在于,进行推荐时,我们只在意治疗方式到治愈的因果联系,而不在意其他依赖关系。然而石头大小是治疗方式和是否治愈的共同原因,它导致治疗方式和治愈的依赖关系在数量上发生改变。故当研究治疗方式和治愈的关系时,应该讨论前者对后者的因果关系,而不是依赖关系。
③ 第三个案例:在 50 年以前,统计显示高校中的女性平均会比男性更聪明,然而实际两者不应该有明显差异。这其中存在着选择偏差(selection bias),因为女性比男性更难进入大学,即学校招收学生时,会受到性别、考试能力等因素影响。当“果”已经发生时,性别和考试能力就会有某些关系了。当使用互联网采集的数据时也会存在选择偏差的问题。一个数据点是否被收集和某些属性往往是有关系的,如果仅分析被放置在互联网上的数据,就需要注意考虑这些因素。当意识到这一点时,也能通过因果关系来对有选择偏倚的数据进行分析,进而恢复或反推得到整个群体本身的性质。

上图展示了几个机器学习/深度学习的问题:
① 我们知道最有预测和数据的分布是有关系的。在迁移学习中,例如如果想要将一个模型从非洲迁移到美洲,还能进行最优预测,这显然就需要根据数据分布的不同对模型进行适应性调整。这时,分析数据的分布发生了什么变化,怎样发生变化就显得尤为重要。知道数据发生了什么变化,就能对模型进行相应的调整。另一个例子,当构建 AI 模型进行疾病诊断时,不会满足于机器提出的诊断结果,会进一步的想要知道机器为什么会得出这个结论,例如是哪一个 mutation(变异)导致了该疾病。此外,如何治疗疾病也会提出很多“为什么”的问题。同样,当推荐系统进行推荐时,会想知道为什么它会推荐该物品/策略,比如该公司仅仅想提高收益,或者该物品/策略很适合用户,又或者该物品/策略有益于未来。这些“为什么”的问题都是因果问题。
② 在深度学习领域中,存在着对抗攻击(adversarial attacks)的概念。如图,对左边的大熊猫图片加入一些特定噪声,或改变特定像素等,机器就将图片判定为其他类型动物,而不是大熊猫,并且其置信度还很高。然而对于人类来说,这两张图片明显都是大熊猫。这是因为目前机器从图片中学习到的高层特征和人类学习到的高层特征不吻合。如果机器使用的高层特征与人类不吻合,就有可能发生对抗攻击。在改变输入时,人类或机器的判断会发生改变,最终判定结果就会存在问题。只有让机器学习到与人类吻合的高层特征,即机器能按照人类的方式学习和使用特征,才能避免对抗攻击的情形。

为什么要进行因果表征?
① 使下游任务受益:如可以帮助下游的分类等任务做得更好。
② 能解释“为什么”这类问题。
③ 将数据背后真正的因果特征恢复出来:哲学中康德的形而上学认为,人类所感受到的世界是经验世界。它虽然基于背后的世界本体(world-in-itself), 但我们不能直接感知世界本体,经验世界中已经被感官系统自动添加了一些性质,如时间、空间、因果顺序等。由此,如果希望机器学习到与人类吻合的特征,就需要机器具有学习因果顺序/关系、时间、空间等特征的能力。
二、因果表征学习:独立同分布情形
1、因果表征学习基本概念
如何在独立同分布的情形下学习因果关系?首先需要回答两个问题:一是数据中有哪些性质是与因果关系有关的,在数据中有什么线索(“footprint”)。二是在获得数据的条件下,是否能恢复出其中的因果关系,即因果系统的可识别性问题。

因果系统最本质的性质是 “modularity”(模块性):虽然系统中的变量都存在一定的关系,但是可以从因果关系将系统划分成多个子系统(一个原因产生一个因变量)。例如,“天下雨”、“地面湿”、“地面滑”是相互依赖的,通过因果关系可以将其分别划分为三个子系统:“某些原因导致天下雨”,“天下雨导致地面湿”,“地面湿导致地上滑”。虽然变量间是有依赖关系的,但这三个 process(过程,即子系统)是没有联系的,不存在参数共享,改变一个系统不会导致另一系统的改变。如通过喷洒某些物质使“地面湿导致地上滑”的影响得到改变,这不会影响天是否下雨,也不会改变天下雨对地面湿的影响。这种性质就称为 “modularity”,即从因果的角度将系统划分为不同的子模块,且各个子模块间没有联系。
从模块性出发,可以得到因果系统的三个性质:
① 变量之间的条件独立性。
② 独立噪声条件。
③ 最小(和独立)变化。
关于因果系统的可识别性,一般来说机器学习本身不是非常关注可识别性问题的,例如预测模型需要判断预测结果是否准确或最优,但并没有一个“真相”进行判断。但因果分析/因果表征学习是为了恢复数据“真相”,即更关注是否能将数据背后的因果性质辨识出来。
下面介绍两个基本概念:
① 因果发现(causal discovery):通过数据探索背后的因果结构/模型。
② 因果表征学习(causal representation learning):从直接观察的数据中寻找背后高层的隐变量及变量间关系。
2、因果表征学习划分
因果表征学习方法一般从以下三个角度进行划分:
① 数据性质:是否独立同分布(“i.i.d. data”)。其中不独立同分布数据包括不独立但同分布数据,如存在时间依赖关系的同分布数据(如时间序列数据),也可以是独立但不同分布的数据,如数据分布发生了变化(或者这两者的结合)。
② 参数约束(“parameter constraints”):因果关系的影响上是否有其他额外性质,如参数模型。
③ 潜在混杂因素(“latent confounders”):是否允许系统中存在没有观察到的共同因子或者混淆因子。
下图详细展示了不同情形(setting)下能得到的具体结果:

如在独立同分布情形下,如果没有参数模型约束,不管是否有潜在混在因素,一般都能得到等价类(“equivalence class”),如果有参数模型约束,一般则能直接恢复背后的真相。
3、独立同分布因果表征学习

上图展示了在独立同分布情形下,没有参数模型约束的例子。数据一共展示了 250 个头骨的 8 个测量变量,包括性别、地点、天气,及头骨的大小、形状等。考古学家想知道造成不同地区的人外貌不同的原因是什么,如果知道这一因果关系,或许可以通过环境和其他因素的改变对人的外貌进行预测。显然在这种条件无法进行人为干预,即使加入了干预,也需要相当长的时间才能观测到结果,故只能从现有观测数据中寻找因果关系。
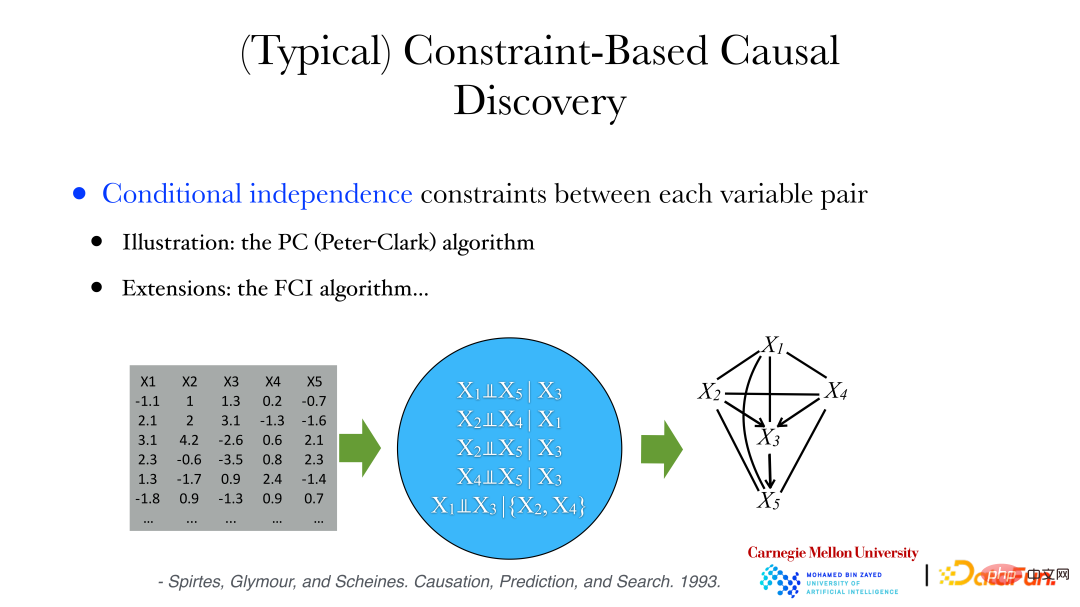
如上图所示,变量间关系是非常复杂的,可能是线性也可能是非线性,且变量维度也可能不一致。如性别是 1 维,头骨性状可能是 255 维。此时可以使用条件独立的性质来构建因果关系。
方法包括以下两种:
① PC(Peter-Clark)算法:算法假设系统中没有观察到共同因子。
② FCI 算法:用于有隐变量的情况。
下面将使用 PC 算法来分析考古学数据:从数据中可以得出一系列条件独立的性质,如变量 X1 和 X5 在给出 X3 时是条件独立等。同时我们可以证明,如果两变量是条件独立的,那它们之间是没有边的。然后,我们可以从完整的图出发,如果变量间是条件独立的,则去掉相连的边,即可得到无向图,然后对图中边的方向进行判断,就可以找出有向无环图(DAG,Directed Acyclic Graph)或者一些有向无环图的集合来满足数据中变量间的条件独立约束。
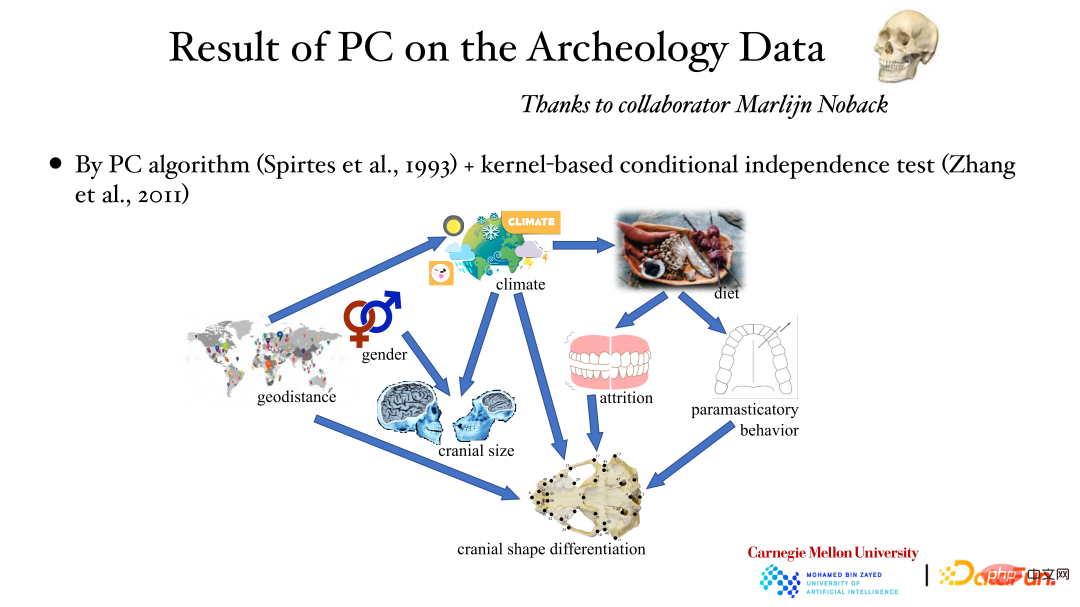
上图展示了使用 PC 算法和核条件独立检验方法对考古学数据进行分析的结果:地理位置影响天气,天气影响头骨大小,此外性别也会影响头骨大小等。通过数据分析得到了其背后的因果关系。
在刚才提到两个问题中,一个是需要找到变量 DAG 的每一条边的方向,这需要做额外的假设。如果将因对果如何发生影响做一些假设,会发现因和果是不对称的,这样就能找出因果方向。下图中的数据背景还是独立同分布数据,并添加了额外的参数限制,且依然不允许系统中存在混淆因子。这时可以使用以下三种类型模型来研究因果方向:
① 线性非高斯模型(Linear non-Gaussian model);
② 后-非线性因果模型(PNL,Post-nonlinear causal model);
③ 加性噪声模型(ANM,Additive noise model)。
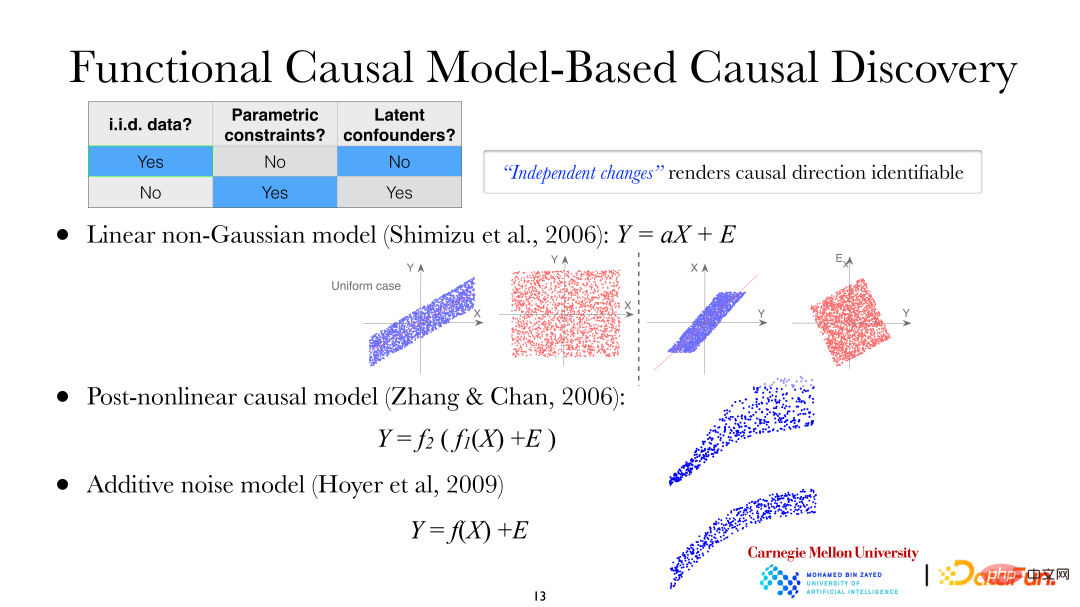
在线性非高斯模型中,假设从 X 导致 Y,即 X 为因变量,Y 为果变量。从图中可以看出,用 X 解释 Y 进行线性回归时,残差和 X 是独立的;但是反过来,使用 Y 来解释 X 进行线性回归时,残差和 Y 之间是不相关的,但很明显不是独立的(线性高斯情况下,变量间不相关表示独立。但此刻模型是线性非高斯,即不相关并不代表它们独立)。可以发现因变量和果变量之间是不对称的。这种情况同样适用于后-非线性因果模型和加性噪声模型。

上图展示了后-非线性因果模型:外面的第 2 个非线性函数(f2)一般用于描述系统中的测量过程中引入到非线性变化,在观察/测量数据时经常会存在非线性变化。如生物领域中,用仪器测量基因表达数据时会有额外的非线性变化。线性模型(Linear models)、非线性加性噪声模型(Nonlinear additive noise models)以及乘性噪声模型(Multiplicative noise models)等都是 PNL 模型的特例。
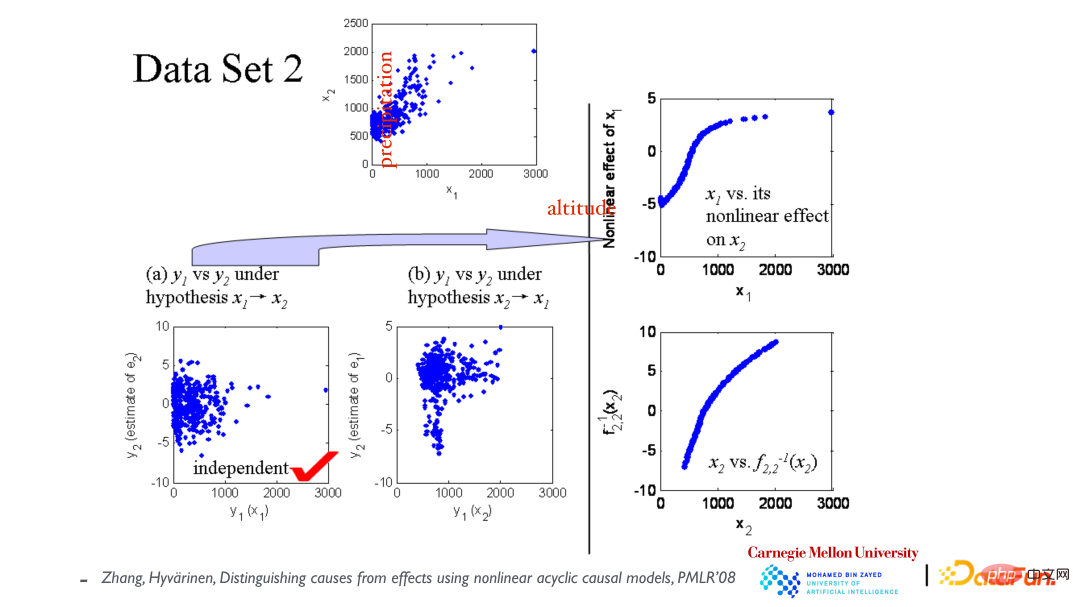
最上方的散点图展示了变量 x1(海拔高度)和 x2(年降雨量)的关系。首先假设 x1 导致了 x2,然后构建模型来拟合数据,如左下角图所示,残差和 x1 是独立的;然后假设 x2 导致了 x1,再次拟合模型,我们发现发现残差和 x2 不独立(见中间图片)。由此,得出因果方向是由 x1 导致 x2 的。

从上一个例子中确实可以找到因果变量的不对称性,但从理论上这个结果是否能被保证?且是唯一的正确结果,反方向(果到因)是无法解释数据的呢?证明如上表所示,五种情形下两个方向(因到果,果到因)都可以对数据进行解释,这五个都是非常特殊的情形。第一个是线性高斯模型,关系是线性的,分布是高斯的,这时因果的不对称性消失了。其他四个都是特殊模型。

即使数据是用后非线性模型进行分析的,因果都是能够被区分的,正确的方向能够找到独立的残差,反方向是找不到的。由于线性模型和非线性加性噪声模型都是后非线性模型的特例,所以这种情况下这两种模型也都是适用的,能够找出因果方向。
给出两个变量,能通过上述方法找到它们的因果方向。但更多情况下需要解决下面的问题:例如在心理学领域,通过问卷的形式收集到了一些问题的答案(xi),这些答案之间是有依赖关系的,也不会认为这些答案之间有直接的因果关系。
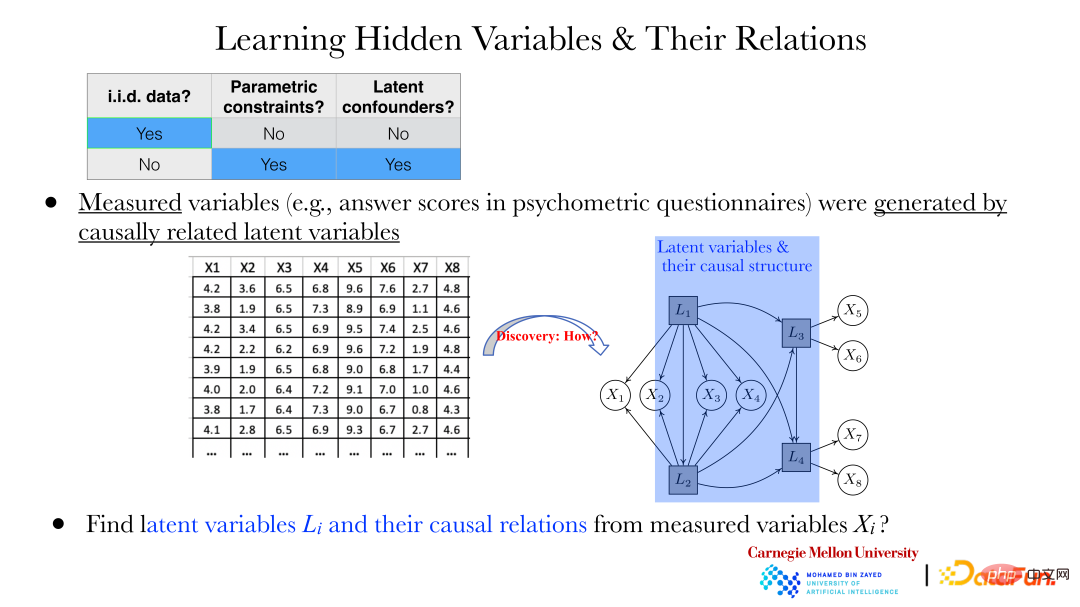
但如上图所示,这些 xi 是由背后的隐变量 Li 一起产生的。如何通过观察到的 xi 将其背后的隐变量 Li 及隐变量间关系揭示出来,就显得尤为重要。

最近这些年有一些方法能帮助我们寻找这些因变量以及它们的关系。上图则展示了泛化独立噪声(GIN,Generalized Independent Noise)方法的应用例子,该方法可以解决一系列的问题。数据内容是教师的职业倦怠情况,包含有 28 个变量。右图则展示了专家提出的可能存在的导致这些职业倦怠情况(观察到的变量)的隐变量,及隐变量间的关系。通过 GIN 方法分析观察数据得到的结果与专家给出的结果吻合。专家是通过定性的背景知识进行分析的,数据分析的定量分析方式给专家结果提供了验证和支撑。
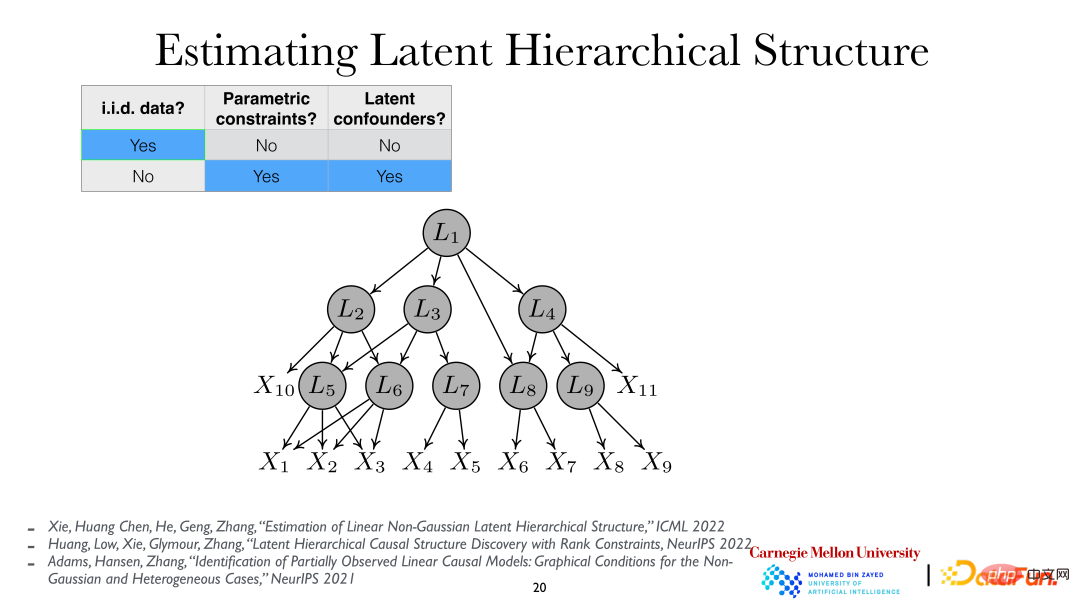
进一步深入分析,可以假设隐变量是分层的,即隐变量层级结构(Latent Hierarchical Structure)。通过分析观察变量 xi ,就能将背后的隐变量 Li 及其关系揭示出来。
三、从时间序列进行因果表征学习
了解了独立同分布情形下的因果表征方法,接下来将介绍如何在非线性条件下,独立同分布情形下,如何找到背后的隐变量及因果关系。总体来说,独立同分布情形下,需要比较强的条件(包括参数模型假设、线性模型、稀疏图等)才能找到其中的因果关系。而其他情况下可以更轻松的找到因果关系。

下面将介绍如何从时间序列中找出因果表征,即在数据不独立但是同分布的情形下,如何进行因果分析:

如果因果关系发生在观察到的时间序列上,这是经典的从时间序列数据找寻因果关系的问题,即格兰杰因果关系(Granger causality)。格兰杰因果关系与之前提到的基于条件独立的因果关系是吻合的,只是加上了时间上的限制(如果不能比因发生得早),进一步还能引进瞬时因果连接(instantaneous causal relations)。
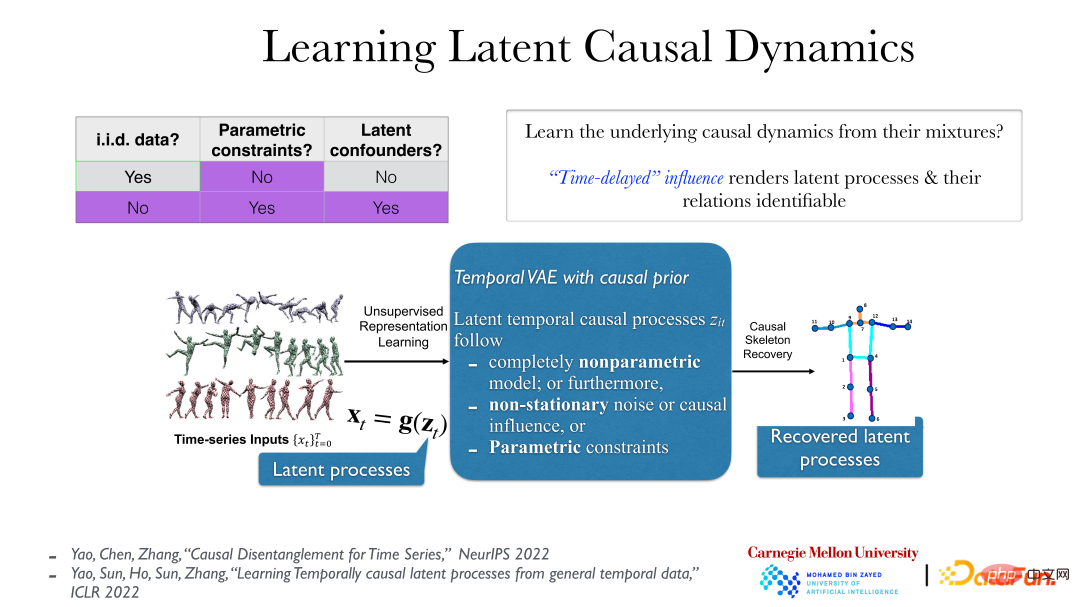
上图展示了更加具有实用性的方法。在视频数据中,数据背后真正有意义的隐藏过程(latent process),我们观察的数据,作为它们的反应(reflection),由他们的一个可逆光滑非线性函数变换产生。真正的隐因果过程一般是有时间上的因果联系的,如“推一下,然后倒下”,这个因果影响一般是有时滞(time-delayed)的。这些条件下,即使是在非常弱的假设下(即使背后的隐过程是非参数的,且 g 函数(从隐过程到观察到的时间序列)也是非参数的),也能完全将背后的隐过程全部揭示出来。
这是因为在恢复到真正的隐过程后,没有瞬时因果关系和依赖,物体(objects)之间的关系会比较清晰。但如果使用错误的分析方式去看观察数据,如直接观察视频数据的像素(pixel),会发现它们之间是存在瞬时依赖关系的。
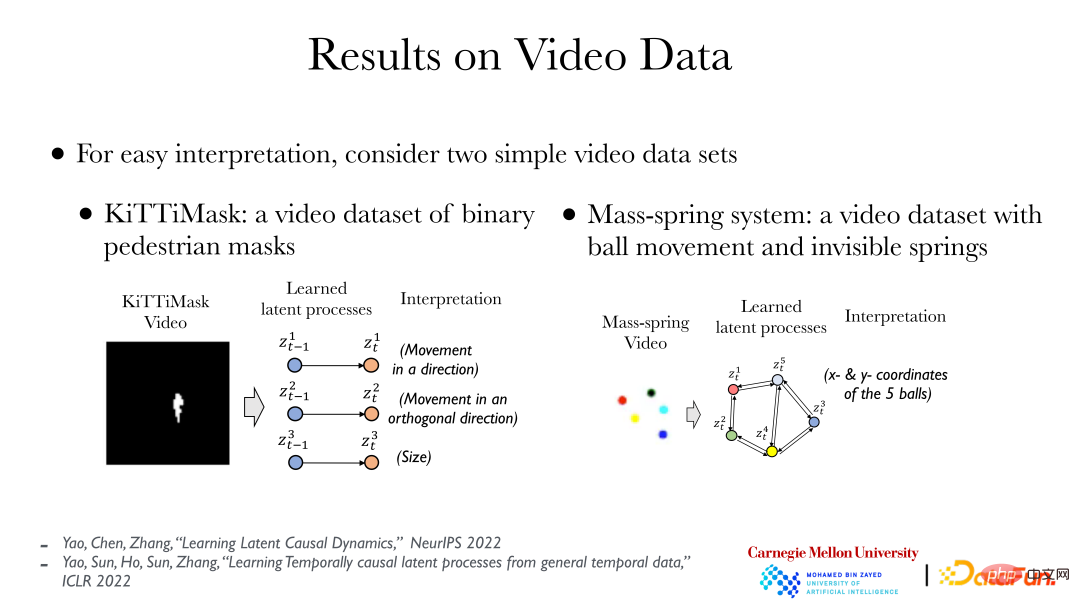
上图展示了两个简单的案例:左边展示了 KiTTiMask 视频数据,分析视频数据得到了三个隐过程:在一个方向移动;在垂直方向移动;mask 大小改变。右边展示了 5 个不同颜色的小球,某些球之间有弹簧连接(不可见),通过分析可以得到 10 个隐变量(5 个小球的 x,y 坐标),然后找到它们间的因果关系(某些小球之间有弹簧)。基于视频数据,直接只用完全非监督的方式,引入因果原则,就能找到背后对象(objects)间的关系。
四、多分布下的因果表征学习
最后介绍一下当数据分布发生变化时的因果分析:

当随时间记录变量/过程时,经常会发现数据分布会随时间变化,这是由于背后没有观察/测量到的变量的值发生了变化,由此作为反应的观察变量的数据分布就发生了变化。类似地,如果在不同条件下测量数据,会发现不同条件/地点测量到的数据的分布也可能不一样。
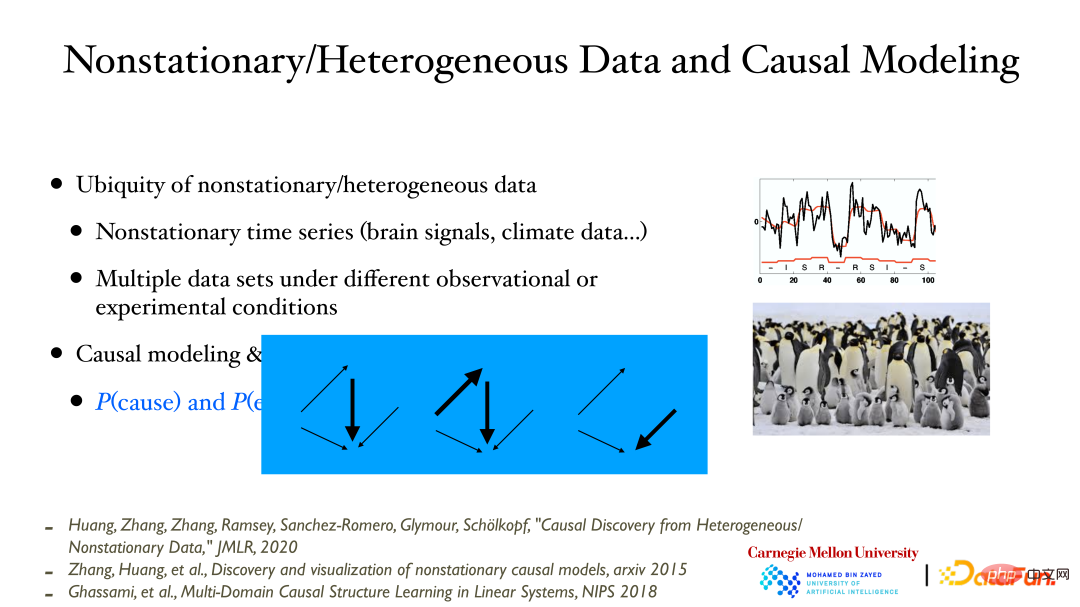
这里要强调的一点是,因果建模和数据分布发生变化是存在非常紧密联系的。当给出一个因果模型,基于模块化的性质,这些子模块可以独立发生变化,如果能从数据中观察到这个变化就能验证因果模型的正确性。这里所说的因果模型的变化是指,因果影响可以变强/变弱甚至消失。
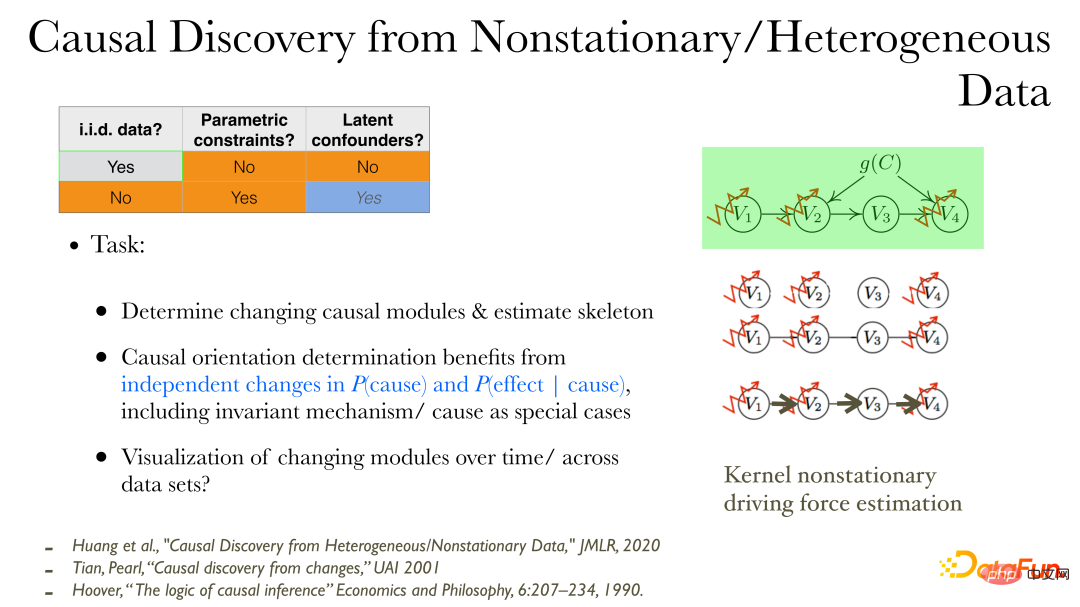
在非稳态(nonstationary)数据/异质(heterogeneous)数据中能更直接的发掘因果关系,在给出观察变量后:
① 首先可以观察发现在哪些变量的因果产生过程会发生变化;
② 把因果影响的无向边(skeleton)确定下来;
③ 找出因果方向:在数据分布发生变化时,可以使用额外的性质:因的变化与果根据因的变化间是相互独立没有联系的。因为不同模块间的变化是独立的;
④ 使用低维可视化方法描述因果变化的过程。
下图展示了对纽约证券交易所中股票 daily return 数据(瞬时数据,没有时滞性)进行分析的部分结果:
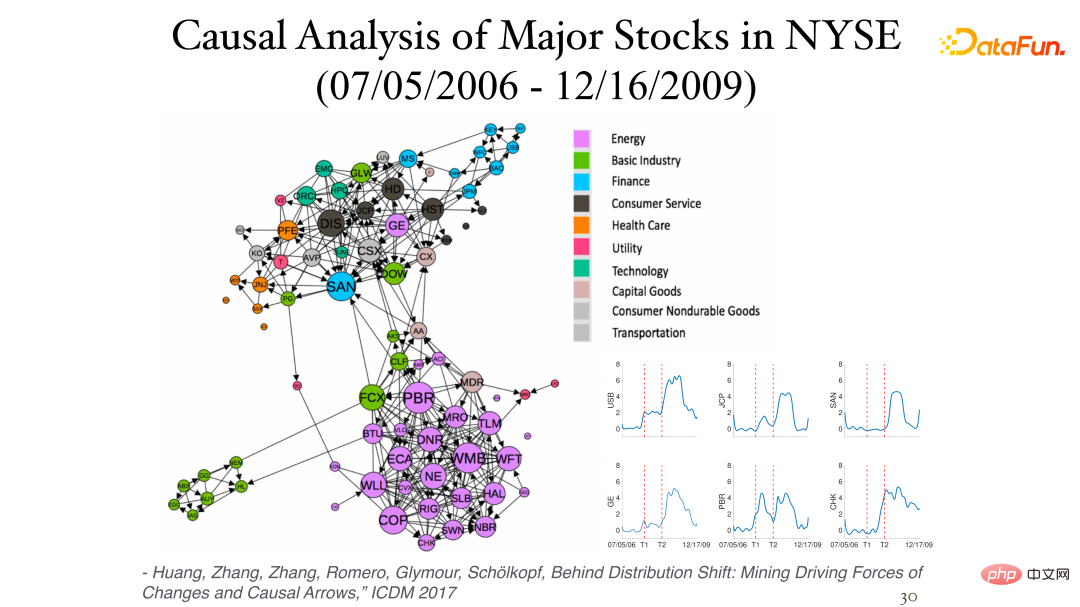
通过非稳态性可以找出它们之间不对称性的影响。不同的 sector 往往是一类(cluster),且紧密的联系在一起。右下角图片展示了股票随时间变化的因果过程,其中两条纵轴分别表示了 2007 年和 2008 年经融危机。
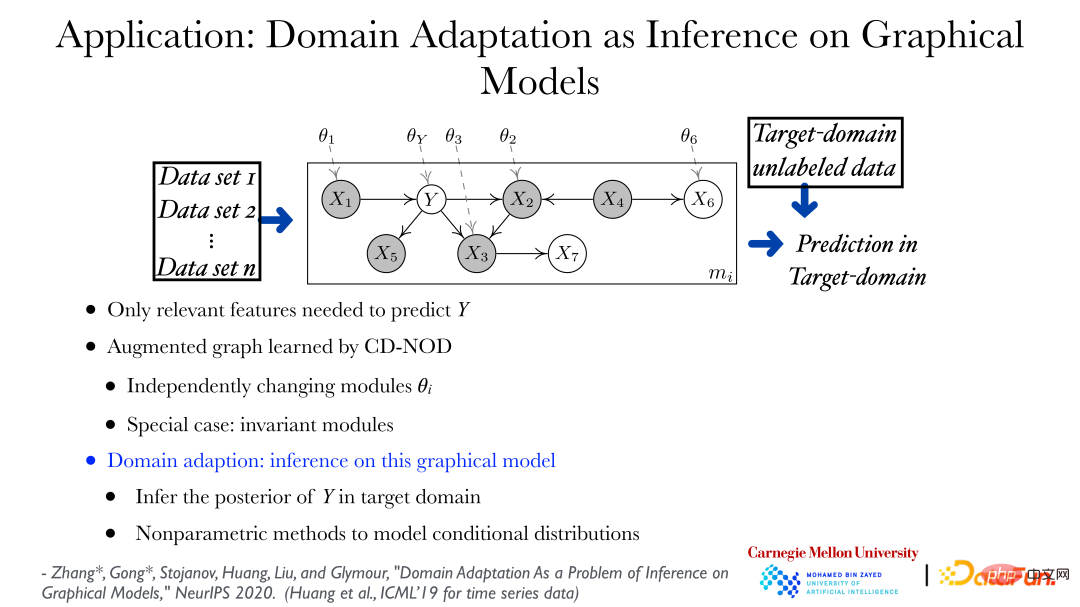
通过多分布条件下的因果分析方法可以从不同的数据集中找到数据的变化规律,直接应用就可以进行迁移学习,进行领域适用(domain adaptation)。如上图所示,可以从不同的数据集中找出数据的变化规律,并通过增广图(augmented graph)来表示数据的分布可以发生怎样的变化,如图中 theta_Y 是表示,Y 在给出它的父亲节点下的分布可以根据其领域(domain)不同而发生变化。基于描述数据分布发生变化的图,在一个新的领域或者目标领域预测 Y 就是一个非常标准的问题,即给出特征(feature)值如何找出Y的后验概率,是一个推理(inference)问题。
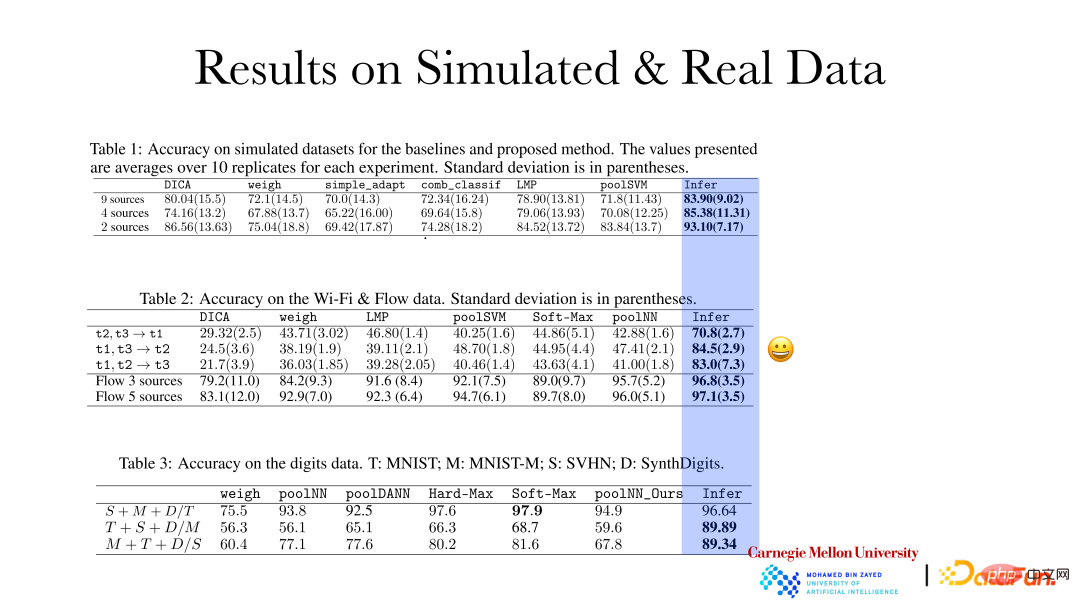
上图展示了因果表征方法在模拟(simulated)数据和真实(real)数据上的推理效果准确率是有明显提升的。基于定性的变化规律和不同领域的变化性的大小,在新领域出现时再进行适应性调整,这样的预测效果会比较好。

上图展示了最近的部分解纠缠的领域适应(Partial Disentanglement for Domain Adaption)相关工作。已知特征(feature)和目标(target),假设一切都是非参数的,且有一些因子(factor)随领域(domain)是不发生变化的即分布是稳定的,但有个别因子可能发生变化,希望找到这些极少数的分布发生变化的因子。基于找到的因子,就可以将不同领域对齐(align)到一起,然后找到不同领域的对应关系,这样在进行领域适应/迁移学习时就会水到渠成。可以证明导致分布发生变化的背后独立的因子,是可以直接从观察数据中恢复出来的,不变化的这部分因子可以恢复其 subspace。如表格所示,通过以上方法在领域适应中能取得很好的效果。同时,这个方法也符合最小变化(minimal change)的原则,即希望用最少变化的因子来解释不同领域数据的因子到底发生了怎样的变化,从而将它们对应起来。

总结一下,本次分享主要包含了以下内容:
① 一系列的机器学习问题需要一个合适的关于数据的背后表征。如决策时希望知道决策的影响,基于此才能做出最优的决策;在领域适应/泛化中希望知道数据的分布发生了怎样的变化,从而做出最优预测;在强化学习中,agent 与环境的交互以及交互带来的 reward 本身就是一个因果问题;推荐系统也是一个因果问题,因为 user 是被改变的;可信赖 AI、可解释 AI 以及公平性都和因果表征有关。
② 因果性,包括隐变量,在一定条件下是可以从数据中完全恢复出来的。可以真正通过数据理解背后过程的性质,然后加以使用。
③ 因果关系不是神秘的。只要有数据,只要假设是合适的,就能找出背后的因果性。这里所做出的假设最好是可以验证的。
总体来说,因果表征学习有非常大的应用前景,同时有很多方法也亟待开发,需要大家共同努力。
以上是CMU张坤:因果表征技术最新进展的详细内容。更多信息请关注PHP中文网其他相关文章!
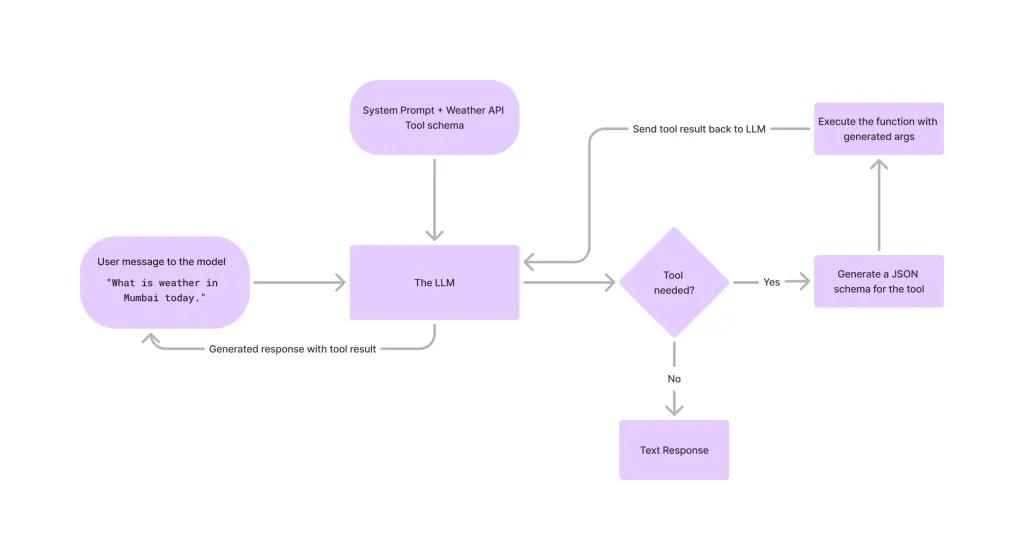 在LLMS中调用工具Apr 14, 2025 am 11:28 AM
在LLMS中调用工具Apr 14, 2025 am 11:28 AM大型语言模型(LLMS)的流行激增,工具称呼功能极大地扩展了其功能,而不是简单的文本生成。 现在,LLM可以处理复杂的自动化任务,例如Dynamic UI创建和自主a
 多动症游戏,健康工具和AI聊天机器人如何改变全球健康Apr 14, 2025 am 11:27 AM
多动症游戏,健康工具和AI聊天机器人如何改变全球健康Apr 14, 2025 am 11:27 AM视频游戏可以缓解焦虑,建立焦点或支持多动症的孩子吗? 随着医疗保健在全球范围内挑战,尤其是在青年中的挑战,创新者正在转向一种不太可能的工具:视频游戏。现在是世界上最大的娱乐印度河之一
 没有关于AI的投入:获胜者,失败者和机遇Apr 14, 2025 am 11:25 AM
没有关于AI的投入:获胜者,失败者和机遇Apr 14, 2025 am 11:25 AM“历史表明,尽管技术进步推动了经济增长,但它并不能自行确保公平的收入分配或促进包容性人类发展,”乌托德秘书长Rebeca Grynspan在序言中写道。
 通过生成AI学习谈判技巧Apr 14, 2025 am 11:23 AM
通过生成AI学习谈判技巧Apr 14, 2025 am 11:23 AM易于使用,使用生成的AI作为您的谈判导师和陪练伙伴。 让我们来谈谈。 对创新AI突破的这种分析是我正在进行的《福布斯》列的最新覆盖范围的一部分,包括识别和解释
 泰德(Ted)从Openai,Google,Meta透露出庭,与我自己自拍Apr 14, 2025 am 11:22 AM
泰德(Ted)从Openai,Google,Meta透露出庭,与我自己自拍Apr 14, 2025 am 11:22 AM在温哥华举行的TED2025会议昨天在4月11日举行了第36版。它有来自60多个国家 /地区的80个发言人,包括Sam Altman,Eric Schmidt和Palmer Luckey。泰德(Ted)的主题“人类重新构想”是量身定制的
 约瑟夫·斯蒂格利兹(Joseph StiglitzApr 14, 2025 am 11:21 AM
约瑟夫·斯蒂格利兹(Joseph StiglitzApr 14, 2025 am 11:21 AM约瑟夫·斯蒂格利茨(Joseph Stiglitz)是2001年著名的经济学家,是诺贝尔经济奖的获得者。斯蒂格利茨认为,AI可能会使现有的不平等和合并权力恶化,并在几个主导公司的手中加剧,最终破坏了经济的经济。
 什么是图形数据库?Apr 14, 2025 am 11:19 AM
什么是图形数据库?Apr 14, 2025 am 11:19 AM图数据库:通过关系彻底改变数据管理 随着数据的扩展及其特征在各个字段中的发展,图形数据库正在作为管理互连数据的变革解决方案的出现。与传统不同
 LLM路由:策略,技术和Python实施Apr 14, 2025 am 11:14 AM
LLM路由:策略,技术和Python实施Apr 14, 2025 am 11:14 AM大型语言模型(LLM)路由:通过智能任务分配优化性能 LLM的快速发展的景观呈现出各种各样的模型,每个模型都具有独特的优势和劣势。 有些在创意内容gen上表现出色


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

SublimeText3汉化版
中文版,非常好用

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。

EditPlus 中文破解版
体积小,语法高亮,不支持代码提示功能

DVWA
Damn Vulnerable Web App (DVWA) 是一个PHP/MySQL的Web应用程序,非常容易受到攻击。它的主要目标是成为安全专业人员在合法环境中测试自己的技能和工具的辅助工具,帮助Web开发人员更好地理解保护Web应用程序的过程,并帮助教师/学生在课堂环境中教授/学习Web应用程序安全。DVWA的目标是通过简单直接的界面练习一些最常见的Web漏洞,难度各不相同。请注意,该软件中






