Python实现LR经典算法

零到壹度原创: 2018-04-19 16:55:445668浏览

本文实例讲述了Python实现LR经典算法。分享给大家供大家参考，具体如下：

（一）认识Logistic回归（LR）分类器

首先，Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题，利用Logistic函数（或称为Sigmoid函数），自变量取值范围为(-INF, INF)，自变量的取值范围为(0,1)，函数形式为：

由于sigmoid函数的定义域是(-INF, +INF),而值域为(0, 1)。因此最基本的LR分类器适合于对两分类（类0，类1）目标进行分类。Sigmoid 函数是个很漂亮的“S”形，如下图所示：

LR分类器(Logistic Regression Classifier)目的就是从训练数据特征学习出一个0/1分类模型--这个模型以样本特征的线性组合作为自变量，使用logistic函数将自变量映射到(0,1)上。因此LR分类器的求解就是求解一组权值（是是名义变量--dummy，为常数，实际工程中常另x0=1.0。不管常数项有没有意义，最好保留），并代入Logistic函数构造出一个预测函数：

函数的值表示结果为1的概率，就是特征属于y=1的概率。因此对于输入x分类结果为类别1和类别0的概率分别为：

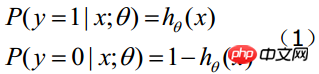
当我们要判别一个新来的特征属于哪个类时，按照下式求出一个z值：

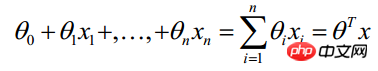（x1,x2,...,xn是某样本数据的各个特征，维度为n）

进而求出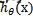---若大于0.5就是y=1的类，反之属于y=0类。（注意：这里依然假设统计样本是均匀分布的，所以设阈值为0.5）。LR分类器的这一组权值如何求得的呢？这就需要涉及到极大似然估计MLE和优化算法的概念了，数学中最优化算法常用的就是梯度上升（下降）算法。

Logistic回归可以也可以用于多分类的，但是二分类的更为常用也更容易解释。所以实际中最常用的就是二分类的Logistic回归。LR分类器适用数据类型：数值型和标称型数据。其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。

（二）Logistic回归数学推导

1，梯度下降法求解Logistic回归

首先，理解下述数学推导过程需要较多的导数求解公式，可以参考“常用基本初等函数求导公式积分公式”。

假设有n个观测样本，观测值分别为设为给定条件下得到yi=1的概率。在同样条件下得到yi=0的条件概率为。于是，得到一个观测值的概率为

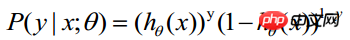-----此公式实际上是综合公式（1）得出

因为各项观测独立，所以它们的联合分布可以表示为各边际分布的乘积：

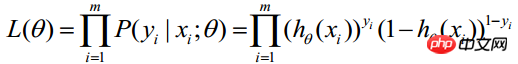（m表统计样本数目）

上式称为n个观测的似然函数。我们的目标是能够求出使这一似然函数的值最大的参数估计。于是，最大似然估计的关键就是求出参数，使上式取得最大值。

对上述函数求对数：

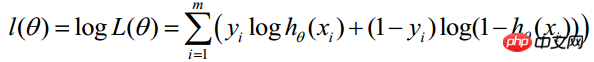
最大似然估计就是求使上式取最大值时的θ，这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。在Andrew Ng的课程中将J(θ)取为下式，即：J(θ)=-(1/m)l(θ)，J(θ)最小值时的θ则为要求的最佳参数。通过梯度下降法求最小值。θ的初始值可以全部为1.0，更新过程为：

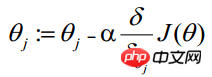（j表样本第j个属性，共n个；a表示步长--每次移动量大小，可自由指定）

因此，θ（可以设初始值全部为1.0）的更新过程可以写成：

（i表示第i个统计样本，j表样本第j个属性；a表示步长）

该公式将一直被迭代执行，直至达到收敛（在每一步迭代中都减小，如果某一步减少的值少于某个很小的值（小于0.001）, 则其判定收敛）或某个停止条件为止（比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围）。

2，向量化Vectorization求解

Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。如上式，Σ(...)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。下面介绍向量化的过程：

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知hθ(x)-y可由g(A)-y一次计算求得。

θ更新过程可以改为：

综上所述，Vectorization后θ更新的步骤如下：

（1）求A=X*θ(此处为矩阵乘法，X是（m,n+1）维向量，θ是（n+1，1）维列向量，A就是（m,1）维向量)

（2）求E=g(A)-y（E、y是（m,1）维列向量）

（3）求（a表示步长）

3，步长a的选择

a的取值也是确保梯度下降收敛的关键点。值太小则收敛慢，值太大则不能保证迭代过程收敛（迈过了极小值）。要确保梯度下降算法正确运行，需要保证 J(θ)在每一步迭代中都减小。如果步长a取值正确，那么J(θ)应越来越小。所以a的取值判断准则是：如果J(θ)变小了表明取值正确，否则减小a的值。

选择步长a的经验为：选取一个a值，每次约3倍于前一个数，如果迭代不能正常进行（J增大了，步长太大，迈过了碗底）则考虑使用更小的步长，如果收敛较慢则考虑增大步长，a取值示例如：

…, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1…。

4，特征值归一化

Logistic 回归也是一种回归算法，多维特征的训练数据进行回归采取梯度法求解时其特征值必须做scale，确保特征的取值范围在相同的尺度内计算过程才会收敛（因为特征值得取值范围可能相差甚大，如特征1取值为（1000-2000），特征2取值为（0.1-0.2））。feature scaling的方法可自定义，常用的有：

1) mean normalization (or standardization)

(X - mean(X))/std(X)，std(X)表示样本的标准差

2) rescaling

(X - min) / (max - min)

5，算法优化--随机梯度法

梯度上升（下降）算法在每次更新回归系数时都需要遍历整个数据集, 该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度算法。由于可以在新样本到来时对分类器进行增量式更新，它可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批处理运算，因而随机梯度算法是一个在线学习算法。（与“在线学习”相对应，一次处理所有数据被称作是“批处理”）。随机梯度算法与梯度算法的效果相当，但具有更高的计算效率。

（三）Python实现Logistic回归算法

上节通过Andrew Ng的课程对J(θ)=-(1/m)l(θ)采取梯度下降法求解说明了Logistic回归的求解过程，本节Python实现算法的过程依然直接对J(θ)采取梯度上升法或者随机梯度上升法求解，LRTrain对象同时实现了采取梯度上升法或者随机梯度上升法求解过程。

LR分类器学习包中包含lr.py/object_json.py/test.py三个模块。lr模块通过对象logisticRegres实现了LR分类器，支持gradAscent('Grad') and randomGradAscent('randomGrad')两种求解方法（二选一，classifierArray只存储一种分类求解结果，当然你也可以定义两个classifierArray同时支持两种求解方法）。

test模块中是利用LR分类器根据疝气病症预测病马死亡率的应用。该数据存在一个问题--数据由30%的丢失率，这里采用特殊值0替代，因为0不会影响LR分类器的权值更新。

训练数据中样本特征值的部分缺失是很棘手的问题，很多文献致力于解决该问题，因为数据直接丢掉太可惜，重新获取代价也昂贵。一些可选的数据丢失处理方法包括：

□使用可用特征的均值来填补缺失值；

□使用特殊值来±真补缺失值，如-1;

□忽略有缺失值的样本；

□使用相似样本的均值添补缺失值；

□使用另外的机器学习算法预测缺失值。

LR分类器算法学习包下载地址是：

machine learning Logistic regression

（四）Logistic回归应用

Logistic回归的主要用途：

寻找危险因素：寻找某一疾病的危险因素等；

预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；

判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。