用於時間序列機率預測的分位數迴歸

不要改變原內容的意思，微調內容，重寫內容，不要續寫。 「分位數迴歸滿足此需求，提供具有量化機會的預測區間。它是一種統計技術，用於模擬預測變數與反應變數之間的關係，特別是當反應變數的條件分佈命令人感興趣時。迴歸

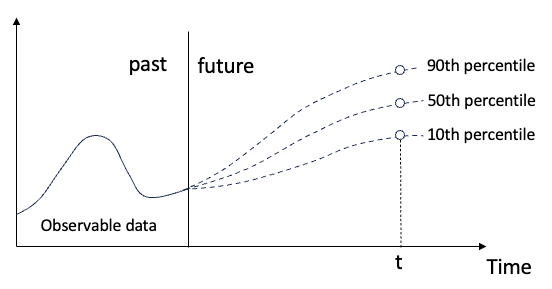分位數迴歸概念 分位數迴歸是估計⼀組迴歸變數X與被解釋變數Y的分位數之間線性關係的建模⽅法。

現有的迴歸模型其實是研究被解釋變數與解釋變數之間關係的一種方法。他們關註解釋變數與被解釋變數之間的關係及其誤差分佈的情況，其中位數迴歸和分位數迴歸是兩種常見的迴歸模型。它們是根據Koenker和Bassett (1978) 首次提出的。

普通最小平方法迴歸估計量的計算是基於最小化殘差平方和。分位數迴歸估計量的計算也是基於種對稱形式的絕對值殘差最小化。其中，中位數迴歸運算的是最絕對值差估計（LAD，least absolute deviations estimator）。

分位數迴歸的優點 

解釋被解釋變數條件分佈的全貌，不只是分析解釋變數的條件期望值（平均數），也可分析解釋變數如何影響被解釋變數的中位數、分位數等。不同分位數下的迴歸係數估計值常常不同，即解釋變數對不同分位數的影響效果不同，因此解釋變數不同分位數的影響不同會對被解釋變數的影響產生不同。

進行中位數迴歸的估計法與最小乘法相比，估計結果對離群值則表現的更加穩健，且分位數迴歸對誤差項並不要求很強的假設條件，因此對於非常態狀態下的分佈，中位數迴歸系數量則較為健康。同時，分位數迴歸系統量估計則加穩健。

分位數迴歸相對於蒙特卡羅模擬有哪些優勢呢？首先，分位數迴歸直接估計給定預測因子的反應變數的條件量值。這意味著，它不像蒙特卡羅模擬那樣產生大量可能的結果，而是提供了反應變數分佈的特定量級的估計值。這對於了解不同層次的預測不確定性特別有用，例如二分位數、四分位數或極端量值。其次，分位數迴歸提供了一種基於模型的預測不確定性估算方法，利用觀測資料來估計變數之間的關係，並根據此關係進行預測。相較之下，蒙特卡羅模擬依賴為輸入變數指定機率分佈，並根據隨機抽樣產生結果。

NeuralProphet提供兩種統計技術：（1）分位數迴歸和（2）保形分位數迴歸。共形分位數預測技術增加了一個校準過程來做分位數迴歸。在本文中，我們將使用Neural Prophet的分位數迴歸模組來做分位數迴歸預測。這個模組增加了一個校準過程，來確保預測結果與觀測資料的分佈一致。我們將在本章中使用Neural Prophet的分位數回歸模組。

環境需求

安裝 NeuralProphet。

!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

導入需要的函式庫。

%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")

資料集

共享單車資料。該資料集是一個多變量資料集，包含每日租賃需求以及溫度或風速等其他天氣領域。

data = pd.read_csv('/bike_sharing_daily.csv')data.tail()

圖(B): 共享單車

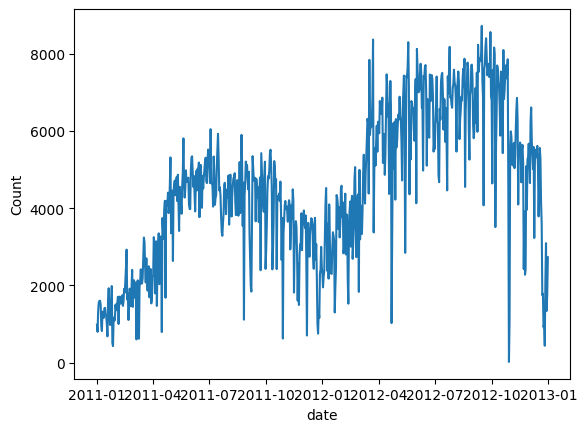
繪製共享單車的數量圖。我們觀察到，需求量在第二年增加，而且有季節性規律。

# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()

圖 (C)：自行車租賃日需求量

為建模做最基本的資料準備。 NeuralProphet 要求列名為 ds 和 y，這與 Prophet 的要求相同。

df = data[['ds','cnt']]df.columns = ['ds','y']

构建分位数回归模型

直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打开参数 quantiles = quantile_list。

from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()

分位数回归预测

我们将使用 .make_future_dataframe()为预测创建新数据帧，NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100，只包含过去的 100 个数据点。如果设置为 True，则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。

future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)

预测结果存储在数据框架 predict 中。

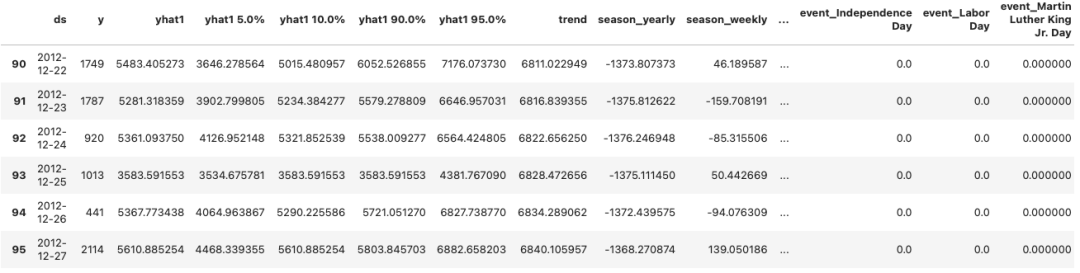图 (D)：预测

上述数据框架包含了绘制地图所需的所有数据元素。

m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")

预测区间是由分位数值提供的！

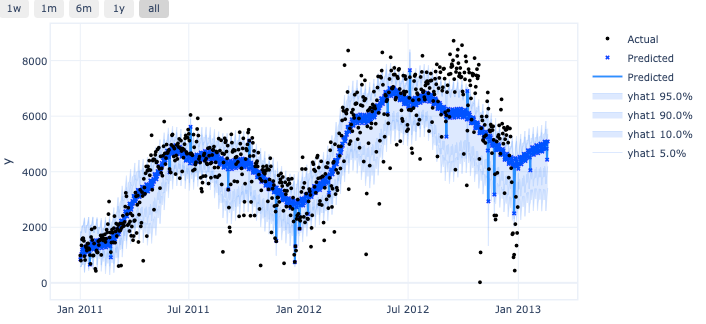图 (E)：分位数预测

预测区间和置信区间的区别

预测区间和置信区间在流行趋势中很有帮助，因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中，我在左边画出了线性回归，在右边画出了分位数回归。

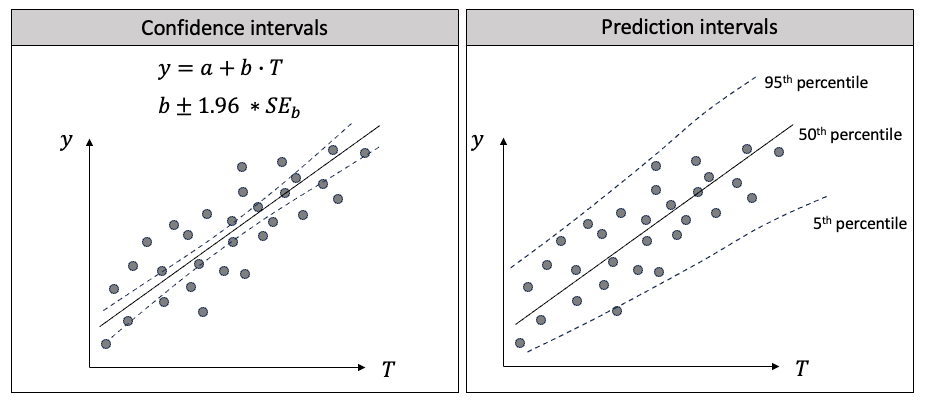图(F)：置信区间与预测区间的区别

首先，它们的目标不同：

• 线性回归的主要目标是找到一条线，使预测值尽可能接近给定自变量值时因变量的条件均值。
• 分位数回归旨在提供未来观测值的范围，在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。

其次，它们的计算方法不同：

• 在线性回归中，置信区间是对自变量系数的区间估计，通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
• 在分位数回归中，你可以选择依赖变量的不同量级来估计回归系数，通常是最小化绝对偏差的加权和，而不是使用OLS方法。

第三，它们的应用不同：

• 在线性回归中，预测的条件均值有 95% 的置信区间。置信区间较窄，因为它是条件平均值，而不是整个范围。
• 在分位数回归中，预测值有 95% 的概率落在预测区间的范围内。

写在最后

本文介绍了分位数回归预测区间的概念，以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异，这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术，即复合分位数回归（CQR），用于预测不确定性。

以上是用於時間序列機率預測的分位數迴歸的詳細內容。更多資訊請關注PHP中文網其他相關文章！