Makridakis M-Competitions系列(分別稱為M4和M5)分別在2018年和2020年舉辦(M6也在今年舉辦了)。對於那些不了解的人來說,m系列得比賽可以被認為是時間序列生態系統的一種現有狀態的總結,為當前得預測的理論和實踐提供了經驗和客觀的證據。
2018年M4的結果表明,純粹的「 ML」方法在很大程度上勝過傳統的統計方法,這在當時是出乎意料的。在兩年後的M5[1]中,最的高分是僅有「 ML」方法。而所有前50名基本上都是基於ML的(大部分是樹型模型)。這場比賽看到了LightGBM(用於時間序列預測)以及Amazon's Deepar [2]和N-Beats [3]的首次亮相。 N-Beats模型於2020年發布,並且優於M4比賽的獲勝者3%!
最近的 Ventilator Pressure Prediction比賽展示了使用深度學習方法來應對即時時間序列挑戰的重要性。比賽的目的是預測機械肺內壓力的時間順序。每個訓練實例都是自己的時間序列,因此任務是一個多個時間序列的問題。獲勝團隊提交了多層深度架構,其中包括LSTM網路和Transformer 區塊。
在過去的幾年中,許多著名的架構已經發布,如MQRNN和DSSM。所有這些模型都利用深度學習為時間序列預測領域貢獻了許多新東西。除了贏得Kaggle比賽,也為我們帶來了更多的進步例如:
- 多功能性:將模型用於不同任務的能力。
- MLOP:在生產中使用模型的能力。
- 解釋性與解釋性:黑盒子模型並不那麼受歡迎。
本文討論了5種專門研究時間序列預測的深度學習體系結構,論文是:
- N-BEATS(ElementAI)
- DeepAR (Amazon)
- Spacetimeformer[4]
- Temporal Fusion Transformer or TFT(Google) [5]
- TSFormer(時間序列中的MAE)[7]
N-BEATS
這種模式直接來自於(不幸的)短暫的ElementAI公司,該公司是由Yoshua Bengio共同創立的。頂層架構及其主要元件如圖1所示:

N-BEATS是一個純粹的深度學習架構,它基於整合前饋網路的深度堆疊,這些網絡也透過正向和反向的相互連接進行堆疊。
每一個區塊只對前一個的backcast所產生的殘差進行建模,然後基於該誤差更新預測。該過程模擬了擬合ARIMA模型時的Box-Jenkins方法。
以下是該模型的主要優勢:
表達性強且易於使用:該模型易於理解,具有模組化結構,它被設計為需要最小的時間序列特徵工程並且不需要對輸入進行縮放。
此模型具有對多個時間序列進行概括的能力。換句話說,分佈略有不同的不同時間序列可以用作輸入。在N-BEATS中是透過元學習實現的。元學習過程包括兩個過程:內部學習過程和外部學習過程。內部學習過程發生在區塊內部,並幫助模型捕捉局部時間特徵。外部學習過程發生在堆疊層,幫助模型學習所有時間序列的全局特徵。
雙重殘差疊加:殘差連接和疊加的想法是非常巧妙的,它幾乎被用於每種類型的深度神經網路。在N-BEATS的實作中應用了相同的原理,但有一些額外的修改:每個區塊有兩個殘差分支,一個運行在回看視窗(稱為backcast),另一個運行在預測視窗(稱為forecast)。
每一個連續的區塊只對前一個區塊重建的backcast所產生的殘差進行建模,然後基於該誤差更新預測。這有助於模型更好地逼近有用的後推訊號,同時最終的堆疊預測預測被建模為所有部分預測的分層和。就是這個過程模擬了ARIMA模型的Box-Jenkins方法。
可解釋性:模型有兩種變體,通用的和可解釋性的。在通用變體中,網路任意學習每個區塊的全連接層的最終權值。在可解釋的變體中,每個區塊的最後一層被刪除。然後將後推backcast和預測forecast分支乘以模擬趨勢(單調函數)和季節性(週期性循環函數)的特定矩陣。
注意:原始的N-BEATS實作只適用於單變數時間序列。
DeepAR
結合深度學習和自回歸特性的新穎時間序列模型。圖2顯示了DeepAR的頂層架構:

以下是該模型的主要優勢:
DeepAR在多個時間序列上工作得非常好:透過使用多個分佈略有不同的時間序列來建構全域模型。也適用於許多現實場景。例如電力公司可能希望為每個客戶推出電力預測服務,每個客戶都有不同的消費模式(這意味著不同的分佈)。
除了歷史數據,DeepAR還允許使用已知的未來時間序列(自回歸模型的一個特點)和額外的靜態屬性。在前面提到的電力需求預測場景中,一個額外的時間變數可以是月份(作為一個整數,值在1-12之間)。假設每個客戶都與一個測量功耗的感測器相關聯,那麼額外的靜態變數將是sensor_id或customer_id之類的東西。
如果莫熟悉使用MLPs和rnn等神經網路架構進行時間序列預測,那麼一個關鍵的預處理步驟是使用標準化或標準化技術對時間序列進行縮放。這在DeepAR中是不需要手動操作的,因為底層的模型對每個時間序列i的自回歸輸入z進行縮放,縮放因子為v_i,即該時間序列的平均值。具體而言,論文基準中使用的比例因子方程式如下:

但是在實務中,如果目標時間序列的大小差異很大,那麼在預處理過程中應用自己的縮放還是有必要的。例如,在能源需求預測情境中,資料集可以包含中壓電力客戶(例如小型工廠,按兆瓦單位消耗電力)和低壓客戶(例如家庭,按千瓦單位消耗電力)。
DeepAR進行機率預測,而不是直接輸出未來值。這是以蒙特卡洛樣本的形式完成的。這些預測被用來計算分位數預測,透過使用分位數損失函數。對於不熟悉這種損失類型的人,分位數損失不僅用來計算一個估計,而且用來計算圍繞該值的預測區間。
Spacetimeformer
在單變數時間序列中時間依賴性是最重要的。但在多個時間序列場景中,事情就沒那麼簡單了。例如假設我們有一個天氣預報任務,想要預測五個城市的溫度。讓我們假設這些城市屬於一個國家。鑑於目前所看到的,我們可以使用DeepAR並將每個城市作為外部靜態協變量進行建模。
換句話說,該模型將同時考慮時間和空間關係。這就是Spacetimeformer的核心理念:使用一個模型來利用這些城市/地點之間的空間關係,從而學習額外的有用依賴,因為模型將同時考慮時間和空間關係。
深入研究時空序列
顧名思義,這種模型在內部使用了基於transformers的結構。在使用基於transformers的模型進行時間序列預測時,一種流行的產生時間感知嵌入的技術是透過Time2Vec[6]嵌入層傳遞輸入(對於NLP任務是使用位置編碼向量來取代Time2Vec)。雖然這種技術對於單變量時間序列非常有效,但對於多變量時間輸入卻沒有任何意義。可能是在語言建模中,句子中的每個單字都用嵌入來表示,單字本質上是一個是詞彙表的一部分,而時間序列則沒那麼簡單。
在多元時間序列中,在給定的時間步長t,輸入的形式為x_1,t, x2,t, x_m,t其中x_i,t是特徵i的數值,m是特徵/序列的總數。如果我們將輸入通過一個Time2Vec層,將產生時間嵌入向量。這種嵌入真正代表什麼?答案是它將把整個輸入集合表示為單一實體(令牌)。因此模型將只學習時間步之間的時間動態,但將錯過特徵/變數之間的空間關係。
Spacetimeformer解決了這個問題,它將輸入扁平化為一個大向量,稱為時空序列。如果輸入包含N個變量,組織成T個時間步,則產生的時空序列將具有(NxT)標記。下圖3更好地顯示了這一點:

論文指出:「(1)包含時間資訊的多元輸入格式。解碼器輸入缺少(“?”)值,在進行預測時設為零。(2)時間序列透過一個Time2Vec層,產生一個代表週期性輸入模式的頻率嵌入。(3)二進位嵌入表示該值是作為上下文給出的還是需要預測的。(4)將每個時間序列的整數索引映射到一個具有查找表嵌入的「空間」表示。(5)利用前饋層投影每個時間序列的Time2Vec嵌入和變數值。(6)將值和時間,變數和給定的嵌入求和會導致使MSA在時間和可變空間之間以更長的序列作為輸入。
換句話說,最後的序列編碼了一個包含了時間、空間和上下文訊息統一的嵌入。但是這種方法的一個缺點是,序列可能會變得很長導致資源的二次成長。這是因為根據注意機制,每個令牌都要對另一個進行檢查。作者使用了一種更有效的體系結構,稱為Performer注意機制,適用於更大的序列。
Temporal Fusion Transformer
Temporal Fusion Transformer(TFT)是由Google發布的基於Transformer的時間序列預測模型。TFT比以前的模型更加通用。

TFT的頂層架構如圖4所示。以下是該模型的主要優勢:
與前面提到的模型一樣,TFT支援在多個異質時間序列上建構模型。
TFT支援三種類型的特徵:i)具有已知的未來輸入的時變資料ii)僅到目前為止已知的時變資料iii)分類/靜態變量,也被稱為時不變特徵。因此TFT比以前的型號更通用。在前面提到的電力需求預測場景中,我們希望使用濕度水平作為時變特徵,這是到目前為止才知道的。這在TFT中是可行的,但在DeepAR中不行。
圖5顯示如何使用所有這些特性的範例:

- 時間序列資料的密度比自然語言資料低得多
- 我們需要比NLP資料更長的時間序列資料

我們將他總結為以下4點:
1、掩蔽
作為資料進入編碼器的前一步。輸入序列(Sᶦ)已分佈到P片中,其長度為L。因此,用於預測下一個時間步長的滑動視窗的langth是P XL。

遮蔽比率為75%(看著很高,估計是用了MAE一樣的參數); 我們要完成的是一項自監督任務,所以數據越少編碼器的計算速度就越快。
這樣做(掩蔽輸入序列段)的主要原因是:
- 段(patch)比單點好。
- 它使使用下游模型變得簡單(STGNN將單元段作為輸入)
- 可以分解編碼器的輸入大小。
class Patch(nn.Module):<br>def __init__(self, patch_size, input_channel, output_channel, spectral=True):<br>super().__init__()<br>self.output_channel = output_channel<br>self.P = patch_size<br>self.input_channel = input_channel<br>self.output_channel = output_channel<br>self.spectral = spectral<br>if spectral:<br>self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)<br>else:<br>self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))<br>def forward(self, input):<br>B, N, C, L = input.shape<br>if self.spectral:<br>spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)<br>real = spec_feat_.real<br>imag = spec_feat_.imag<br>spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)<br>output = self.emb_layer(spec_feat).transpose(-1, -2)<br>else:<br>input = input.unsqueeze(-1) # B, N, C, L, 1<br>input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1<br>output = self.input_embedding(input) # B*N, d, L/P, 1<br>output = output.squeeze(-1).view(B, N, self.output_channel, -1)<br>assert output.shape[-1] == L / self.P<br>return output
以下是產生遮蔽的函數:
class MaskGenerator(nn.Module):<br>def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):<br>super().__init__()<br>self.mask_size = mask_size<br>self.mask_ratio = mask_ratio<br>self.sort = True<br>self.average_patch = lm<br>self.distribution = distribution<br>if self.distribution == "geom":<br>assert lm != -1<br>assert distribution in ['geom', 'uniform']<br>def uniform_rand(self):<br>mask = list(range(int(self.mask_size)))<br>random.shuffle(mask)<br>mask_len = int(self.mask_size * self.mask_ratio)<br>self.masked_tokens = mask[:mask_len]<br>self.unmasked_tokens = mask[mask_len:]<br>if self.sort:<br>self.masked_tokens = sorted(self.masked_tokens)<br>self.unmasked_tokens = sorted(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def geometric_rand(self):<br>mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked<br>self.masked_tokens = np.where(mask)[0].tolist()<br>self.unmasked_tokens = np.where(~mask)[0].tolist()<br># assert len(self.masked_tokens) > len(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def forward(self):<br>if self.distribution == 'geom':<br>self.unmasked_tokens, self.masked_tokens = self.geometric_rand()<br>elif self.distribution == 'uniform':<br>self.unmasked_tokens, self.masked_tokens = self.uniform_rand()<br>else:<br>raise Exception("ERROR")<br>return self.unmasked_tokens, self.masked_tokens
2、編碼
包括了輸入嵌入,位置編碼和Transformer 區塊的。編碼器只能在未遮蔽的patchs上執行(這個也是MAE的方法)。

輸入嵌入
使用線性的投影來獲得輸入的嵌入,可將未遮蔽的空間轉換為潛在空間。它的公式可以在下面看到:

W和B是可學習的參數,U是維度中的模型輸入向量。
位置編碼
簡單的位置編碼層用於附加新的順序資訊。添加了“可學習”一詞,這有助於表現出比正弦更好的性能。因此可學習的位置嵌入顯示了時間序列的良好結果。
class LearnableTemporalPositionalEncoding(nn.Module):<br>def __init__(self, d_model, dropout=0.1, max_len: int = 1000):<br>super().__init__()<br>self.dropout = nn.Dropout(p=dropout)<br>self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)<br>nn.init.uniform_(self.pe, -0.02, 0.02)<br><br>def forward(self, X, index):<br>if index is None:<br>pe = self.pe[:X.size(1), :].unsqueeze(0)<br>else:<br>pe = self.pe[index].unsqueeze(0)<br>X = X + pe<br>X = self.dropout(X)<br>return X<br>class PositionalEncoding(nn.Module):<br>def __init__(self, hidden_dim, dropout=0.1):<br>super().__init__()<br>self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)<br>def forward(self, input, index=None, abs_idx=None):<br>B, N, L_P, d = input.shape<br># temporal embedding<br>input = self.tem_pe(input.view(B*N, L_P, d), index=index)<br>input = input.view(B, N, L_P, d)<br># absolute positional embedding<br>return input
Transformer 區塊
論文使用了4層Transformer ,比電腦視覺和自然語言處理任務中常見的數量低。這裡所使用的Transformer 是最基本的也是在原始論文中提到的結構,如下圖4所示:

class TransformerLayers(nn.Module):<br>def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):<br>super().__init__()<br>self.d_model = hidden_dim<br>encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)<br>self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)<br>def forward(self, src):<br>B, N, L, D = src.shape<br>src = src * math.sqrt(self.d_model)<br>src = src.view(B*N, L, D)<br>src = src.transpose(0, 1)<br>output = self.transformer_encoder(src, mask=None)<br>output = output.transpose(0, 1).view(B, N, L, D)<br>return output
3、解碼

此解碼器包含一系列Transformer區塊。它適用於所有的patch(相比之下MAE是沒有位置嵌入,因為他的patch已經有位置資訊),並且層數只有一層,然後使用了簡單的MLP,這使得輸出長度等於每個patch的長度。
4、重建目標

對每一個資料點(i)進行遮蔽patch的計算,並選擇mae (Mean-Absolute-Error)作為主序列和重建序列的損失函數。

這就是整體的架構了

#下面是程式碼實作:
def trunc_normal_(tensor, mean=0., std=1.):<br>__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)<br>def unshuffle(shuffled_tokens):<br>dic = {}<br>for k, v, in enumerate(shuffled_tokens):<br>dic[v] = k<br>unshuffle_index = []<br>for i in range(len(shuffled_tokens)):<br>unshuffle_index.append(dic[i])<br>return unshuffle_index<br>class TSFormer(nn.Module):<br>def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):<br>super().__init__()<br>self.patch_size = patch_size<br>self.seleted_feature = selected_feature<br>self.mode = mode<br>self.spectral = spectral<br>self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)<br>self.pe = PositionalEncoding(out_channel, dropout=dropout)<br>self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)<br>self.encoder = TransformerLayers(out_channel, L)<br>self.decoder = TransformerLayers(out_channel, 1)<br>self.encoder_2_decoder = nn.Linear(out_channel, out_channel)<br>self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))<br>trunc_normal_(self.mask_token, std=.02)<br>if self.spectral:<br>self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)<br>else:<br>self.output_layer = nn.Linear(out_channel, patch_size)<br>def _forward_pretrain(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br><br># mask tokens<br>unmasked_token_index, masked_token_index = self.mask()<br>encoder_input = patches[:, :, unmasked_token_index, :] <br># encoder<br>H = self.encoder(encoder_input) <br># encoder to decoder<br>H = self.encoder_2_decoder(H)<br># decoder<br># H_unmasked = self.pe(H, index=unmasked_token_index)<br>H_unmasked = H<br>H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)<br>H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d<br>H = self.decoder(H_full)<br># output layer<br>if self.spectral:<br># output = H<br>spec_feat_H_ = self.output_layer(H)<br>real = spec_feat_H_[..., :int(self.patch_size/2+1)]<br>imag = spec_feat_H_[..., int(self.patch_size/2+1):]<br>spec_feat_H = torch.complex(real, imag)<br>out_full = torch.fft.irfft(spec_feat_H)<br>else:<br>out_full = self.output_layer(H)<br># prepare loss<br>B, N, _, _ = out_full.shape <br>out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]<br>out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)<br>label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P<br>label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()<br>label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)<br># prepare plot<br>## note that the output_full and label_full are not aligned. The out_full in shuffled<br>### therefore, unshuffle for plot<br>unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)<br>out_full_unshuffled = out_full[:, :, unshuffled_index, :]<br>plot_args = {}<br>plot_args['out_full_unshuffled'] = out_full_unshuffled<br>plot_args['label_full'] = label_full<br>plot_args['unmasked_token_index'] = unmasked_token_index<br>plot_args['masked_token_index'] = masked_token_index<br>return out_masked_tokens, label_masked_tokens, plot_args<br>def _forward_backend(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br>encoder_input = patches # no mask when running the backend.<br># encoder<br>H = self.encoder(encoder_input) <br>return H<br>def forward(self, input_data):<br><br>if self.mode == 'Pretrain':<br>return self._forward_pretrain(input_data)<br>else:<br>return self._forward_backend(input_data)
看完這篇論文,我發現這基本上可以說是複製了MAE,或者說是時間序列的MAE,在預測階段也是與MAE類似,使用編碼器的輸出作為特徵,為下游任務提供特徵數據作為輸入,有興趣的可以讀讀原始論文並且看看論文給的代碼。
以上是五個時間序列預測的深度學習模型比較總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM
讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM科學家已經廣泛研究了人類和更簡單的神經網絡(如秀麗隱桿線蟲中的神經網絡),以了解其功能。 但是,出現了一個關鍵問題:我們如何使自己的神經網絡與新穎的AI一起有效地工作
 新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AM
新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AMGoogle的雙子座高級:新的訂閱層即將到來 目前,訪問Gemini Advanced需要$ 19.99/月Google One AI高級計劃。 但是,Android Authority報告暗示了即將發生的變化。 最新的Google P中的代碼
 數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM
數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM儘管圍繞高級AI功能炒作,但企業AI部署中潛伏的巨大挑戰:數據處理瓶頸。首席執行官慶祝AI的進步時,工程師努力應對緩慢的查詢時間,管道超載,一個
 Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM處理文檔不再只是在您的AI項目中打開文件,而是將混亂變成清晰度。諸如PDF,PowerPoints和Word之類的文檔以各種形狀和大小淹沒了我們的工作流程。檢索結構化
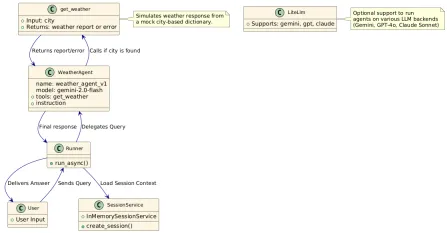 如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM
如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM利用Google的代理開發套件(ADK)的力量創建具有現實世界功能的智能代理!該教程通過使用ADK來構建對話代理,並支持Gemini和GPT等各種語言模型。 w
 在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM
在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM摘要: 小型語言模型 (SLM) 專為效率而設計。在資源匱乏、實時性和隱私敏感的環境中,它們比大型語言模型 (LLM) 更勝一籌。 最適合專注型任務,尤其是在領域特異性、控制性和可解釋性比通用知識或創造力更重要的情況下。 SLM 並非 LLMs 的替代品,但在精度、速度和成本效益至關重要時,它們是理想之選。 技術幫助我們用更少的資源取得更多成就。它一直是推動者,而非驅動者。從蒸汽機時代到互聯網泡沫時期,技術的威力在於它幫助我們解決問題的程度。人工智能 (AI) 以及最近的生成式 AI 也不例
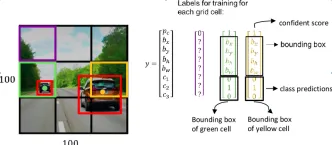 如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM
如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM利用Google雙子座的力量用於計算機視覺:綜合指南 領先的AI聊天機器人Google Gemini擴展了其功能,超越了對話,以涵蓋強大的計算機視覺功能。 本指南詳細說明瞭如何利用
 Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM2025年的AI景觀正在充滿活力,而Google的Gemini 2.0 Flash和Openai的O4-Mini的到來。 這些尖端的車型分開了幾週,具有可比的高級功能和令人印象深刻的基準分數。這個深入的比較


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

SublimeText3 Linux新版
SublimeText3 Linux最新版

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),






