
漸近性質是指隨著資料量增加,演算法的效能是否會趨於穩定或收斂到一定的界限。在機器學習問題中,漸近性質是評估演算法可擴展性和效率的重要指標。了解演算法的漸近性質有助於我們選擇適合的演算法來解決機器學習問題。透過分析演算法在不同資料量下的表現,我們可以預測演算法在大規模資料集上的效率和效能。這對於處理大規模資料集的實際問題非常重要。因此,了解演算法的漸近性質可以幫助我們在實際應用中做出更明智的決策。
常見的機器學習演算法有多種,如支援向量機、樸素貝葉斯、決策樹和神經網路。每個演算法都有自己的優缺點,因此在選擇時需考慮因素如資料量、資料類型和計算資源等。
對於大規模資料集,演算法的時間複雜度是一個重要的考慮因素。如果演算法的時間複雜度很高,處理大規模資料集會非常耗時,甚至不可行。因此,了解演算法的漸近性質至關重要,以選擇一個時間效率高的演算法來解決問題。我們可以透過分析演算法的時間複雜度來確定其漸近性質。時間複雜度描述了演算法的運行時間與輸入規模的成長之間的關係。常見的時間複雜度包括常數時間複雜度O(1),線性時間複雜度O(n),對數時間複雜度O(log n),平方時間複雜度O(n^2)等。在選擇演算法時,我們應該盡量選擇時間複雜度較低的演算法,以提高演算法的效率。當然,除了時間複
以支援向量機為例,演算法的時間複雜度為O(n^3),其中n是訓練資料集的大小。這意味著,隨著訓練資料集的增加,演算法的計算時間會呈現指數級增長。因此,支援向量機在處理大規模資料集時可能會遇到效能瓶頸。相較之下,樸素貝葉斯演算法的時間複雜度是O(n),因此在處理大規模資料集時更有效率。因此,當面臨大規模資料集的情況時,選擇樸素貝葉斯演算法可能會更加合適,因為它能夠在相對較短的時間內完成訓練和預測任務。
空間複雜度也是一個重要的指標,尤其對於記憶體受限的系統。在這種情況下,演算法的空間複雜度可能成為限制因素。舉例來說,神經網路演算法的空間複雜度通常很高,因為它需要儲存大量的權重和神經元狀態。 為了確保演算法的可擴展性和效率,在記憶體受限的情況下,我們可能需要選擇其他演算法或採取一些最佳化措施來減少記憶體使用量。這可以包括使用更節省空間的資料結構、減少不必要的資料複製或快取等。透過這些措施,我們能夠降低演算法的空間複雜度,提升系統的效能。 因此,除了考慮時間複雜度外,空間複雜度也是評估演算法優劣的重要因素之一。在設計和選擇演算法時,我們需要綜合考慮時間複雜度和空間複雜度,以找到最優的解決方案。
此外,演算法的收斂速度也是一個重要的考慮因素。在訓練過程中,我們希望演算法能夠盡快收斂到最優解,以減少訓練時間和計算資源的消耗。因此,了解演算法的收斂速度和收斂性質可以幫助我們選擇一個更有效率的演算法來解決機器學習問題。
總之,漸近性質在機器學習問題中具有重要的意義。透過了解演算法的時間複雜度、空間複雜度、收斂速度和收斂性質等漸近性質,我們可以選擇一個更有效率、可擴展和穩定的演算法來解決機器學習問題。
以上是機器學習問題中漸進性的重要性的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 如何成為統計學家?Apr 15, 2025 am 09:15 AM
如何成為統計學家?Apr 15, 2025 am 09:15 AM介紹 想像一下,有能力在醫療保健,金融或體育等領域為自己和您的公司做出明智的決定。那就是統計學家的角色。 隨著組織中數據的越來越多,對統計學家的需求
 AI如何工作? - 分析VidhyaApr 15, 2025 am 09:14 AM
AI如何工作? - 分析VidhyaApr 15, 2025 am 09:14 AM人工智能:綜合指南 技術使我們能夠設想一個世界,即機器了解我們的偏好,預測我們的需求,並從過去的互動中學習以提供更好的結果。這不是科幻小說;它是
 什麼是像形圖? - 分析VidhyaApr 15, 2025 am 09:09 AM
什麼是像形圖? - 分析VidhyaApr 15, 2025 am 09:09 AM介紹 在數據分析的世界中,有效的溝通是關鍵。 象形圖提供了一個強大的解決方案,以視覺上吸引人且易於消化的格式提供信息。與復雜的圖表和數字不同,象形文字 - 也
 Llama-3.1-STORM-8B:8B LLM優於元和愛馬仕Apr 15, 2025 am 09:08 AM
Llama-3.1-STORM-8B:8B LLM優於元和愛馬仕Apr 15, 2025 am 09:08 AMLlama 3.1風暴8b:有效語言模型的突破 追求高效,準確的語言模型導致了Llama 3.1 Storm 8b的發展,這是80億個參數模型類別的顯著進步。 這是完善的
 如何安裝git? - 分析VidhyaApr 15, 2025 am 09:07 AM
如何安裝git? - 分析VidhyaApr 15, 2025 am 09:07 AMgit:您的版本控制與協作的基本指南 Git是開發人員的關鍵工具,簡化了項目協作和版本控制。 本指南提供了在Linux,MacOS和Wind上安裝GIT的直接說明
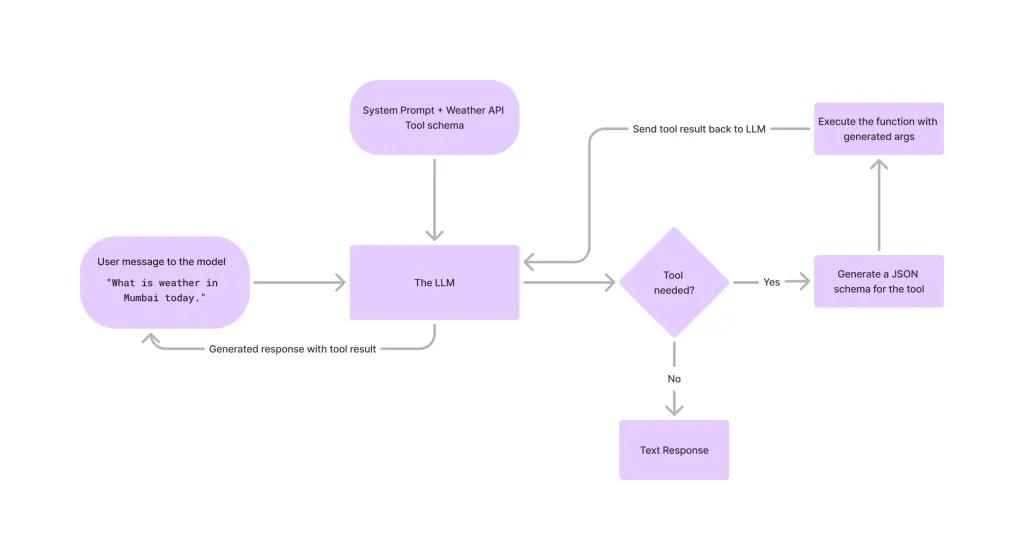 在LLMS中調用工具Apr 14, 2025 am 11:28 AM
在LLMS中調用工具Apr 14, 2025 am 11:28 AM大型語言模型(LLMS)的流行激增,工具稱呼功能極大地擴展了其功能,而不是簡單的文本生成。 現在,LLM可以處理複雜的自動化任務,例如Dynamic UI創建和自主a
 多動症遊戲,健康工具和AI聊天機器人如何改變全球健康Apr 14, 2025 am 11:27 AM
多動症遊戲,健康工具和AI聊天機器人如何改變全球健康Apr 14, 2025 am 11:27 AM視頻遊戲可以緩解焦慮,建立焦點或支持多動症的孩子嗎? 隨著醫療保健在全球範圍內挑戰,尤其是在青年中的挑戰,創新者正在轉向一種不太可能的工具:視頻遊戲。現在是世界上最大的娛樂印度河之一
 沒有關於AI的投入:獲勝者,失敗者和機遇Apr 14, 2025 am 11:25 AM
沒有關於AI的投入:獲勝者,失敗者和機遇Apr 14, 2025 am 11:25 AM“歷史表明,儘管技術進步推動了經濟增長,但它並不能自行確保公平的收入分配或促進包容性人類發展,”烏托德秘書長Rebeca Grynspan在序言中寫道。


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

Dreamweaver CS6
視覺化網頁開發工具

Safe Exam Browser
Safe Exam Browser是一個安全的瀏覽器環境,安全地進行線上考試。該軟體將任何電腦變成一個安全的工作站。它控制對任何實用工具的訪問,並防止學生使用未經授權的資源。

SublimeText3 Linux新版
SublimeText3 Linux最新版

MantisBT
Mantis是一個易於部署的基於Web的缺陷追蹤工具,用於幫助產品缺陷追蹤。它需要PHP、MySQL和一個Web伺服器。請查看我們的演示和託管服務。

WebStorm Mac版
好用的JavaScript開發工具





