Transformer 難道注定無法解決「訓練資料」以外的新問題?
說起大語言模型所展示的令人印象深刻的能力,其中之一就是透過提供上下文中的樣本,要求模型根據最終提供的輸入生成一個響應,從而實現少樣本學習的能力。這一點依靠的是底層機器學習技術「Transformer 模型」,它們也能在語言以外的領域執行上下文學習任務。
根據過去的經驗,已經證明對於在預訓練的混合體中得到充分體現的任務族或函數類來說,選擇適當的函數類進行上下文學習幾乎沒有成本。因此,有些研究人員認為Transformer能夠很好地泛化與訓練資料相同分佈的任務或函數。然而,一個普遍存在但未解決的問題是:在與訓練資料分佈不一致的樣本上,這些模型的表現如何?
在最近的一項研究中,來自 DeepMind 的研究者藉助實證研究,對這個問題進行了探討。他們將泛化問題解釋為以下內容:「一個模型能否利用不屬於預訓練資料混合體中任何基本函數類別的函數的上下文樣本產生良好的預測?(Can a model generate good predictions with in-context examples from a function not in any of the base function classes seen in the pretraining data mixture? )”
這篇內容的重點是探討預訓練過程中使用的資料對由此產生的Transformer模型的少樣本學習能力的影響。為了解決這個問題,研究者首先研究了Transformer在預訓練過程中選擇不同函數類族進行模型選擇的能力(第3節),然後回答了幾個重點案例的OOD泛化問題(第4節)

論文連結:https://arxiv.org/pdf/2311.00871.pdf
在他們的研究中發現了以下情況:首先,預訓練的Transformer在預測從預訓練函數類別中提取的函數的凸組合時非常困難;其次,雖然Transformer可以有效地泛化函數類空間中較為罕見的部分,但當任務超出其分佈範圍時,Transformer仍然會發生錯誤
Transformer無法泛化出預訓練資料以外的認知,因此也無法解決認知以外的問題

總的來說,本文的貢獻如下所述:
使用多種不同函數類別的混合體對Transformer 模型進行預訓練,以便進行上下文學習,並描述了模型選擇行為的特徵;
對於與預訓練資料中函數類別「不一致」的函數,研究了預訓練Transformer 模型在上下文學習方面的行為
強有力的證據已經表明,模型在上下文學習過程中可以在預訓練的函數類中進行模型選擇,而幾乎不需要額外的統計成本,但也存在有限證據,表明模型的上下文學習行為能夠超出其預訓練資料的範圍。
這位研究者認為,這可能是對安全方面來說的一個好消息,至少模型不會隨心所欲地行事

但也有人指出,這篇論文所使用的模型不太合適——「GPT-2 規模」意味著本文模型大概是15 億參數作用,這確實很難泛化。 

接下來,我們先來看看論文細節。
模型選擇現象
在對不同函數類別的資料混合體進行預訓練時,會面臨一個問題:當模型遇到預訓練混合體所支持的上下文樣本時,如何在不同函數類別之間做出選擇?
在研究中發現,當模型接觸到與預訓練資料中的函數類別相關的上下文樣本時,它能夠做出最佳(或接近最佳)的預測。研究人員也觀察了模型在不屬於任何單一成分函數類別的函數上的表現,並在第四部分討論了與預訓練資料完全不相關的函數
首先,我們從線性函數的研究入手,可以看到線性函數在情境學習領域引起了廣泛的關注。去年,史丹佛大學的 Percy Liang 等人發表的論文《變壓器在上下文中能學到什麼?一個簡單函數類別的案例研究》表明,預先訓練的變壓器在學習新的線性函數上下文時表現非常出色,幾乎達到了最佳水平
他們特別考慮了兩個模型:一個是在密集線性函數(線性模型的所有係數都非零)上訓練的模型,另一個是在稀疏線性函數(20 個係數中只有2 個係數非零)上訓練的模型。在新的密集線性函數和稀疏線性函數上,每個模型的表現分別與線性迴歸和 Lasso 迴歸相當。此外,研究者還將這兩個模型與在稀疏線性函數和密集線性函數的混合體上預先訓練的模型進行了比較。

如圖 1 所示,該模型在一個 混合體在情境學習中的表現與只對一個函數類別進行預訓練的模型相似。由於混合體預訓練模型的表現與 Garg et al.[4] 的理論最優模型相似,研究者推論模型也接近最適。圖 2 中的 ICL 學習曲線表明,這種情境模型選擇能力與所提供的上下文範例數量相對一致。在圖 2 中也可以看到,對於特定函數類,使用各種 non-trivial 權重
混合體在情境學習中的表現與只對一個函數類別進行預訓練的模型相似。由於混合體預訓練模型的表現與 Garg et al.[4] 的理論最優模型相似,研究者推論模型也接近最適。圖 2 中的 ICL 學習曲線表明,這種情境模型選擇能力與所提供的上下文範例數量相對一致。在圖 2 中也可以看到,對於特定函數類,使用各種 non-trivial 權重 。
。
ICL學習曲線與最佳基線樣本複雜度幾乎一致。偏差很小,隨著ICL樣本數量的增加,偏差迅速減小,與圖1中的ICL學習曲線上的點相符
圖2顯示,Transformer模型的ICL泛化會受到分佈外的影響。雖然密集線性類別和稀疏線性類別都是線性函數,但可以看到圖2a中紅色曲線(對應於只在稀疏線性函數上進行預訓練並在密集線性資料上進行評估的Transformer)的表現很差,反之亦然,圖2b中茶色曲線的表現也很差。研究者在其他非線性函數類別中也觀察到了類似的表現

回到圖1 的實驗,將誤差繪製為整個可能範圍內非零係數數量的函數,結果顯示,在w = .5 的混合體上預處理的模型, ,在整個過程中的表現與在混合體上預處理的模型(即w = 0 以及w = 1)一樣好(圖3a)。這表明該模型能夠進行模型選擇,以選擇是否僅使用預訓練混合體中一個基函數類的知識或另一個基函數類的知識進行預測。
,在整個過程中的表現與在混合體上預處理的模型(即w = 0 以及w = 1)一樣好(圖3a)。這表明該模型能夠進行模型選擇,以選擇是否僅使用預訓練混合體中一個基函數類的知識或另一個基函數類的知識進行預測。
事實上,圖3b 顯示,當上下文中提供的樣本來自非常稀疏或非常密集的函數時,預測結果幾乎與只使用稀疏資料或只使用密集資料預訓練的模型預測結果完全相同。然而,在兩者之間,當非零係數的數量≈4 時,混合預測結果偏離了純密集或純稀疏預訓練 Transformer 的預測結果。
這表明對混合體進行預訓練的模型並不是簡單地選擇單一函數類別進行預測,而是預測介於兩者之間的結果。
模型選擇能力的限制
接著,研究人員從兩個角度檢視了模型的ICL泛化能力。第一,測試了模型在訓練過程中未曾接觸過的函數的ICL表現;第二,評估了模型在預訓練中曾經接觸過的函數的極端版本的ICL表現
在這兩種情況下,研究幾乎沒有發現分佈外泛化的證據。當函數與預訓練期間看到的函數相差很大時,預測就會不穩定;當函數足夠接近預訓練資料時,模型可以很好地近似

Transformer在中等稀疏等級(nnz = 3到7)下的預測與預訓練提供的任何函數類別的預測都不相似,而是介於兩者之間,如圖3a所示。因此,我們可以推斷模型具有某種歸納偏差,使其能夠以非平凡的方式組合預先訓練的函數類別。例如,我們可以懷疑模型可以根據預訓練期間看到的函數組合來產生預測。為了驗證這個假設,研究者探討了對線性函數、正弦曲線和兩者的凸組合執行ICL的能力。他們將重點放在一維情況上,以便更容易評估和可視化非線性函數類別
圖4 顯示,雖然在線性函數和正弦曲線的混合上預訓練的模型(即 )能夠分別對這兩個函數中的任何一個做出良好的預測,它無法擬合兩者的凸組合函數。這表明圖 3b 中所示的線性函數插值現象並不是 Transformer 上下文學習的可概括的歸納偏差。然而,它繼續支持更狹隘的假設,即當情境樣本接近預訓練中學習的函數類別時,模型能夠選擇最佳函數類別用於預測。
)能夠分別對這兩個函數中的任何一個做出良好的預測,它無法擬合兩者的凸組合函數。這表明圖 3b 中所示的線性函數插值現象並不是 Transformer 上下文學習的可概括的歸納偏差。然而,它繼續支持更狹隘的假設,即當情境樣本接近預訓練中學習的函數類別時,模型能夠選擇最佳函數類別用於預測。

如需了解更多研究細節,請查閱原文
以上是DeepMind指出「Transformer無法超出預訓練資料實現泛化」,但有人投來質疑的詳細內容。更多資訊請關注PHP中文網其他相關文章!
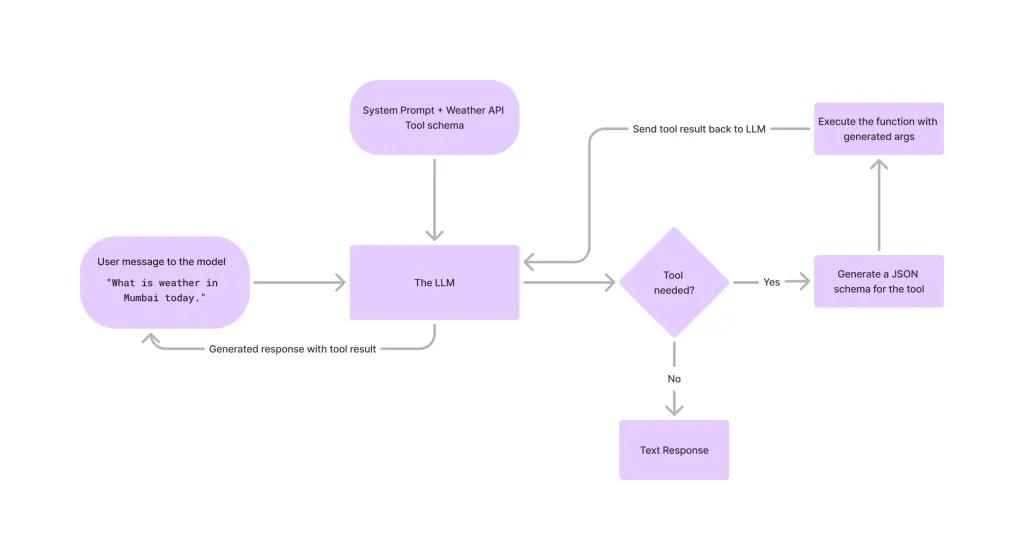 在LLMS中調用工具Apr 14, 2025 am 11:28 AM
在LLMS中調用工具Apr 14, 2025 am 11:28 AM大型語言模型(LLMS)的流行激增,工具稱呼功能極大地擴展了其功能,而不是簡單的文本生成。 現在,LLM可以處理複雜的自動化任務,例如Dynamic UI創建和自主a
 多動症遊戲,健康工具和AI聊天機器人如何改變全球健康Apr 14, 2025 am 11:27 AM
多動症遊戲,健康工具和AI聊天機器人如何改變全球健康Apr 14, 2025 am 11:27 AM視頻遊戲可以緩解焦慮,建立焦點或支持多動症的孩子嗎? 隨著醫療保健在全球範圍內挑戰,尤其是在青年中的挑戰,創新者正在轉向一種不太可能的工具:視頻遊戲。現在是世界上最大的娛樂印度河之一
 沒有關於AI的投入:獲勝者,失敗者和機遇Apr 14, 2025 am 11:25 AM
沒有關於AI的投入:獲勝者,失敗者和機遇Apr 14, 2025 am 11:25 AM“歷史表明,儘管技術進步推動了經濟增長,但它並不能自行確保公平的收入分配或促進包容性人類發展,”烏托德秘書長Rebeca Grynspan在序言中寫道。
 通過生成AI學習談判技巧Apr 14, 2025 am 11:23 AM
通過生成AI學習談判技巧Apr 14, 2025 am 11:23 AM易於使用,使用生成的AI作為您的談判導師和陪練夥伴。 讓我們來談談。 對創新AI突破的這種分析是我正在進行的《福布斯》列的最新覆蓋範圍的一部分,包括識別和解釋
 泰德(Ted)從Openai,Google,Meta透露出庭,與我自己自拍Apr 14, 2025 am 11:22 AM
泰德(Ted)從Openai,Google,Meta透露出庭,與我自己自拍Apr 14, 2025 am 11:22 AM在溫哥華舉行的TED2025會議昨天在4月11日舉行了第36版。它的特色是來自60多個國家 /地區的80個發言人,包括Sam Altman,Eric Schmidt和Palmer Luckey。泰德(Ted)的主題“人類重新構想”是量身定制的
 約瑟夫·斯蒂格利茲(Joseph StiglitzApr 14, 2025 am 11:21 AM
約瑟夫·斯蒂格利茲(Joseph StiglitzApr 14, 2025 am 11:21 AM約瑟夫·斯蒂格利茨(Joseph Stiglitz)是2001年著名的經濟學家,是諾貝爾經濟獎的獲得者。斯蒂格利茨認為,AI可能會使現有的不平等和合併權力惡化,並在一些主導公司手中加劇,最終破壞了經濟上的經濟。
 什麼是圖形數據庫?Apr 14, 2025 am 11:19 AM
什麼是圖形數據庫?Apr 14, 2025 am 11:19 AM圖數據庫:通過關係徹底改變數據管理 隨著數據的擴展及其特徵在各個字段中的發展,圖形數據庫正在作為管理互連數據的變革解決方案的出現。與傳統不同
 LLM路由:策略,技術和Python實施Apr 14, 2025 am 11:14 AM
LLM路由:策略,技術和Python實施Apr 14, 2025 am 11:14 AM大型語言模型(LLM)路由:通過智能任務分配優化性能 LLM的快速發展的景觀呈現出各種各樣的模型,每個模型都具有獨特的優勢和劣勢。 有些在創意內容gen上表現出色


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

SublimeText3 Linux新版
SublimeText3 Linux最新版

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

Dreamweaver CS6
視覺化網頁開發工具





