70年AI发展迎来大一统？马毅、曹颖、沈向洋最新AI综述：探索智能发生的基本原则与「标准模型」

​人工智能发展七十年，虽然技术指标上不断刷新，但到底什么是「智能」，它如何出现及发展的，还没有答案。

最近马毅教授联手计算机科学家沈向洋博士、神经科学家曹颖教授发表了一篇对智能出现及发展的研究综述，希望将智能体的研究在理论上统一起来，增进对人工智能模型的理解与可解释性。

论文链接：http://arxiv.org/abs/2207.04630

文中引入了两个基本原则：简约（Parsimony）与自洽（ Self-consistency）。

作者认为这是智力、人工或自然的兴起的基石。尽管在经典文献里，对这两个原则各自的相关论述、阐述众多，但本文对这两个原则以完全可度量和可计算的方式重新进行解读。

基于这两个第一性的原则，作者推演出了一个高效的计算框架：压缩闭环转录，该框架统一并解释了现代深度网络和许多人工智能实践的演变。

两大基本原则：简约与自洽

在深度学习加持下，过去十年人工智能取得的进展主要依赖于训练同质化的黑箱模型，使用粗暴的工程方法训练大规模神经网络。

虽然性能提高了，也无需手动设计特征，但神经网络内部学到的特征表示却是不可解释的，并且大模型带来其他的难题，比如不断提高的数据收集和计算的成本、学到的表征缺乏丰富性、稳定性（模式崩溃）、适应性（容易出现灾难性遗忘）；对变形或对抗性攻击缺乏稳健性等。

作者认为，目前在深度网络和人工智能的实践中出现这些问题的根本原因之一是对智能系统的功能和组织原则缺乏系统和综合的理解。

举个例子，训练用于分类的判别式模型和用于采样或重放的生成性模型基本上在实践中是分开的。这样训练的模型通常叫开环系统，需要通过监督或自监督进行端到端的训练。

在控制理论中，这种开环系统（open-loop systems）不能自动纠正预测中的错误，而且对环境的变化没有适应性；正是因为这样的问题，在控制系统（controlled systems）中大家广泛采用「闭环反馈」，使系统能够自主纠正错误。

类似的经验在学习中也适用：一旦判别式模型和生成性模型结合在一起，形成一个完整的闭环系统，学习就可以变得自主（无需外部监督），而且更有效率、更稳定、更有适应性。

为了理解智能系统中可能需要的功能组件，如判别器或生成器等部件，我们需要从一个更加「原则」和「统一」的角度来理解智能。

文中提出两个基本原则：简约（Parsimony）和自洽（Self-consistency），分别回答了关于学习的两个基本问题。

• 学什么：要从数据中学习什么，如何衡量学到的好坏？

• 怎么学：我们如何通过高效和有效的计算框架来实现这样一个学习的目标？

对于第一个「学什么」的问题，简约原则认为：​

智能系统的学习目标就是从外部世界的观测数据中找出低维的结构，并且以最紧凑和结构化的方式重新组织和表示它们。

这也就是「奥卡姆剃刀」原则：如无必要，勿增实体。

如果沒有這原則，智能就不可能發生與存在！如果對外在世界的觀測資料沒有低維度結構，就沒有什麼值得學習或記憶的東西，也就無法進行良好的泛化或預測。

而且智慧系統需要盡量節省資源，如能量、空間、時間和物質等，在某些情況下，該原則也被稱為「壓縮原則」。但是，智慧的簡約性（Parsimony of Intelligence）並不是要實現最好的壓縮，而是要透過高效的計算手段來獲得觀測資料最緊湊且結構化的表達。

那麼簡約性該如何度量呢？

對於一般的高維度模型來說，許多常用的數學或統計「測量」的計算成本都是指數級的，或者對於有低維度結構的資料分佈來說，甚至是沒有定義的，例如最大似然、KL分歧、互資訊、Jensen-Shannon和Wasserstein距離等。

作者認為學習的目的其實就是建立一個映射（通常是非線性的），從原始高維輸入得到一個低維的表示。

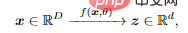
這樣，得到的特徵z的分佈應該更加緊湊和結構化；緊湊意味著儲存上更經濟；結構化意味著存取和使用更有效率：特別是線性結構，是內插或外推的理想選擇。

為了這個目的，作者引入了線性判別表示（LDR），實現三個子目標：

1. 壓縮：將高維感官資料x映射到低維表徵z；
2. 線性化：將分佈在非線性子麵的每一類物體映射到線性子空間；
3. #稀疏化：將不同類別對應到相互獨立或最不相關的子空間。

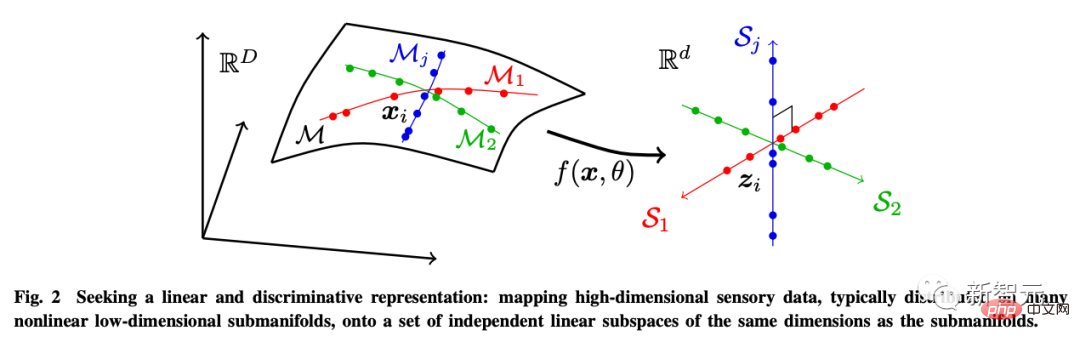
而這幾個目標可以透過最大編碼率減少（rate reduction）來實現，保證所學到的LDR模型具有最優的簡約性能。

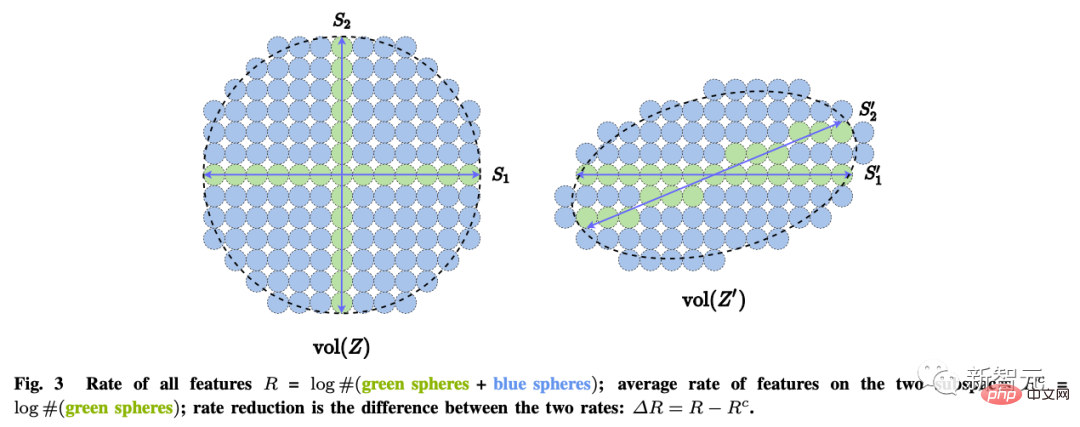
#對於第二個「怎麼學」的問題，自洽原則認為：

一個自主的智慧系統透過最小化觀測到的資料和再產生的資料在內部表達中的差異，為外部世界的觀測尋求一個最自洽的模型。

只是簡約原則並不能確保學到的模型能夠捕捉到關於外在世界的資料中的所有重要資訊。例如，透過最小化交叉熵，將每個類別映射到一個一維的one-hot向量，可以被視為簡約性的一種形式。

它可能會學到一個好的分類器，但學到的特徵也可能會崩潰成一個singleton，也稱為神經崩潰。這樣學到的特徵將不再包含足夠的資訊來重新產生原始資料。

即使我們考慮更普遍的LDR模型，僅靠最大化編碼率差也無法自動確定環境特徵空間的正確維度。

如果特徵空間的維度太低，學到的模型就會與資料不符；如果太高，模型可能會過度匹配。

更一般地說，我們認為知覺的學習不同於學習具體任務。感知的目標是學習關於所感知的一切可預測的內容。

就像愛因斯坦所說過的：「事情應該力求簡單，不過不能過於簡單。」

通用學習引擎

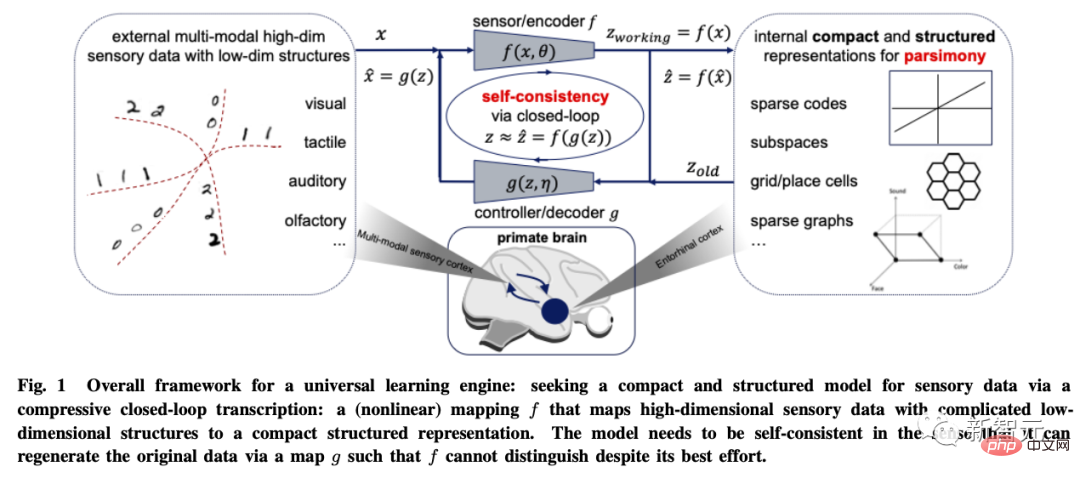
基於這兩個原則，文章以視覺影像資料建模為例推導出了壓縮閉環轉錄框架（compressive closed-loop transcription framework）。

其透過比較和最小化內部表徵的差異，在內部對非線性資料子流型進行壓縮式閉環轉錄，以實現LDR。

編碼器/感測器和解碼器/控制器之間的追逃遊戲，可以讓解碼表徵產生的資料的分佈追逐和匹配觀察到的真實資料分佈。

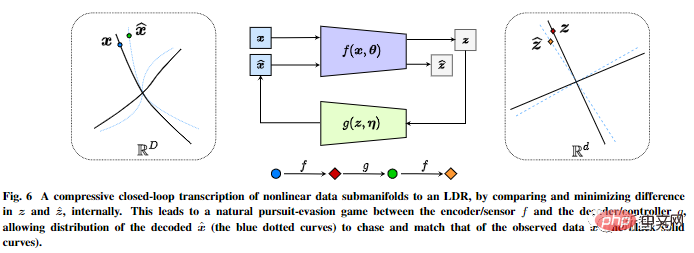
另外作者指出，壓縮式閉迴路轉錄可以有效地進行增量學習。

一個新的資料類別的LDR模型可以透過編碼器和解碼器之間的一個有約束的博弈來學習的：過去學習到的類別的記憶可以很自然地作為博弈中的約束被保留，也就是作為閉環轉錄的「固定點」。

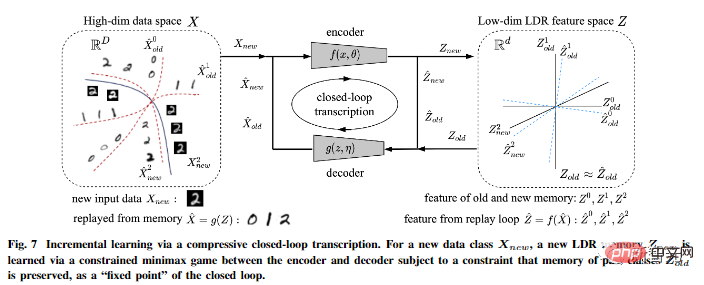
文中也對這個框架的普適性提出了更多的推測性想法，將其擴展到三維視覺和強化學習，並預測其對神經科學、數學和高級智慧的影響。

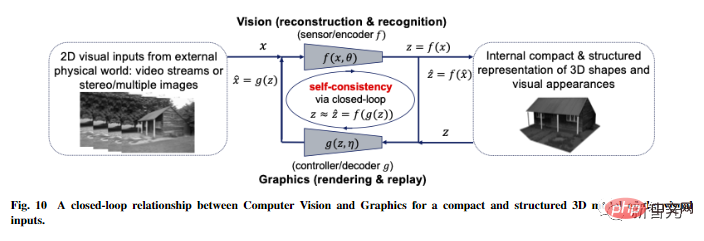
透過這個由第一原理推導出來的框架：資訊編碼理論、閉環回饋控制、最佳化/深度網路和博弈論的概念都有機地整合在一起，成為一個完整的、自主的智慧系統的必要組成部分。

值得一提的是，壓縮閉環式架構在自然界的所有智慧生物以及不同尺度上無所不在：從大腦（壓縮感知資訊），到脊椎迴路（壓縮肌肉運動），直到DNA（壓縮蛋白質的功能資訊）等等。

所以作者認為，壓縮性閉環轉錄應該是所有智慧行為背後的「通用學習引擎」。它使得自然的或人工的智慧系統能夠從看似複雜的感知資料中發現並提煉出低維度的結構，把它們轉換為簡潔規則的內在表達，以利於將來正確地判斷和預測外在世界。

這是一切智慧發生與發展的運算基礎與機制。

參考資料：http://arxiv.org/abs/2207.04630

以上是70年AI发展迎来大一统？马毅、曹颖、沈向洋最新AI综述：探索智能发生的基本原则与「标准模型」的詳細內容。更多資訊請關注PHP中文網其他相關文章！