如何在因果推論中更好地利用數據？

導讀：#這次分享題目為《如何在因果推論中更好地利用資料？ 》，主要介紹團隊近期在因果上已發表論文的相關工作。本報告從兩個方面來介紹我們如何利用更多的數據來做好因果推斷，一個是利用歷史對照數據來明確緩解混淆偏差，另一個是多源數據融合下的因果推斷。

全文目錄：

• #因果推論背景
• 糾偏因果樹GBCT
• 因果資料融合
• 在螞蟻的業務應用

一、因果推斷背景

##常見的機器學習預測問題一般設定在同樣的系統裡面，如通常會假設獨立同分佈，例如預測吸菸的人中得肺癌的機率、圖片分類等預測問題。而因果的問題則關心的是數據背後的機制，常見的問題如“吸煙是否導致肺癌”，類似的問題則為因果的問題。

在因果效應估計問題裡有兩類很重要的數據：一類是觀測數據，另一類則為隨機對照實驗產生的實驗數據。

• 觀測資料是我們實際生活或產品累積下來的資料。例如抽煙的數據，有的人喜歡抽煙，觀察數據則是抽煙者的相關數據，最終抽煙者中的一部分人得癌症。機器學習預測問題就是估計條件機率P（得肺癌｜吸菸），也就是在給定吸菸的條件下，觀察吸菸者得肺癌的機率。在上述的觀測資料中，抽煙的分配其實並不是隨機的：每個人抽煙的偏好不同，同時也會受環境的影響。
• 回答因果問題最好的方式是進行隨機對照實驗。實驗數據是透過隨機對照的實驗得到的。在隨機對照實驗中，treatment 的分配是隨機的。假設需要透過做實驗的方式得到「吸菸是否會導致肺癌」的結論，首先需要找到足夠多的人，強制其中一半人抽煙，同時強制另一半人不抽煙，並觀察兩組人得肺癌的機率。雖然隨機對照試驗在部分場景下受制於道德、政策等因素而不可實現，在部分領域中隨機對照實驗仍可進行，例如在搜推廣中的 A/B test 等。

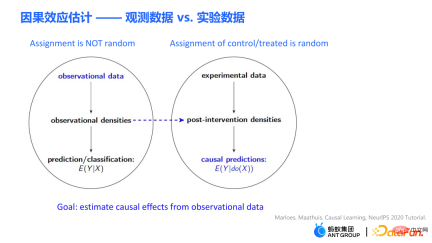
因果估計問題E(Y|do(X)) 問題和傳統的預測或分類問題E(Y|X) 之間的主要區別在於：給定的條件中出現了Judy Pearl 提出的干預表示符號do。透過幹預，強制將 X 變數設定為某個值。本次報告分享中的因果效應估計主要指的是從觀測資料中估計因果效應。

在因果推論中如何更好地利用資料？本次報告將以兩個團隊近期已發表論文為例子去介紹這樣一個主題。 #

• 第一個工作是如何更好地利用歷史對照資料。例如在某個時間點舉行了一個行銷大促的活動，在這個時間點之前的時間稱為“幹預前”，在這個時間點之後的時間稱為“幹預後”。我們希望在介入前就知道採取介入將帶來多少實際的效果，進而輔助我們做下一步決策。在這次行銷活動開始之前，我們擁有使用者的歷史表現數據，第一個工作主要是介紹如何利用好「幹預前」的數據，輔助數據糾偏工作以更好地評估幹預的效果。
• 第二個工作主要是介紹如何更好地利用多來源異質資料。機器學習中也常涉及此類問題，常見的問題如 domain adaptation、transfer learning 等。在今天的報告中，將從因果的視角去考慮多源異質資料的利用問題，即假設在有多個資料來源的情況下，如何更好地估計因果效應。

二、糾偏因果樹GBCT

#1、傳統的因果樹

樹演算法主要由兩個模組組成：

• 分裂準則：根據分割準則將一個節點分裂成兩個子節點
• 參數估計：分裂完成後，例如最終停止分裂，根據參數估計的方法在葉子節點上預測新樣本或群體的因果效應

一些傳統因果樹演算法是根據因果效應的異質性進行分裂的，基本思想是希望分裂之後的左子節點和右子節點的因果效應差異較大，透過分裂捕捉到不同資料分佈的因果效應異質性。

傳統因果樹的分裂準則，例如：

• #uplift tree 的分裂準則為最大化左右子節點的因果效應差異，差異的測量使用歐氏距離、KL 散度等距離測量；
• #causal tree 分裂準則可直觀地解釋為最大化因果效應的平方。可透過數學證明，此分裂準則等價於最大化葉節點因果效應變異數。

常見的參數估計做法是直接在分裂後的葉子節點上將實驗組的平均outcome 減去對照組的平均outcome，以此作為因果效應的估計值。如果是隨機對照實驗，則 treatment 的分配機制是隨機的，由此計算得到的平均差值即為因果效應。隨機分配機制確保實驗組和對照組的資料分佈是相同的，即稱為同質性。

因果樹中分裂得到子節點，可以保證分裂得到的左子節點和右子節點的分佈是同質的嗎？

2、糾偏因果樹GBCT

#傳統的causal tree、uplift tree 並不能保證分裂後的左子節點和右子節點的分佈是同質的。因此上一節提到的傳統估計值是有偏的。

我們的工作著重於去估計實驗組（treatment組）上的平均因果效應 CATT。 CATT 的定義為：

進一步，傳統的因果效果估計值拆分成兩部分：

選擇偏差（selection bias/confounding bias）可定義為：

其直覺意義為在實驗組中treatment=0 時的估計值，減去在對照組中treatment=0 時的估計值。在傳統的因果樹中上述的 bias 是沒有被刻畫的，選擇偏差可能會影響我們的估計，從而導致最終的估計是有偏的。

我們的想法是利用產品或平台上累積的歷史對照數據，從而明確地減少選擇偏差。具體操作是基於兩個假設：

• 假設1：可觀測到介入之前實驗組和對照組在 treatment=0 的狀態下的 outcome 的表現。以金融信貸產品中信用卡產品提額操作為例，在提額之前，我們可觀察到用戶平時的使用表現，即實驗組和對照組在不提額狀態下（treatment=0）的outcome 的表現是可獲得的；
• 假設2：假設outcome 的y 在幹預前後滿足一定的連續性。直觀理解為一個使用者或群體行為的變化在幹預前後不會太劇烈。

具體的做法：

① 分割準則

• 分裂準則的第一部分與傳統因果樹類似，透過擬合歷史資料的outcome# 從而降低經驗損失。例如在不提額狀態下透過函數擬合使用者行為。
• 分裂準則的第二部分是使用混淆熵。混淆熵相對於均方誤差而言，可以捕捉高階資訊。公式：

#的直覺意義是：在實驗組中，使用對照組的模型來估計；在對照組中，使用實驗組的模型進行估計；使這兩部分的估計盡量接近，從而使得實驗組和對照組的分佈盡量接近一致。混淆熵的使用是我們這項工作的主要貢獻之一。

#

• 最終損失為以上兩部分的加權和。注意到損失中主要使用的是乾預前  的數據（經驗損失部分仍會使用乾預後的數據來擬合），即用乾預前的數據進行輔助糾偏。

② 參數估計

• 參數估計使用的是乾預後（t≥τ ）的數據進行因果效應的估計。主要使用乾預前的資料糾偏學習得到一個樹結構，在葉子節點中使用乾預後的資料進行因果效應的估計，由於使用乾預前的資料進行了明確地糾偏，因此在使用乾預後的資料計算得到的估計會更加準確。
• （PPT 的右邊）由右圖所示，黃色的線代表實驗組，藍色的組別代表對照組。業務中的一些策略可能會導致實驗組和對照組的分配不是隨機的，兩者的分佈有明顯的差異。經過GBCT 糾偏後，葉子節點上乾預前的實驗組和對照組的數據分佈基本上是對齊的，從某種意義上達到了類似模擬隨機對照實驗的效果，因此使用乾預後的數據估計因果效應（黃線下的面積減去藍線下的面積）會更準確。

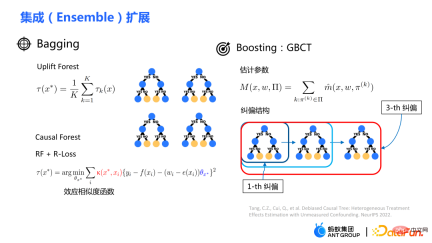
傳統的樹模型的整合包括 bagging、boost 等方法。 uplift forest 或 causal forest 使用的整合方法為 bagging 法，uplift forest 的集合變成直接求和，而causal forest 的整合需要解一個損失函數。

由於在 GBCT 中設計了明確糾偏的模組，從而 GBCT 支援使用 boosting方法進行整合。基本想法與boosting 類似：在第一棵樹糾偏完之後，第二棵樹進行糾偏，第三棵樹進行糾偏……

實驗方面做了兩部分實驗：

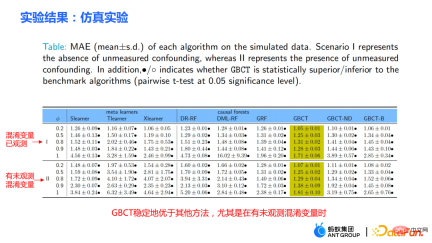
① 模擬實驗。 在含有 ground truth 的模擬實驗下，檢驗 GBCT 的方法是否能夠達到預期的效果。模擬實驗的資料產生分為兩部分（表格中的第一列Φ表示選擇偏倚，Φ值越大，對應的選擇偏差就越強；表格中的數值為MAE，MAE 值越小表示方法越好） ：

• 第一部分是混淆變數已觀測。在混淆變數都已觀測的情況下，檢驗 GBCT 的方法相對於傳統方法是否更穩健。由表中數據可得出結論，選擇偏差越大，傳統方法（meta learner、causal forest 等）表現越差。
• 第二部分是存在未觀測的混淆變數。此時許多傳統方法的效果會顯著變差。對 GBCT 而言，在存在未觀測混淆變數時表現較穩定，同時穩定地比其他方法表現得更好。
• 表格中最後兩列（GBCT-ND, GBCT-B）是消融實驗，也就是去掉一些模組的GBCT 的弱化版本，進而說明我們提出的每個模組都是有用的。

② 真實信用卡提額資料。進行隨機對照的實驗，同時根據隨機對照實驗建構了有偏數據。在不同的設定下，GBCT 方法比傳統的方法穩定地好，尤其是在有偏的數據上，顯著比傳統的方法表現得好。

#

三、因果資料融合

第二個工作是因果資料融合，也就是在擁有多個資料來源的情況下，如何更好地估計因果效應。

主要的符號：是多個資料來源，Y 是outcome，A 是treatment，X 是關注的協變量，Z 是除X 了外每個資料來源（域）的其他協變量，S 是域的indicator用於表示屬於哪個域，μ 是潛在結果的期望值。將outcome拆解成如下表達式：

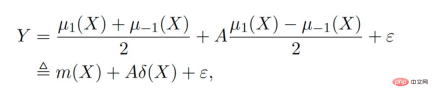
#target function δ 用於估計每個領域上的因果效應，另外nuisance functions 包括主效應、傾向性分數、域傾向性分數、效果的變異數等。

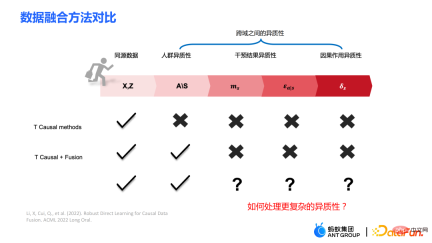
一些傳統的方法，例如meta learner 等都是假設資料是同源的，即分佈是一致的。一些傳統的資料融合方法可以處理在跨域之間人群的異質性，但是無法明確地捕捉到干預結果跨域的異質性以及因果作用跨域的異質性。我們的工作主要是處理更複雜的跨域間的異質性，包括幹預結果跨域之間的異質性以及因果作用跨域之間的異質性。

WMDL 演算法的框架圖如上圖所示。主要的模組為：

• propensity scores
• outcome models
• #causal information-aware weighting module

#三個模組綜合起來就得到了最終的估計。 WMDL 演算法的三個亮點為：

• 如何刻畫不同程度的跨域之間的異質性
• 如何設計weighting 的模組以用上更多的資訊
• 如何得到一個doubly robust 的估計

#在本次工作中不是透過估計實驗組的outcome 和對照組的outcome，然後作差得到因果效應的估計，而是直接估計因果效應，即Direct Learning。 Direct Learning 的好處是可以避免實驗組和控制組中較高頻的噪音訊號。

左邊部分假設了多個領域之間因果效應是一樣的，但其outcome 可能存在異質性；右邊部分假設每個域之間的因果效應不一樣，即在不同的域之間，即使它的協變量一樣，其因果效應也不同。

#

公式是根據拆解式推導得到的，outcome Y 減去 main effect 除以treatment，估計的是 I(X)，得到的最優解即為 δ(X)。 中的分子是後面將要提到的causal information-aware weighting module，是我們本次工作的一個主要貢獻點；分母則類似於doubly robust 方法中的傾向性得分，只不過本次工作中同時考慮了域的資訊。如果不同域之間的因果效應不一樣，會同時考慮域的 indicator 資訊。

本工作三方面的優勢：

#① 透過不同的設計，不僅能處理幹預結果的異質性，同時可以處理因果作用之間的異質性；

② 具有doubly robustness 性質。在論文中給出了證明，只要域的傾向性評分模型或主效應模型兩者之一的估計是無偏的，最終得到的估計就是無偏的（實際情況略複雜一點，細節見論文）；

③ 本次工作主要設計了半參模式框架。其中模型的每一個模組都可以用任何機器學習的模型，甚至可以將整個模型設計進神經網路中，實現端到端的學習。

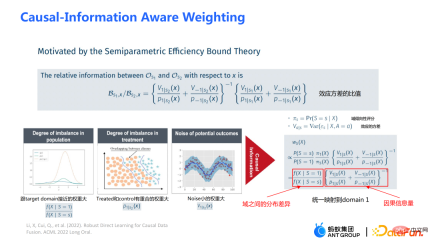
Weighting 的模組是從統計中的 efficiency bound theory 推導出來的。主要包含兩方面資訊：

① #是域之間分佈差異平衡轉換的模組；是因果相關的資訊量模組。可透過左邊三幅圖來輔助理解：如果源域（source domain）和目標域（target domain）之間分佈的差異較大，則優先給與目標域（target domain）較接近的樣本以較大的權重；

② 透過分母上的傾向性評分函數的設計，給實驗組和對照組中存在重疊（overlap）的這部分樣本以較大的權重；

③ 透過V 刻畫資料中的雜訊。由於雜訊在分母上，雜訊小的樣本將得到較大的權重。

透過巧妙地將上述三部分結合在一起，可以將不同域之間的分佈差異以及不同因果資訊的表現映射到統一的域中。

不管在同質的因果效應或異質的因果效應下，WMDL（Weighted Multi-domain Direct Learning ）方法都有較好的效果。右圖則是對 weighting 模組進行了消融實驗，實驗顯示了 weighting 模組的有效性。綜上所述，WMDL 方法穩定地比其他方法效果好，估計的變異數比較小。

四、在螞蟻的業務應用

在金融信貸風控場景中，幹預的手段如提額、降價等，希望得到預期的效果如餘額或風險的變化量。在一些實際的場景中，GBCT 的糾偏工作會利用提額前一段時間內的歷史表現（實驗組和對照組在不提額下的狀態可獲得），透過歷史的資訊進行明確糾偏，使得乾預後的估計會更加準確。 GBCT 分裂到一個子節點，使得介入前行為對齊，則介入後的因果效應就比較容易估計了。 （糾偏後得到的）圖中紅色為提額組，藍色為不提額組，中間的灰色區域即為估計的因果效應。 GBCT 幫助我們更好地做出智慧決策，並控制信貸產品的餘額及風險。

五、問答環節

#Q1：請問 GBCT 糾偏與雙重差分方法（DID）有何異同？

A1：GBCT 糾偏主要想法是利用歷史對照資訊明確地降低選擇偏倚，GBCT 的方法和DID 雙重差分的方法有相似也有不同之處：

• 相似的地方是二者都利用了歷史資訊；
• 不同的地方在於兩者對於歷史資訊的處理方式。 DID 假設歷史資料中的實驗組和對照組之間存在固定常值的間隔（gap），在預測時減去間隔（gap）。由於選擇偏差，實驗組和對照組的分配不是隨機的，GBCT 透過糾偏的方式，將歷史的實驗組和對照組對齊。

Q2：GBCT 在未觀測混淆變數上會表現得更好，有什麼比較直覺的解釋？

A2：如果所有的混淆變數已觀測的話，滿足可忽略性（Ignorability）假設，某種程度上，雖然沒有明確地降低選擇偏倚，實驗組和對照組也有可能透過傳統的方法來對齊，實驗顯示GBCT 的表現要略勝一籌，透過顯式糾偏使得結果更穩定一些。

假設存在一些未觀測到的混淆變量，此類場景在實際中是非常常見的，歷史的對照數據中也存在未觀測到的混淆變量，例如在提額前，家庭狀況、收入的變化等可能觀測不到，但是用戶的金融行為已經透過歷史數據體現出來了。我們希望透過歷史的表現訊息，以混淆熵等方式明確降低選擇偏倚，使得在樹分裂時，將混淆變數之間的異質性刻畫到分裂的子節點中。在子節點中，使得未觀測的混淆變數有更大的機率是比較相近的，因此估計的因果效應相對更準確。

Q3：有將 GBCT 和 Double Machine Learning（DML）做過比較嗎？

A3：做過比較。 Double Machine Learning 是一個半參的方法。我們這篇工作比較著重在 tree-based 方法，所以選用的 base learner 都是一些 tree 或 forest 等相關的方法。表格中的 DML-RF 是 Double Machine Learning 版的 Random Forest。 

相較於 DML，GBCT 主要是在考慮如何利用歷史的對照資料。在比較方法中，會把歷史的 outcome 直接當作協變數處理，但這種處理方法顯然沒有把資訊用得很好。

Q4：業務中可能會遇到的比較相似的問題是，離線可能會有選擇偏差。但是線上的偏差可能會和離線的偏差存在一些偏差。此時在離線做效果評估時，可能沒有辦法非常準確地對離線效果進行估計。

A4：這個問題在金融場景是一個非常本質的問題。在搜推廣中可以透過線上學習或 A/B test 部分克服離線與線上之間的差異。在金融場景，受政策影響無法輕易地在線上做實驗；另外表現的觀測週期通常較長，如信用產品觀察到使用者的回饋需要至少 1 個月的觀測時間。因此實際上很難完美地解決這個問題。

#

我們一般採取如下方式：在離線評估時使用不同時期（OOT）的測試資料去做驗證，觀察其表現的穩健性。如果測驗表現比較穩定的，那麼相對來說更有理由相信其在線上的表現也是不錯的。

#

以上是如何在因果推論中更好地利用數據？的詳細內容。更多資訊請關注PHP中文網其他相關文章！