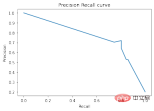
在準確率-召回率曲線上,同樣的點是用不同的座標軸繪製的。警告:左邊的第一個紅點(0%召回率,100%精確度)對應0條規則。左邊的第二個點是第一個規則,等等。
Skope-rules使用樹模型產生規則候選項。首先建立一些決策樹,並將從根節點到內部節點或葉節點的路徑視為規則候選項。然後透過一些預先定義的標準(如精確度和召回率)對這些候選規則進行過濾。只有那些精確度和召回率高於其閾值的才會被保留。最後,應用相似性過濾來選擇具有足夠多樣性的規則。一般情況下,應用Skope-rules來學習每個根本原因的潛在規則。

專案網址:https://github.com/scikit-learn-contrib/skope-rules
- Skope-rules是一個建立在scikit-learn之上的Python機器學習模組,在3條款BSD許可下發布。
- Skope-rules旨在學習邏輯的、可解釋的規則,用於 "界定 "目標類別,即高精度地檢測該類別的實例。
- Skope-rules是決策樹的可解釋性和隨機森林的建模能力之間的一種權衡。

schema
安裝
#可以使用pip 取得最新資源:
pip install skope-rules
快速開始
SkopeRules 可用來描述具有邏輯規則的類別:
from sklearn.datasets import load_iris
from skrules import SkopeRules
#dataset
dataset = load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
clf = SkopeRules(max_depth_duplicatinotallow=2,
clf = SkopeRules(max_depth_duplicatinotallow=2,
clf = SkopeRules(max_depth_duplicatinotallow=2,
n_estimators_##30,_#30,_#. ,
recall_min=0.1,
feature_names=feature_names)
for idx, species in enumerate(dataset.target_names):
X, y = dataset.data, dataset.target
clf.fit(X, y == idx)
rules = clf.rules_[0:3]
print("Rules for iris", species)
for rule in rules:
print( rule)print()
print(20*'=') print()
print()
 如果出現下列錯誤:
如果出現下列錯誤:
解決方案如下
import siximport sys
sys.modules['sklearn .externals.six'] = six
import mlrose親測有效!
如果使用「score_top_rules」方法,SkopeRules 也可以用作預測器:
from sklearn.datasets import load_boston
from sklearn.metrics import precision_recall_curve#plot#from pyplotplot plt
from skrules import SkopeRules
dataset = load_boston()
clf = SkopeRules(max_depth_duplicatinotallow=None,
n_estimators=30,
precision_min=0.2,##. n_estimators=30,
precision_min=0.2,#0. ,
feature_names=dataset.feature_names)
X, y = dataset.data, dataset.target > 25
X_train, y_train = X[:len(y)//2], y [:len(y)//2]
X_test, y_test = X[len(y)//2:], y[len(y)//2:]
clf.fit(X_train, y_train )
y_score = clf.score_top_rules(X_test) # Get a risk score for each test example
precision, recall, _ = precision_recall_curve(y_test, y_score)
plt.plot(recall, presionve()#cision plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision Recall curve')plt.show()
- 解決二分類問題
- 提取可解釋的決策規則
本案例分為5個部分
- 匯入相關庫
- 資料準備
- 模型訓練(使用ScopeRules().score_top_rules()方法)
- 解釋"生存規則"(使用SkopeRules().rules_屬性)。
- 效能分析(使用SkopeRules.predict_top_rules()方法)。
導入相關函式庫
# Import skope-rules
from skrules import SkopeRules
# Import librairies
import pandas as pd
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier##import matplotlib.pveplotplotplotps.
from matplotlib import cm
import numpy as np
from sklearn.metrics import confusion_matrix
from IPython.display import display
# Import Titanic data
data = pd.read_csv('
Import Titanic datadata = pd.read_csv('
資料準備
# 刪除年齡缺失的行
data = data.query('Age == Age')
# 為變數Sex建立編碼值
data['isFemale'] = (data['Sex'] == 'female') * 1
# 未變數Embarked建立編碼值
data = pd.concat(
[data,
pd.get_dummies(data.loc[:,'Embarked'],
dummy_na=False,
prefix='Embarked',
prefix_sep='_')],
axis=1
)
# 刪除沒有使用的變數
data = data.drop(['Name', 'Ticket', 'Cabin',
'PassengerId', 'Sex ', 'Embarked'],
axis = 1)
# 建立訓練及測試集
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['Survived'], axis =1),
data['Survived'],
test_size=0.25, random_state=42)
feature_names = X_train.columns
print('Column names are: ' ' '. join(feature_names.tolist()) '.')
print('Shape of training set is: ' str(X_train.shape) '.')
Column names are: Pclass Age SibSp Parch Fare
isFemale Embarked_C Embarked_Q Embarked_S.
Shape of training set is: (535, 9).
模型訓練
## 訓練一個梯度提升分類器,用於基準測試
gradient_boost_clf = GradientBoostingClassifier(random_state=42, n_estimators=30, max_depth = 5)
gradient_boost_clf.fit(X_train, y_train)
# 訓練一個隨機森林分類器,用於基準測試
random_forest_clf = RandomForestClassifier(random_state=42, n_estimators=30, max_depth = 5)
random_forest_clf.fit(X_train, y_train)
##cldetree DecisionTreeClassifier(random_state=42, max_depth = 5)
decision_tree_clf.fit(X_train, y_train)
## 訓練一個skope-rules-boosting 分類器
skope_rules_clf = Skopeles( 42, n_estimators=30,
recall_min=0.05, precision_min=0.9,
max_samples=0.7,
max_depth_duplicatinotallow= 4, max_depth = 5)#s#skope_rules_licatinotallow= 4, max_depth = 5)##skope_rules_licatinotallow
計算預測分數
gradient_boost_scoring = gradient_boost_clf.predict_proba(X_test)[:, 1]
random_forest_scoring = random_forest_clf.predict_proba(X_test)[Ftree:, 1]#.d wring =dm&Ft_prod)[ X_test)[:, 1]
skope_rules_scoring = skope_rules_clf.score_top_rules(X_test)
"生存規則" 的提取
## 獲得創建的生存規則的數量
print("用SkopeRules建立了" str(len(skope_rules_clf.rules_)) "條規則n")
# 列印這些規則
rules_explanations = [
"3歲以下和37歲以下,在頭等艙或二等艙的女性。 "
"3歲以上搭乘頭等艙或二等艙,支付超過26歐元的女性。 "
"坐一等艙或二等艙,支付超過29歐元的女性。 "
"年齡在39歲以上,在頭等艙或二等艙的女性。 "
]
print('其中表現最好的4條"泰坦尼克號生存規則" 如下所示:/n')
for i_rule, rule in enumerate(skope_rules_clf.rules_[:4] )
print(rule[0])
print('->' rules_explanations[i_rule] 'n')
用SkopeRules建立了9條規則。
其中表現最好的4條"泰坦尼克號生存規則" 如下所示:
Age 2.5
and Pclass 0.5
# -> 3歲以下和37歲以下,在頭等艙或二等艙的女性。
Age > 2.5 and Fare > 26.125
and Pclass 0.5
-> 3歲以上搭乘頭等艙或二等艙,支付超過26歐元的女性。
Fare > 29.356250762939453
and Pclass 0.5
-> 坐一等艙或二等艙,支付超過29歐元的女性。
Age > 38.5 and Pclass and isFemale > 0.5
-> 年齡在39歲以上,在頭等艙或二等艙的女性。
def compute_y_pred_from_query(X, rule):
score = np.zeros(X.shape[0])
X = X.reset_index(drop=True)
score[list( X.query(rule).index)] = 1
return(score)
def compute_performances_from_y_pred(y_true, y_pred, index_name='default_index'):
df = pd.DataFrame(data=
{
'precision':[sum(y_true * y_pred)/sum(y_pred)],
'recall':[sum(y_true * y_pred)/sum(y_true)]
},
index=[index_name],
columns=['precision', 'recall']
)
return(df)
def compute_train_test_query_performances(X_train, y_train, X_test, y_test , rule):
y_train_pred = compute_y_pred_from_query(X_train, rule)
y_test_pred = compute_y_pred_from_query(X_test, rule)
##performances = Nonedcatform. #performances,
compute_performances_from_y_pred(y_train, y_train_pred, 'train_set')],
axis=0)
performances = pd.concat([
performances,#test_)
performances = pd.concat([
performances,#test_test_compute_performance_pred_pred_pred_pred_m test_set')],
axis=0)
return(performances)
print('Precision = 0.96 表示規則決定的96%的人是倖存者。 ')
print('Recall = 0.12 表示規則識別的倖存者佔倖存者總數的12%n')
for i in range(4):
print('Rule ' str (i 1) ':')
display(compute_train_test_query_performances(X_train, y_train,
X_test, y_test,
skope_rules_clf.rules_[i][0])
)##skope_rules_clf.rules_[i][0])
)## = 0.96 表示規則確定的96%的人是倖存者。
Recall = 0.12 表示規則識別的倖存者佔倖存者總數的12%。
模型效能偵測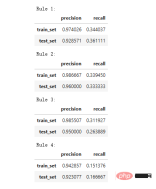
labels_with_line=['Gradient Boosting', 'Random Forest', 'Decision Tree'],
labels_with_points=['skope-rules']):gradient = np.linspace(0, 1, 10)
color_list = [ cm .tab10(x) for x in gradient ]
fig, axes = plt.subplots(1, 2, figsize=(12, 5),
sharex=True, sharey=True)
ax = axes[0]
n_line = 0
for i_score, score in enumerate(scores_with_line):
n_line = n_line 1
fpr, tpr, _ = roc_curve(y_true, score)
ax.plot(fpr, tpr, linestyle='-.', c=color_list[i_score], lw=1, label=labels_with_line[i_score])
for i_score, score in enumerate(scores_with_points):
fpr , tpr, _ = roc_curve(y_true, score)
ax.scatter(fpr[:-1], tpr[:-1], c=color_list[n_line i_score], s=10, label=labels_with_points[i_score] )
ax.set_title("ROC", fnotallow=20)
ax.set_xlabel('False Positive Rate', fnotallow=18)
ax.set_ylabel('True Positive Rate (Recall)', fnotallow =18)
ax.legend(loc='lower center', fnotallow=8)
ax = axes[1]
n_line = 0
for i_score, score in enumerate(scores_with_line ):
n_line = n_line 1
precision, recall, _ = precision_recall_curve(y_true, score)
ax.step(recall, precision, linestyle='-.', c=color_list[i_score], lw =1, where='post', label=labels_with_line[i_score])
for i_score, score in enumerate(scores_with_points):
precision, recall, _ = precision_recall_curve(y_true, score)##ax.scatter (recall, precision, c=color_list[n_line i_score], s=10, label=labels_with_points[i_score])
ax.set_title("Precision-Recall", fnotallow=20)
ax.set_xlabel('Recall (True Positive Rate)', fnotallow=18)
ax.set_ylabel('Precision', fnotallow=18)
ax.legend(loc='lower center', fnotallow=8)
plt.show ()
plot_titanic_scores(y_test,
scores_with_line=[gradient_boost_scoring, random_forest_scoring, decision_tree_scoring],
scores_with_points=[skope_rules_scoring]
#. ##在ROC曲線上,每個紅點對應於啟動的規則(來自skope-rules)的數量。例如,最低點是1個規則(最好的)的結果點。第二低點是2條規則結果點,以此類推。
在準確率-召回率曲線上,同樣的點是用不同的座標軸繪製的。警告:左邊的第一個紅點(0%召回率,100%精確度)對應0條規則。左邊的第二個點是第一個規則,等等。
從這個例子可以得到一些結論。
- skope-rules的表現比決策樹好。
- skope-rules的表現與隨機森林/梯度提升相似(在這個例子中)。
- 使用4個規則可以獲得很好的性能(61%的召回率,94%的精確度)(在這個例子中)。
n_rule_chosen = 4
y_pred = skope_rules_clf.predict_top_rules(X_test, n_rule_chosen)
print('The performances reached with ' strare_rulewing_rules 隨身 fver. ')
compute_performances_from_y_pred(y_test, y_pred, 'test_set')

predict_top_rules(new_data, n_r)方法用來計算對new_data的預測,其中n_r_rd skope-rules規則。
以上是漲知識!用邏輯規則進行機器學習的詳細內容。更多資訊請關注PHP中文網其他相關文章!
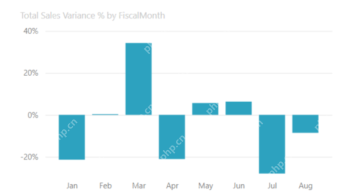 大多數使用的10個功率BI圖 - 分析VidhyaApr 16, 2025 pm 12:05 PM
大多數使用的10個功率BI圖 - 分析VidhyaApr 16, 2025 pm 12:05 PM用Microsoft Power BI圖來利用數據可視化的功能 在當今數據驅動的世界中,有效地將復雜信息傳達給非技術觀眾至關重要。 數據可視化橋接此差距,轉換原始數據i
 AI的專家系統Apr 16, 2025 pm 12:00 PM
AI的專家系統Apr 16, 2025 pm 12:00 PM專家系統:深入研究AI的決策能力 想像一下,從醫療診斷到財務計劃,都可以訪問任何事情的專家建議。 這就是人工智能專家系統的力量。 這些系統模仿Pro
 三個最好的氛圍編碼器分解了這項代碼中的AI革命Apr 16, 2025 am 11:58 AM
三個最好的氛圍編碼器分解了這項代碼中的AI革命Apr 16, 2025 am 11:58 AM首先,很明顯,這種情況正在迅速發生。各種公司都在談論AI目前撰寫的代碼的比例,並且這些代碼的比例正在迅速地增加。已經有很多工作流離失所
 跑道AI的Gen-4:AI蒙太奇如何超越荒謬Apr 16, 2025 am 11:45 AM
跑道AI的Gen-4:AI蒙太奇如何超越荒謬Apr 16, 2025 am 11:45 AM從數字營銷到社交媒體的所有創意領域,電影業都站在技術十字路口。隨著人工智能開始重塑視覺講故事的各個方面並改變娛樂的景觀
 如何註冊5天ISRO AI免費課程? - 分析VidhyaApr 16, 2025 am 11:43 AM
如何註冊5天ISRO AI免費課程? - 分析VidhyaApr 16, 2025 am 11:43 AMISRO的免費AI/ML在線課程:通向地理空間技術創新的門戶 印度太空研究組織(ISRO)通過其印度遙感研究所(IIR)為學生和專業人士提供了絕佳的機會
 AI中的本地搜索算法Apr 16, 2025 am 11:40 AM
AI中的本地搜索算法Apr 16, 2025 am 11:40 AM本地搜索算法:綜合指南 規劃大規模活動需要有效的工作量分佈。 當傳統方法失敗時,本地搜索算法提供了強大的解決方案。 本文探討了爬山和模擬
 OpenAI以GPT-4.1的重點轉移,將編碼和成本效率優先考慮Apr 16, 2025 am 11:37 AM
OpenAI以GPT-4.1的重點轉移,將編碼和成本效率優先考慮Apr 16, 2025 am 11:37 AM該版本包括三種不同的型號,GPT-4.1,GPT-4.1 MINI和GPT-4.1 NANO,標誌著向大語言模型景觀內的特定任務優化邁進。這些模型並未立即替換諸如
 提示:chatgpt生成假護照Apr 16, 2025 am 11:35 AM
提示:chatgpt生成假護照Apr 16, 2025 am 11:35 AMChip Giant Nvidia週一表示,它將開始製造AI超級計算機(可以處理大量數據並運行複雜算法的機器),完全是在美國首次在美國境內。這一消息是在特朗普總統SI之後發布的


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

Atom編輯器mac版下載
最受歡迎的的開源編輯器

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

Dreamweaver Mac版
視覺化網頁開發工具

記事本++7.3.1
好用且免費的程式碼編輯器






