一文搞懂Vue Diff演算法

這篇文章為大家帶來了關於vue的相關知識，其中主要介紹了關於diff演算法的相關問題，diff演算法的作用就是找出兩組vdom節點之間的差異，並且盡可能的複用dom節點，使得能用最小的效能消耗完成更新操作，下面一起來看一下，希望對大家有幫助。

【相關推薦：javascript影片教學、vue.js教學】

為什麼需要diff演算法？

對於一個容器（例如我們常用的#app）而言，它的內容一般有三種情況：

• 字串類型，即是文本。

• 子節點數組，即含有一個或多個子節點

• #null，即沒有子節點

在vue中，會將dom元素當作vdom來處理，我們的HTML Attributes、事件綁定都會現在vdom上進行操作處理，最後渲染成真實dom。

Virtual Dom：用來描述真實dom節點的JavaScript物件。

使用vdom的原因在於，如果每次操作都是直接對真實dom進行操作，那麼會造成很大的開銷。使用vdom時就能將效能消耗從真實dom操作的等級降低到JavaScript層面，相對而言更加優秀。一個簡單的vdom如下：

const vdom = {
    type:"div",
    props:{
        class: "class",
        onClick: () => { console.log("click") }
    },
    children: [] // 简单理解这就是上述三种内容
}

對於vue節點的更新而言，是採用的vdom進行比較。

diff演算法便是用於容器內容的第二種情況。當更新前的容器中的內容是一組子節點時，且更新後的內容仍是一組節點。如果不採用diff演算法，那麼最簡單的操作就是將先前的dom全部卸載，然後再將目前的新節點全部掛載。

但是直接操作dom物件是非常耗費效能的，所以diff演算法的作用就是找出兩組vdom節點之間的差異，並且盡可能的複用dom節點，使得能用最小的效能消耗完成更新操作。

接下來說三個diff演算法，從簡單到複雜循序漸進。

簡單的Diff演算法

為什麼需要key？

接下來透過兩種情況來說明為什麼需要key？

如果存在如下兩組新舊節點數組：

const oldChildren = [
    {type: 'p'},
    {type: 'span'},
    {type: 'div'},
]
const newChildren = [
    {type: 'div'},
    {type: 'p'},
    {type: 'span'},
    {type: 'footer'},
]

如果我們是進行正常的比較，步驟應該是這樣：

找到相對而言較短的一組進行循環比較

• 第一個p標籤與div標籤不符，需要先將p標籤卸載，再將div標籤掛載。

• 第一個spam標籤與p標籤不符，需要先將span標籤卸載，再掛載p標籤。

• 第一個div標籤與span標籤不符，需要先將div標籤卸載，然後將span標籤掛載。

• 最後多餘一個標籤footer存在在新節點陣列中，將其掛載即可。

那麼我們發現其中進行了7次dom操作，但是命名前三個都是可以重複使用的，只是位置改變了。如果進行複用節點我們需要判斷兩個節點是相等的，但是現在的已有條件還不能滿足。

所以我們需要引入key，它相當於是虛擬節點的身份證號，只要兩個虛擬節點的type和key都相同，我們便認為他們是相等的，可以進行dom的複用。

這時我們便可以找到復用的元素進行dom的移動，相對而言會比不斷的執行節點的掛載卸載要好。

但是，dom的複用不意味不需要更新：

const oldVNode = {type: 'p', children: 'old', key: 1}
const newVNode = {type: 'p', children: 'new', key: 2}

上述節點擁有相同的type和key，我們可以復用，此時進行子節點的更新即可。

簡單的diff演算法步驟

先用一個例子說明整個流程，再敘述其方法

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
    {type: 'section', children: 'section', key : 4},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'footer', children: 'footer', key: 5},
]

為了敘述簡單，這裡使用不同的標籤。整個流程如下：

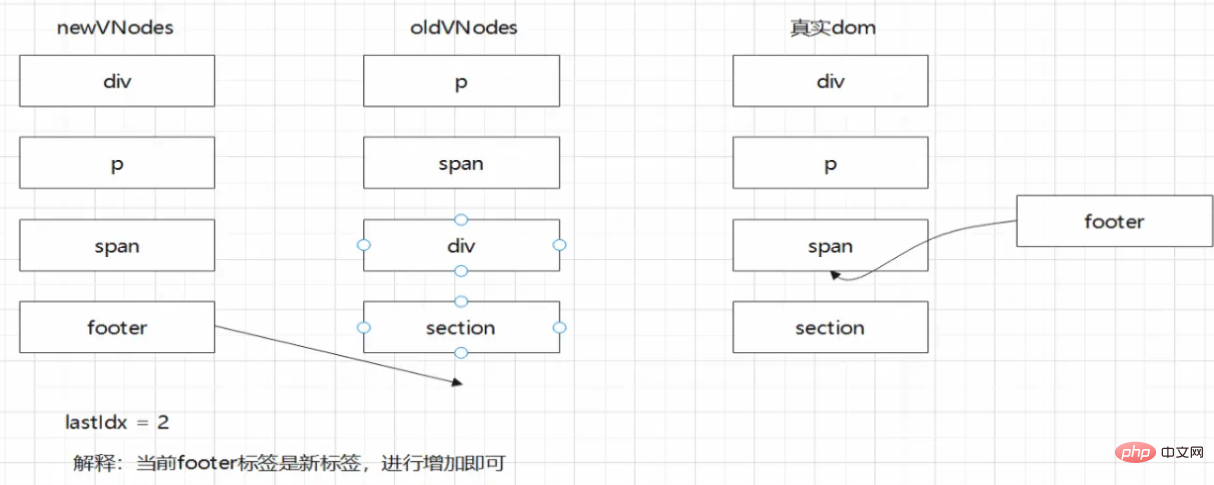
• 從新節點陣列開始遍歷

• 第一個是div標籤，目前的下標是0，之前的下標是2。相對位置並未改變，不需要移動，只需要就行更新節點內容。

• 第二個是p標籤，目前的下標是1，之前的下標是0。就相對位置而言，p相對於div標籤有變化，需要進行移動。移動的位置就是在div標籤之後。

• 第三个是span标签，当前的下标是2，之前的下标是1。就相对位置而言，p相对于div标签有变化，需要进行移动。移动的位置就是在p标签之后。

• 第四个标签是footer，遍历旧节点数组发现并无匹配的元素。代表当前的元素是新节点，将其插入，插入的位置是span标签之后。

• 最后一步，遍历旧节点数组，并去新节点数组中查找是否有对应的节点，没有则卸载当前的元素。

如何找到需要移动的元素？

上述声明了一个lastIdx变量，其初始值为0。作用是保存在新节点数组中，对于已经遍历了的新节点在旧节点数组的最大的下标。那么对于后续的新节点来说，只要它在旧节点数组中的下标的值小于当前的lastIdx，代表当前的节点相对位置发生了改变，则需要移动，

举个例子：div在旧节点数组中的位置为2，大于当前的lastIdx，更新其值为2。对于span标签，它的旧节点数组位置为1，其值更小。又因为当前在新节点数组中处于div标签之后，就是相对位置发生了变化，便需要移动。

当然，lastIdx需要动态维护。

总结

简单diff算法便是拿新节点数组中的节点去旧节点数组中查找，通过key来判断是否可以复用。并记录当前的lastIdx，以此来判断节点间的相对位置是否发生变化，如果变化，需要进行移动。

双端diff算法

简单diff算法并不是最优秀的，它是通过双重循环来遍历找到相同key的节点。举个例子：

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
]

其实不难发现，我们只需要将div标签节点移动即可，即进行一次移动。不需要重复移动前两个标签也就是p、span标签。而简单diff算法的比较策略即是从头至尾的循环比较策略，具有一定的缺陷。

顾名思义，双端diff算法是一种同时对新旧两组子节点的两个端点进行比较的算法

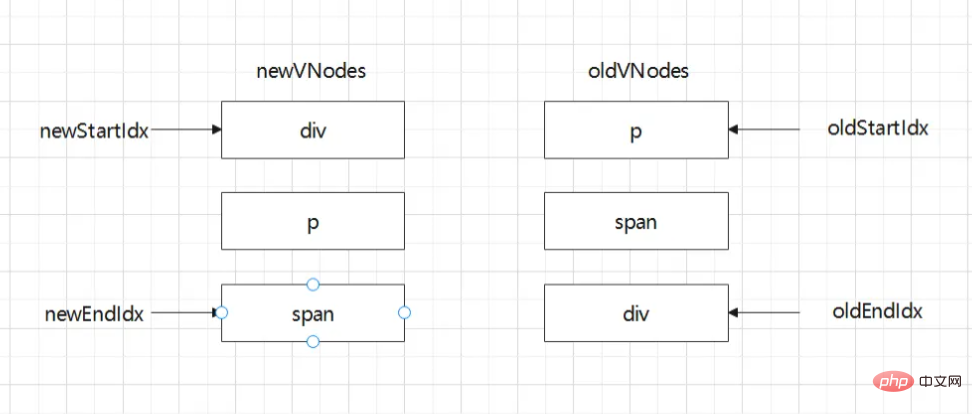
那么双端diff算法开始的步骤如下：

• 比较 oldStartIdx节点 与 newStartIdx 节点，相同则复用并更新，否则

• 比较 oldEndIdx节点 与 newEndIdx 节点，相同则复用并更新，否则

• 比较 oldStartIdx节点 与 newEndIdx 节点，相同则复用并更新，否则

• 比较 oldEndIdx节点 与 newStartIdx 节点，相同则复用并更新，否则

简单概括：

• 旧头 === 新头？复用，不需移动

• 旧尾 === 新尾？复用，不需移动

• 旧头 === 新尾？复用，需要移动

• 旧尾 === 新头？复用，需要移动

对于上述例子而言，比较步骤如下：

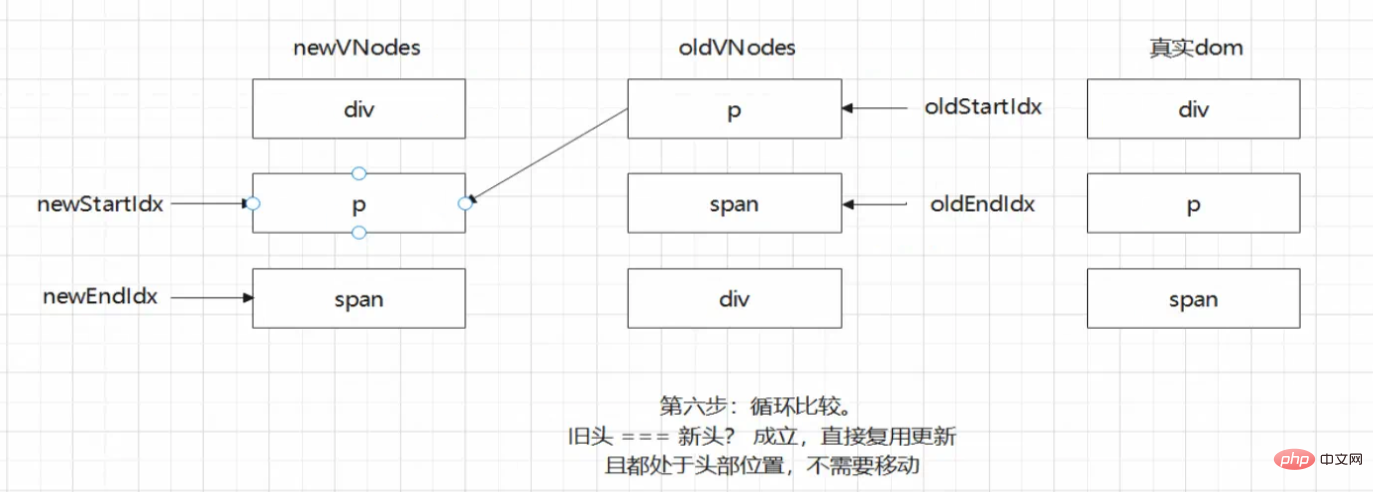
上述的情况是一种非常理想的情况，我们可以根据现有的diff算法完全的处理两组节点，因为每一轮的双端比较都会命中其中一种情况使得其可以完成处理。

但往往会有其他的情况，比如下面这个例子：

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
    {type: 'ul', children: 'ul', key: 4},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'ul', children: 'ul', key: 4},
    {type: 'span', children: 'span', key: 2},
]

此时我们会发现，上述的四个步骤都会无法命中任意一步。所以需要额外的步骤进行处理。即是：在四步比较失败后，找到新头节点在旧节点中的位置，并进行移动即可。动图示意如下：

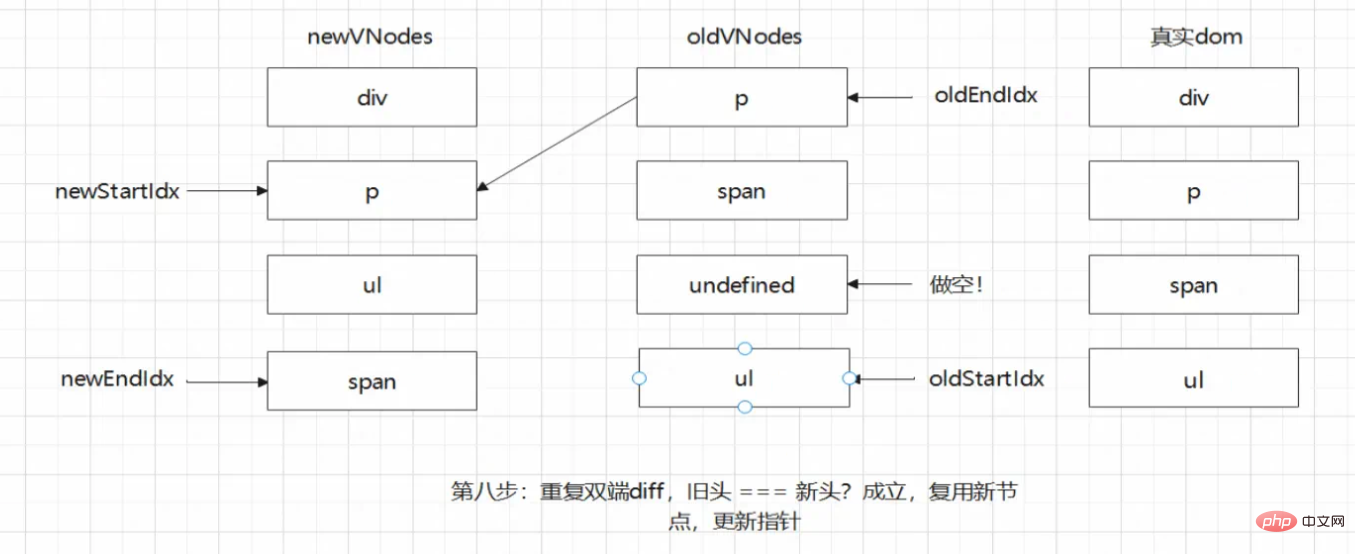
当然还有删除、增加等均不满足上述例子的操作，但操作核心一致，这里便不再赘述。

总结

双端diff算法的优势在于对于一些比较特殊的情况能更快的对节点进行处理，也更贴合实际开发。而双端的含义便在于通过两组子节点的头尾分别进行比较并更新。

快速diff算法

首先，快速diff算法包含了预处理步骤。它借鉴了纯文本diff的思路，这时它为何快的原因之一。

比如：

const text1 = '我是快速diff算法'
const text2 =  '我是双端diff算法'

那么就会先从头比较并去除可用元素，其次会重后比较相同元素并复用，那么结果就会如下：

const text1 = '快速'
const text2 = '双端'

此时再进行一些其他的比较和处理便会简单很多。

其次，快速diff算法还使用了一种算法来尽可能的复用dom节点，这个便是最长递增子序列算法。为什么要用呢？先举个例子：

// oldVNodes
const vnodes1 = [
    {type:'p', children: 'p1', key: 1},
    {type:'div', children: 'div', key: 2},
    {type:'span', children: 'span', key: 3},
    {type:'input', children: 'input', key: 4},
    {type:'a', children: 'a', key: 6}
    {type:'p', children: 'p2', key: 5},
]
// newVNodes 
const vnodes2 = [
    {type:'p', children: 'p1', key: 1},
    {type:'span', children: 'span', key: 3},
    {type:'div', children: 'div', key: 2},
    {type:'input', children: 'input', key: 4},
    {type:'p', children: 'p2', key: 5},
]

经过预处理步骤之后得到的节点如下：

// oldVNodes
const vnodes1 = [
    {type:'div', children: 'div', key: 2},
    {type:'span', children: 'span', key: 3},
    {type:'input', children: 'input', key: 4},
    {type:'a', children: 'a', key: 6},
]
// newVNodes 
const vnodes2 = [
    {type:'span', children: 'span', key: 3},
    {type:'div', children: 'div', key: 2},
    {type:'input', children: 'input', key: 4},
]

此时我们需要获得newVNodes节点相对应oldVNodes节点中的下标位置，我们可以采用一个source数组，先循环遍历一次newVNodes，得到他们的key，再循环遍历一次oldVNodes，获取对应的下标关系，如下：

const source = new Array(restArr.length).fill(-1)
// 处理后
source = [1, 2, 0, -1]

注意！这里的下标并不是完全正确！因为这是预处理后的下标，并不是刚开始的对应的下标值。此处仅是方便讲解。 其次，source数组的长度是剩余的newVNodes的长度，若在处理完之后它的值仍然是-1则说明当前的key对应的节点在旧节点数组中没有，即是新增的节点。

此时我们便可以通过source求得最长的递增子序列的值为 [1, 2] 。对于index为1，2的两个节点来说，他们的相对位置在原oldVNodes中是没有变化的，那么便不需要移动他们，只需要移动其余的元素。这样便能达到最大复用dom的效果。

步骤

以上述例子来说：

• 首先进行预处理

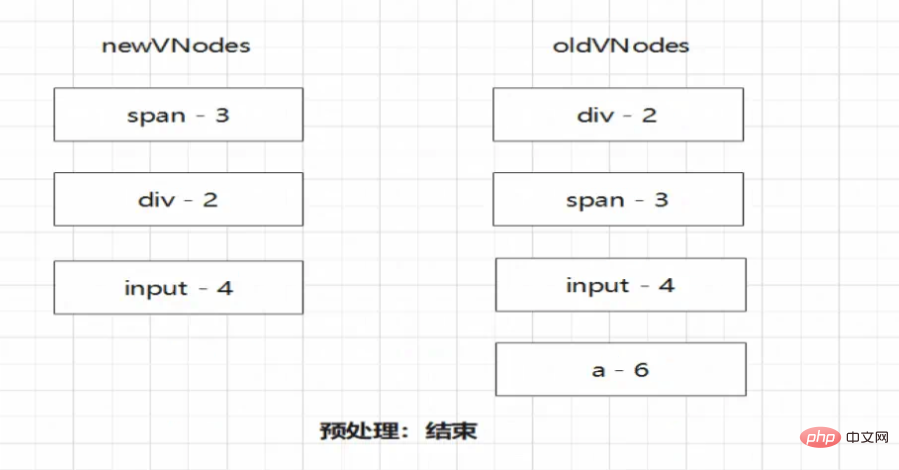
注意！预处理过的节点虽然复用，但仍然需要进行更新。

• 进行source填充

当然这里递增子序列 [1, 2] 和 [0, 1]都是可以的。

• 进行节点移动

用索引i指向新节点数组中的最后一个元素

用索引s指向最长递增子序列中的最后一个元素

然后循环进行以下步骤比较：

source[i] === -1？等于代表新节点，挂载即可。随后移动i

i === 递增数组[s]? 等于代表当前的节点存在在递增子序列中，是复用的节点，当前的节点无需移动。

上述均不成立代表需要移动节点。

节点更新，结束。

总结

核心思路便是进行了类似文本预处理的步骤去除头尾重复的节点。其次便是采用了最长递增子序列来复用相对位置没有发生变化的节点，这些节点是不需要移动的，便能最快的复用和更新。

最后

其实不论是哪一种diff算法，它都需要遵循同样的处理规则：

判断哪些节点需要移动，以及如何移动。

找出那些需要被添加的或者被移除的节点。

【相关推荐：javascript视频教程、vue.js教程】

以上是一文搞懂Vue Diff演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！