python檢定Jarque-Bera是否符合常態分佈
- 零到壹度原創
- 2018-04-09 16:19:0612066瀏覽
本篇文章給大家分享的內容是python檢驗Jarque-Bera是否符合常態分佈,有著一定的參考價值,有需要的朋友可以參考一下
#常態分佈是一種總體分佈的常態性檢定。當序列服從常態分佈時,JB統計量:
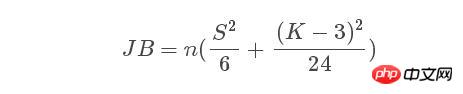
漸進服從分佈。其中n為樣本規模,S,K分別為隨機變數的偏度和峰度。計算公式如下:
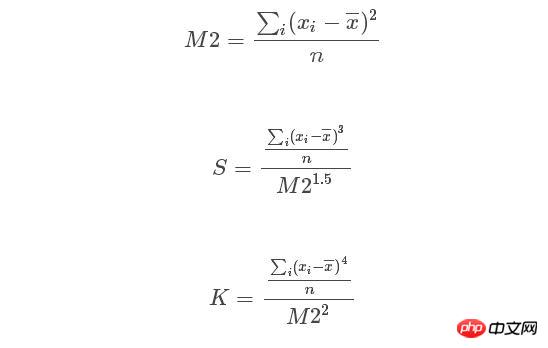
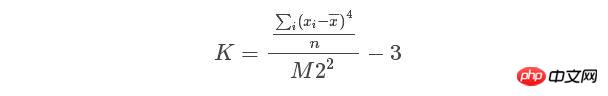
python的sicipy.stats中偏度和峰度的調用的函數為stats.skew(y)
、stats.kurtosis(y)############# ##下面自己實作一遍python的scipy函式庫中計算偏度和斜的公式及建立常態分佈檢定。 ######程式碼###,其中峰度的公式為
#在excel中,偏態和峰度的計算公式如下:
import numpy as npimport scipy.stats as statsdef self_JBtest(y):
# 样本规模n
n = y.size
y_ = y - y.mean() """
M2:二阶中心钜
skew 偏度 = 三阶中心矩 与 M2^1.5的比
krut 峰值 = 四阶中心钜 与 M2^2 的比
"""
M2 = np.mean(y_**2)
skew = np.mean(y_**3)/M2**1.5
krut = np.mean(y_**4)/M2**2
"""
计算JB统计量,以及建立假设检验
"""
JB = n*(skew**2/6 + (krut-3 )**2/24)
pvalue = 1 - stats.chi2.cdf(JB,df=2)
print("偏度:",stats.skew(y),skew)
print("峰值:",stats.kurtosis(y)+3,krut)
print("JB检验:",stats.jarque_bera(y)) return np.array([JB,pvalue])
y1 = stats.norm.rvs(size=10)
y2 = stats.t.rvs(size=1000,df=4)
print(self_JBtest(y1))
print(self_JBtest(y2))###結果######=============== RESTART: C:\Users\tinysoft\Desktop\JB正态性检验.py =============== 偏度: 0.5383125387398069 0.53831253874 峰值: 2.9948926317585918 2.99489263176 JB检验: (0.48297818444514068, 0.78545737133644544) [ 0.48297818 0.78545737] 偏度: -1.0488825341925703 -1.04888253419 峰值: 13.40804986639119 13.4080498664 JB检验: (4697.0050126426095, 0.0) [ 4697.00501264 0. ]###
以上是python檢定Jarque-Bera是否符合常態分佈的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文內容由網友自願投稿,版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容,請聯絡admin@php.cn