數十年來首次取得進展，陶哲軒高徒、趙宇飛高徒突破組合數學難題

近期，一個數十年來未解決的數學難題首次取得了進展。

推動這項進展的是來自加州大學洛杉磯分校的研究生 James Leng 和麻省理工學院數學研究生 Ashwin Sah、哥倫比亞大學助理教授 Mehtaab Sawhney。其中James Leng 師從著名數學家陶哲軒，Ashwin Sah 師從離散數學大牛趙宇飛。

論文地址：https://arxiv.org/pdf/2402.17995

要了解這項研究取得的突破，需要從算術級數說起。

等差數列的前 n 項和稱為一個等差級數，也稱為算術級數。 1936 年，數學家 Paul Erdős 和 Pál Turán 猜想：如果一個集合由整數的非零分數組成（即使是 0.00000001%），那麼它一定包含任意長的算術級數。唯一可以避免算術級數的集合是那些包含整數「可忽略不計」部分的集合。例如，集合 {2, 4, 8, 16, …}，其中每個數字都是前一個數字的兩倍，它沿著數軸分散，沒有級數。

1975 年，數學家 Endre Szemerédi 證明了這個猜想。他的工作催生了數學家至今仍在探索的多種研究方向。

數學家們在有限數集（從 1 到某個數 N 之間的所有整數）的情況下建立了 Szemerédi 的結果。在不可避免地包含一個被禁止的級數之前，集合中可以使用的部分佔初始池的多少？隨著 N 的變化，這個佔比會如何改變？

例如，令 N 為 20，那麼可以寫下這 20 個數字中的多少個，同時仍然避免長度為 5 個或更多數字的級數？事實證明，答案是初始池的 16% 到 80%。

Szemerédi 是第一個證明隨著 N 的增長，這個佔比必須縮小到零的人，後來數學家們一直試圖量化該情況發生的速度。

去年，兩位電腦科學家的突破性工作幾乎解決了三個等級的問題，例如 {6, 11, 16}。但當你試圖避免四項或更多項的算術級數時，問題就變得更加困難。這是因為較長的級數反映了經典數學方法難以揭示的潛在結構。

三項算術級數中的數字x、y 和z 總是滿足簡單方程式x – 2y + z = 0（以級數{10, 20, 30} 為例：10 – 2*(20 ) + 30 = 0），證明一個集合是否包含滿足這種條件的數字相對容易。而四項級數中的數字也必須滿足更複雜的方程式 x^2 – 3y^2 + 3z^2 – w^2 = 0，具有五項或更多項的級數必須滿足更複雜的方程式。這意味著包含此類級數的集合會表現出更微妙的模式。數學家也更難證明這種模式是否存在。

20 世紀 90 年代末，數學家 Timothy Gowers 提出了一種克服這一障礙的理論。後來他被授予菲爾茲獎，這是數學界的最高榮譽，部分原因是因為這項工作。 2001 年，他將自己的方法應用於 Szemerédi 定理，證明了最大集合大小的更好界限，避免了任何給定長度的算術級數。

2022 年，當時正讀加州大學洛杉磯分校研究生二年級的 James Leng 開始理解 Gowers 的理論。他沒有考慮 Szemerédi 定理。相反，他希望回答與 Gowers 的方法相關的問題。

然而，努力探索了一年多，他一無所獲。

一直在思考相關問題的 Sah 和 Sawhney 了解了 Leng 的工作，他們很感興趣，Sawhney 甚至說：「我很驚訝竟然可以這樣思考」。

Sah 和 Sawhney 意識到 Leng 的研究可能有助於他們在 Szemerédi 定理上取得進一步進展。幾個月之內，三位年輕的數學家就想出瞭如何在沒有五項級數的情況下獲得更好的集合大小上限。然後，他們將工作擴展到任意長度的級數，這標誌著自 Gowers 證明以來 23 年來該問題的首次取得進展。

設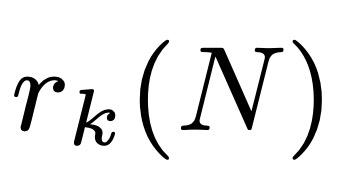表示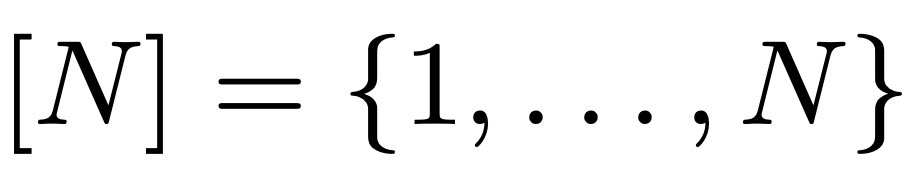，沒有 k 項算術級數的最大子集的大小。 Leng、Sah 和 Sawhney 證明，對於 k ≥ 5，存在 c_k > 0 使得。

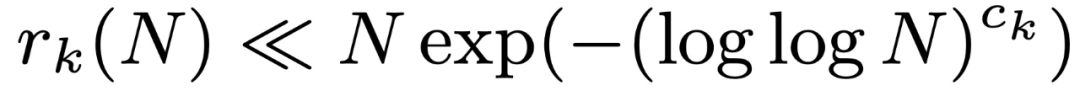研究團隊

論文一作 James Leng 是加州大學洛杉磯分校 (UCLA) 的數學研究生，本科畢業於加州大學柏克萊分校。他師從著名數學家陶哲軒。

James Leng 的研究興趣包括算術組合學、動力系統和傅立葉分析等等。他的研究也曾得到 NSF 研究生獎學金的支持。

                      ^🎜>

Ashwin Sah 從小就喜歡數學，他在競賽中接觸了高等數學並表現優異。 2016 年夏天，16 歲的 Sah 贏得國際奧林匹克數學競賽（IMO）的金牌，隔年他進入 MIT 求學。

                      Sah 的數學發展起到重要作用。第一個是離散數學大牛趙宇飛（Yufei Zhao）教授，他也是 Sah 的研究生導師。 第二個是 Mehtaab Sawhney，他們在課堂上相遇並成為朋友。後來，兩人一起做研究，共同探討離散數學領域內的多個主題，如圖論、機率論和隨機矩陣的屬性。 2017 年底，Ashwin Sah 和 Mehtaab Sawhney 在（MIT）讀本科時相識。從那時起，兩人一起編寫了令人難以置信的 57 個數學證明，其中許多在各個領域產生了深遠的影響。

                        Mehtaab Sawhney

Mehtaab Sawhney 現在是哥倫比亞大學助理教授。他的研究興趣包括組合學、機率和理論計算機科學等等。

參考連結：https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/

以上是數十年來首次取得進展，陶哲軒高徒、趙宇飛高徒突破組合數學難題的詳細內容。更多資訊請關注PHP中文網其他相關文章！