以 3 個 Excel 財務函數解決複雜財務計算

原文標題：《這 3 個 Excel 財務函數，又是被低估了的函數！ 》

本文作者：小花

本文編輯：竺蘭

最近小花遇到一個有趣的問題，是來自一位老朋友的靈魂發問：

怎麼在月交年金和民間互保金融中做出選擇？

這兩個理財產品的基本情況如下：

月交年金：

每月繳納 1000 元，年化利率 3%，2 年期，到期一次性提取本息。

互保金融：

每月繳納本金 1000 元，每月本金均以 10% 計息，2 年期。同一產品共有 24 人參與，每個月必須有 1 人領取其他人繳納的全部本息，領取之後的次月，必須支付 100 元 / 月的利息。

如何比較這兩種理財產品的優劣呢？

我們可以從終值法、收益率法和 IRR 法來考慮這個問題，順便給大家分享一些財務函數用法。

1、終值法

終值分析法是在確定了基準年、折算利率、現金流程以後，計算方案（項目）的淨效益終值。終值越高，方案的經濟可行性越大。

等額年金到期後能夠收到多少本息呢？這問題，可以用終值函數 FV 來計算。

年金終值公式：

=-FV(B3/12,C3,A3)

2 年後，總共可以收到本息24,703 元。

「互保金融」的終值（假設不滾動投資）與領取本息的先後有關係，越晚提取，收益越大。其終值計算如下：

=S2*U2+S2*T2*(V2-1)-S2*T2*(U2-V2)

從終值法來看，如果能確保領取期在16 期以後，「互保金融」的收益大於月交年金，當領取期早於16 期，「互保金融」的收益小於月交年金。

終值法適用投資規模相當的投資方案。

2、收益率法

當我把這個初步的結論告訴我這位老朋友時，他難以置信地問到：

為什麼「互保金融」的名目利率有10%，卻只有1/3 的參與者收益高於月繳年金，後者的收益率只有3%？

這就牽涉到收益率的計算。

收益率法就是將投資項目的年平均淨收益率與該投資的資金成本加以比較，判斷投資是否可取，然後在可取投資方案中選擇收益率大的投資方案的一種投資決策方法。

顯而易見，月交年金的殖利率與名目利率一致，為 3%。

那麼，「互保金融」的各領取期報酬率是多少呢？

我們可以用

RATE 函數來計算。

「互保金融」的殖利率計算如下：

=RATE(U2-S2,0,W2,0)*12

「互保金融」的名目利率高達10%，但實際上，只有當參與人在16 期以後領取本息，收益率才能達到3%，在此之前領取的，收益率均低於月交年金的收益率3%。可見，「互保金融」收益率還是有水分的。 但就此評價「互保金融」收益不如月繳年金，有失公允，原因在於，月交年金要到期後才能收回本息，而「互保金融」則可能提前實現資金流入，如果這部分資金再次用於投資，「互保金融」將大有改善。

財務管理上，常用時間價值來解釋這種差異，可使用內部報酬率 IRR 和淨現值 NPV 來衡量某項投資的動態收益。

以下，我們選用

NPV

來比較這兩個理財產品，IRR 比較法不適用本案例。

3、淨現值法

計算淨現值前，我們需要列出兩個產品各期的現金流，再使用 NPV 函數來計算。

The monthly payment for monthly annuity is 1,000 yuan. After 24 payments, the principal and interest of 24,703 yuan will be recovered in one lump sum. The cash flow and NPV are calculated as follows:

=NPV(B3/12,B2:Y2)

Here, the interest rate of monthly annuity is directly selected as the discount rate, and its net present value should be 0. When calculating the net present value of "Mutual Insurance Finance", we continue to use this discount rate. If the latter's net present value is greater than 0, it means that the investment income of the latter is better, otherwise it is worse.

"Mutual Insurance Finance" has multiple possible withdrawal periods, so when calculating the IRR of this product, we need to use a simulation table to achieve it.

"Mutual Insurance Finance" NPV calculation:

❶ Taking the withdrawal period as the variable, the cash flow of each period calculated based on the variable is listed.

The cash flow of the principal, a positive number indicates payment, and a negative number indicates withdrawal.

=IF(E$4=$G$2,-$D$2*23,$D$2)

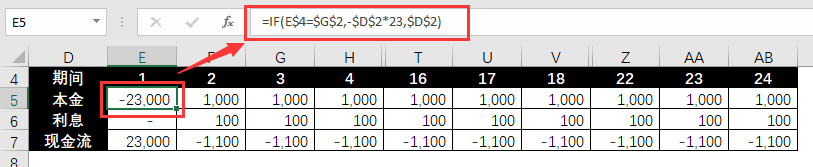
The cash flow of interest, a positive number indicates payment, and a negative number indicates receipt.

=IFS(E4$G$2,$D$2*$E$2)

Consolidated cash flow:

❷ Calculate the IRR under a single withdrawal period.

=NPV(H2/12,E7:AB7)

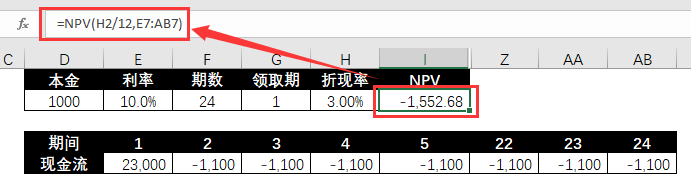
❸ Use the simulation table to calculate the NPV corresponding to different extraction periods.

① List the required collection period variable values ​​and link the corresponding result values ​​in the first row.

② Select the link row, variable value area and result value area, and follow the steps below to complete the simulation operation.

The simulation calculation results are as follows:

From an NPV perspective, the income of "mutual insurance finance" and monthly annuity are comparable.

Among all the participants in the former, their comparative returns are mixed. This is because participants with earlier receiving periods can obtain cash inflows faster for rolling investment, which to a certain extent hedges against the loss of high interest rates. .

To sum up, when it is impossible to realize rolling investment or pursue certainty, you should choose monthly annuity for investment. This product has stable investment income and higher average static income.

If you pursue higher dynamic returns or are able to make secondary investments after withdrawing principal and interest, you should choose "Mutual Insurance Finance" for financial management. The latter has the opportunity to achieve higher net present value and static returns.

The above is an extension of Xiaohua from a financial product selection problem. It explains the usage of several Excel financial formulas and functions, including:

❶ FV function and RATE function

❷ NPV function

❸ Simulation table

If you are a financial accountant, or have a need or interest in financial calculations, these formulas and practical cases will be helpful to you.

Xiaohua will continue to share other practical cases of Excel financial income calculation, and use practical experience to help you get through the use of formulas and tools, so stay tuned!

以上是以 3 個 Excel 財務函數解決複雜財務計算的詳細內容。更多資訊請關注PHP中文網其他相關文章！