Model resapan membuka era baharu model generatif dengan prestasi cemerlangnya dalam penjanaan imej. Model besar seperti Stable Diffusion, DALLE, Imagen, SORA, dll. telah muncul, memperkayakan lagi prospek aplikasi AI generatif. Walau bagaimanapun, model resapan semasa tidak sempurna secara teori, dan beberapa kajian telah memberi perhatian kepada masalah singulariti tidak ditentukan pada titik akhir masa pensampelan. Di samping itu, purata tahap kelabu yang disebabkan oleh masalah singulariti dalam aplikasi dan masalah lain yang menjejaskan kualiti imej yang dijana belum dapat diselesaikan. Untuk menyelesaikan masalah ini, pasukan WeChat Vision bekerjasama dengan Universiti Sun Yat-sen untuk bersama-sama meneroka masalah singulariti dalam model resapan dan mencadangkan kaedah plug-and-play yang berkesan menyelesaikan masalah pensampelan di detik awal. Kaedah ini berjaya menyelesaikan masalah tahap kelabu purata dan meningkatkan keupayaan penjanaan model resapan sedia ada dengan ketara. Hasil penyelidikan telah dibentangkan pada persidangan CVPR 2024. Model penyebaran telah mencapai kejayaan ketara dalam tugas penjanaan kandungan berbilang modal, termasuk penjanaan imej, audio, teks dan video. Kejayaan pemodelan model ini kebanyakannya bergantung pada andaian bahawa proses songsang proses resapan juga mematuhi sifat Gaussian. Namun, hipotesis ini belum dapat dibuktikan sepenuhnya. Terutamanya pada titik akhir, iaitu, t=0 atau t=1, masalah singulariti akan berlaku, yang mengehadkan kaedah sedia ada untuk mengkaji persampelan pada singulariti. Selain itu, masalah singulariti juga akan menjejaskan keupayaan penjanaan model resapan, menyebabkan model tersebut mengalami masalah skala kelabu purata, iaitu sukar untuk menghasilkan imej dengan kecerahan yang kuat atau lemah, kerana ditunjukkan dalam rajah di bawah. Ini juga mengehadkan skop aplikasi model penyebaran semasa ke tahap tertentu. Untuk menyelesaikan masalah singulariti model penyebaran pada titik akhir masa, pasukan visi WeChat bekerjasama dengan Universiti Sun Yat-sen dan menjalankan penyelidikan mendalam dari kedua-dua aspek teori dan praktikal. Pertama, pasukan mencadangkan batas atas ralat yang merangkumi anggaran taburan Gaussian bagi proses songsang pada momen singulariti, yang menyediakan asas teori untuk penyelidikan seterusnya. Berdasarkan jaminan teori ini, pasukan mengkaji pensampelan pada titik tunggal dan mencapai dua kesimpulan penting: 1) Titik tunggal pada t=1 boleh diubah menjadi titik tunggal boleh tanggal dengan mencari had, 2) Ketunggalan pada t=0 adalah sifat yang wujud dalam model resapan dan tidak perlu dielakkan. Berdasarkan kesimpulan ini, pasukan mencadangkan kaedah plug-and-play: SingDiffusion, untuk menyelesaikan masalah pensampelan model resapan pada saat awal. Sebilangan besar pengesahan percubaan telah menunjukkan bahawa modul SingDiffusion boleh digunakan dengan lancar pada model resapan sedia ada dengan hanya satu latihan, menyelesaikan masalah purata nilai kelabu dengan ketara. Tanpa menggunakan teknologi bimbingan tanpa pengelas, SingDiffusion dapat meningkatkan kualiti penjanaan kaedah semasa dengan ketara Terutamanya selepas digunakan pada Stable Diffusion1.5 (SD-1.5), kualiti imej yang dihasilkan dipertingkatkan sebanyak 33%. Alamat kertas: https://arxiv.org/pdf/2403.08381.pdf
 Alamat projek: https://pangzecheung.github.io/SingDiffusion/Tajuk kertas: Menangani Singulariti pada Titik Akhir Selang Masa dalam Diffusion ModelSifat Gaussian bagi proses songsang
Alamat projek: https://pangzecheung.github.io/SingDiffusion/Tajuk kertas: Menangani Singulariti pada Titik Akhir Selang Masa dalam Diffusion ModelSifat Gaussian bagi proses songsang
Untuk mengkaji masalah singulariti model resapan, adalah perlu untuk mengesahkan bahawa proses songsang keseluruhan proses termasuk ketunggalan memuaskan. harta benda. Pertama, takrifkan
sebagai sampel latihan model resapan Taburan sampel latihan boleh dinyatakan sebagai:
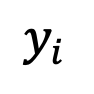 .Di mana δ mewakili fungsi Dirac. Mengikut takrifan model resapan masa berterusan dalam [1], untuk mana-mana dua saat 0≤s,t≤1, proses ke hadapan boleh dinyatakan sebagai: di mana
.Di mana δ mewakili fungsi Dirac. Mengikut takrifan model resapan masa berterusan dalam [1], untuk mana-mana dua saat 0≤s,t≤1, proses ke hadapan boleh dinyatakan sebagai: di mana 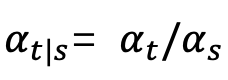 ,
, 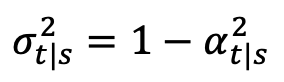 ,
, 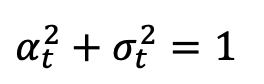 ,
, 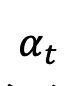 adalah monotonik dengan masa Tukar dari 1 kepada 0. Memandangkan taburan sampel latihan yang baru ditakrifkan, ketumpatan kebarangkalian marginal momen tunggal bagi
adalah monotonik dengan masa Tukar dari 1 kepada 0. Memandangkan taburan sampel latihan yang baru ditakrifkan, ketumpatan kebarangkalian marginal momen tunggal bagi 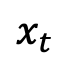 boleh dinyatakan sebagai:
boleh dinyatakan sebagai: 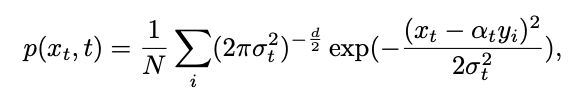
Daripada ini, taburan bersyarat bagi proses songsang boleh dikira melalui formula Bayes:
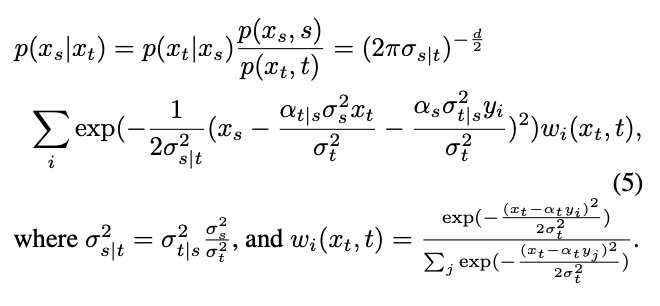
Walau bagaimanapun, selepas Pengagihan adalah campuran pengagihan Gaussian, yang sukar untuk dimuatkan dengan rangkaian. Oleh itu, model resapan arus perdana biasanya mengandaikan bahawa taburan ini boleh dimuatkan oleh satu taburan Gaussian.
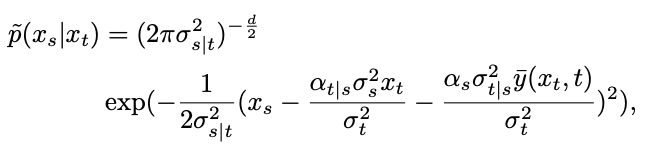
di mana, 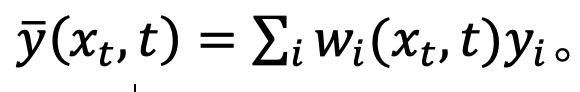 Untuk menguji hipotesis ini, kajian menganggarkan ralat kesesuaian ini dalam Proposisi 1.
Untuk menguji hipotesis ini, kajian menganggarkan ralat kesesuaian ini dalam Proposisi 1. 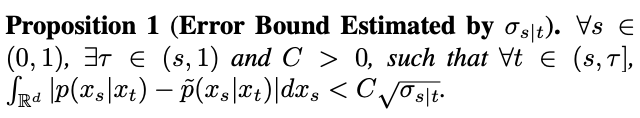
Namun, kajian mendapati apabila t=1, apabila s menghampiri 1, 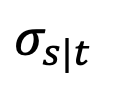 juga akan menghampiri 1, dan ralat itu tidak boleh diabaikan. Oleh itu, Proposisi 1 tidak membuktikan sifat Gaussian songsang pada t=1. Untuk menyelesaikan masalah ini, kajian ini memberikan cadangan baru:
juga akan menghampiri 1, dan ralat itu tidak boleh diabaikan. Oleh itu, Proposisi 1 tidak membuktikan sifat Gaussian songsang pada t=1. Untuk menyelesaikan masalah ini, kajian ini memberikan cadangan baru: 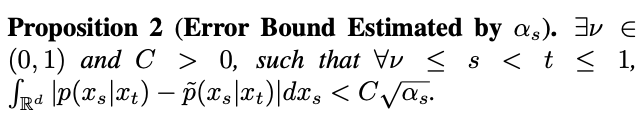
Menurut Proposisi 2, apabila t=1, apabila s menghampiri 1, 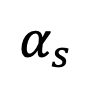 akan menghampiri 0. Oleh itu, kajian ini membuktikan bahawa keseluruhan proses songsang termasuk momen singulariti menepati ciri Gaussian. Pensampelan pada Momen Singulariti Dengan jaminan ciri Gaussian bagi proses songsang, kajian ini menjalankan kajian terhadap persampelan pada momen singulariti berdasarkan formula persampelan songsang. Pertimbangkan dahulu masalah singulariti pada masa t=1. Apabila t=1,
akan menghampiri 0. Oleh itu, kajian ini membuktikan bahawa keseluruhan proses songsang termasuk momen singulariti menepati ciri Gaussian. Pensampelan pada Momen Singulariti Dengan jaminan ciri Gaussian bagi proses songsang, kajian ini menjalankan kajian terhadap persampelan pada momen singulariti berdasarkan formula persampelan songsang. Pertimbangkan dahulu masalah singulariti pada masa t=1. Apabila t=1,  =0, formula pensampelan berikut akan mempunyai penyebut dibahagikan dengan 0:
=0, formula pensampelan berikut akan mempunyai penyebut dibahagikan dengan 0: 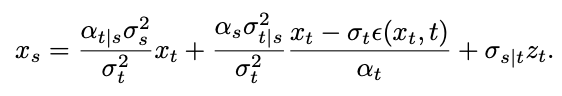
Pasukan penyelidik mendapati bahawa dengan mengira had, titik tunggal boleh diubah menjadi titik tunggal boleh tanggal: 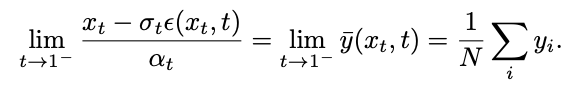
Walau bagaimanapun, had ini tidak boleh dikira semasa ujian. Untuk tujuan ini, kajian ini mencadangkan bahawa kita boleh muat 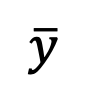 pada masa t=1 dan menggunakan "ramalan-x" untuk menyelesaikan masalah pensampelan pada titik tunggal awal. Kemudian pertimbangkan masa t=0, proses songsang pemasangan taburan Gaussian akan menjadi taburan Gaussian dengan varians 0, iaitu fungsi Dirac:
pada masa t=1 dan menggunakan "ramalan-x" untuk menyelesaikan masalah pensampelan pada titik tunggal awal. Kemudian pertimbangkan masa t=0, proses songsang pemasangan taburan Gaussian akan menjadi taburan Gaussian dengan varians 0, iaitu fungsi Dirac: 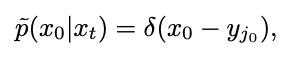
di mana 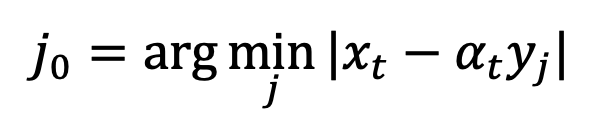 . Singulariti sedemikian akan menyebabkan proses pensampelan menumpu kepada data yang betul
. Singulariti sedemikian akan menyebabkan proses pensampelan menumpu kepada data yang betul 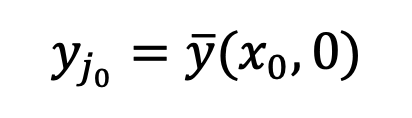 . Oleh itu, ketunggalan pada t=0 adalah sifat yang baik bagi model resapan dan tidak perlu dielakkan. Selain itu, kajian juga meneroka masalah singulariti dalam DDIM, SDE, ODE dalam lampiran. Plug-and-play SingDiffusion modulePensampelan pada titik tunggal akan menjejaskan kualiti imej yang dijana oleh model resapan. Contohnya, apabila memasukkan isyarat kecerahan tinggi atau rendah, kaedah sedia ada selalunya hanya boleh menjana imej dengan skala kelabu purata, yang dipanggil masalah skala kelabu purata. Masalah ini berpunca daripada fakta bahawa kaedah sedia ada mengabaikan pensampelan pada titik tunggal pada t=0, dan sebaliknya menggunakan taburan Gaussian standard sebagai taburan awal untuk pensampelan pada masa 1-ϵ. Walau bagaimanapun, seperti yang ditunjukkan dalam rajah di atas, terdapat jurang yang besar antara taburan Gaussian standard dan taburan data sebenar pada masa 1-ϵ.
. Oleh itu, ketunggalan pada t=0 adalah sifat yang baik bagi model resapan dan tidak perlu dielakkan. Selain itu, kajian juga meneroka masalah singulariti dalam DDIM, SDE, ODE dalam lampiran. Plug-and-play SingDiffusion modulePensampelan pada titik tunggal akan menjejaskan kualiti imej yang dijana oleh model resapan. Contohnya, apabila memasukkan isyarat kecerahan tinggi atau rendah, kaedah sedia ada selalunya hanya boleh menjana imej dengan skala kelabu purata, yang dipanggil masalah skala kelabu purata. Masalah ini berpunca daripada fakta bahawa kaedah sedia ada mengabaikan pensampelan pada titik tunggal pada t=0, dan sebaliknya menggunakan taburan Gaussian standard sebagai taburan awal untuk pensampelan pada masa 1-ϵ. Walau bagaimanapun, seperti yang ditunjukkan dalam rajah di atas, terdapat jurang yang besar antara taburan Gaussian standard dan taburan data sebenar pada masa 1-ϵ. 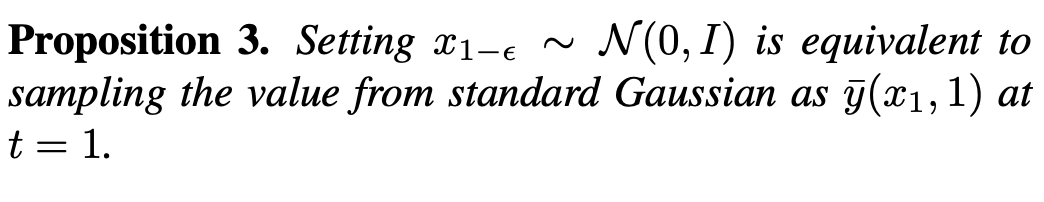
Di bawah jurang sedemikian, menurut Proposisi 3, kaedah sedia ada adalah bersamaan dengan menjana imej dengan nilai min 0 pada t=1, iaitu imej skala kelabu purata. Oleh itu, kaedah sedia ada sukar untuk menghasilkan imej dengan kecerahan yang sangat kuat atau lemah. Untuk menyelesaikan masalah ini, kajian ini mencadangkan kaedah SingDiffusion plug-and-play untuk merapatkan jurang ini dengan menyesuaikan penukaran antara taburan Gaussian standard dan taburan data sebenar. Algoritma SingDiffuion ditunjukkan dalam rajah di bawah:

Mengikut kesimpulan bahagian sebelum ini, kajian ini menggunakan kaedah "x - prediction" pada t=1 untuk menyelesaikan masalah persampelan di titik tunggal. Untuk pasangan data teks imej 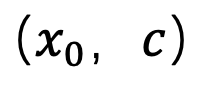 , kaedah ini melatih Unet
, kaedah ini melatih Unet 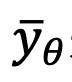 agar muat
agar muat 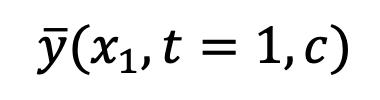 . Fungsi kehilangan dinyatakan sebagai:
. Fungsi kehilangan dinyatakan sebagai: 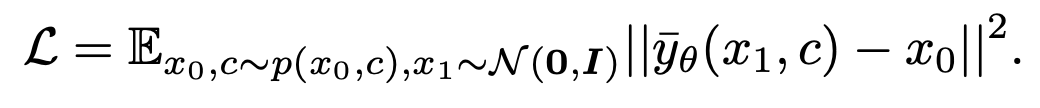
Selepas model telah menumpu, anda boleh mengikuti formula pensampelan DDIM di bawah dan menggunakan modul yang baru diperolehi  pensampelan
pensampelan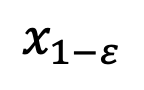 .
. 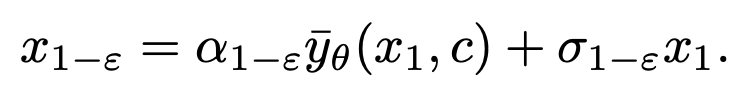
Formula pensampelan DDIM memastikan  yang dihasilkan mematuhi pengedaran data
yang dihasilkan mematuhi pengedaran data 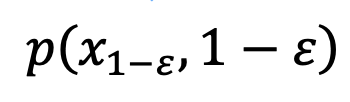 pada saat 1-ε, dengan itu menyelesaikan masalah skala kelabu purata. Selepas langkah ini, model pralatihan boleh digunakan untuk melaksanakan langkah persampelan seterusnya sehingga
pada saat 1-ε, dengan itu menyelesaikan masalah skala kelabu purata. Selepas langkah ini, model pralatihan boleh digunakan untuk melaksanakan langkah persampelan seterusnya sehingga 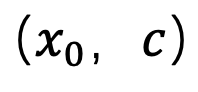 dijana. Perlu diingat bahawa memandangkan kaedah ini hanya mengambil bahagian dalam langkah pertama persampelan dan tiada kaitan dengan proses persampelan seterusnya, SingDiffusion boleh digunakan untuk kebanyakan model resapan sedia ada. Di samping itu, untuk mengelakkan masalah limpahan data yang disebabkan oleh operasi tanpa bimbingan pengelas, kaedah ini juga menggunakan operasi normalisasi berikut:
dijana. Perlu diingat bahawa memandangkan kaedah ini hanya mengambil bahagian dalam langkah pertama persampelan dan tiada kaitan dengan proses persampelan seterusnya, SingDiffusion boleh digunakan untuk kebanyakan model resapan sedia ada. Di samping itu, untuk mengelakkan masalah limpahan data yang disebabkan oleh operasi tanpa bimbingan pengelas, kaedah ini juga menggunakan operasi normalisasi berikut: 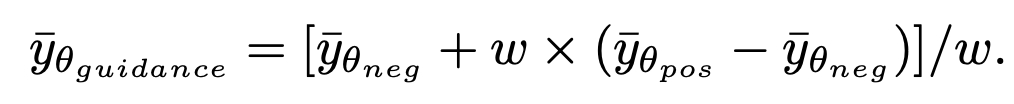
di mana panduan mewakili hasil selepas operasi tanpa bimbingan pengelas, dan neg mewakili hasilnya. di bawah gesaan negatif Output, pos mewakili output di bawah gesaan positif, dan ω mewakili keamatan panduan. Pertama, kajian itu mengesahkan keupayaan SingDiffusion untuk menyelesaikan masalah skala kelabu purata pada tiga model: SD-1.5, SD-2.0-asas dan SD-2.0. Kajian ini memilih empat gesaan melampau, termasuk "latar belakang putih/hitam tulen" dan "logo seni garis monokrom pada latar belakang putih/hitam", sebagai syarat untuk penjanaan dan mengira purata nilai skala kelabu bagi imej yang dijana, seperti yang ditunjukkan dalam jadual di bawah Ditunjukkan: 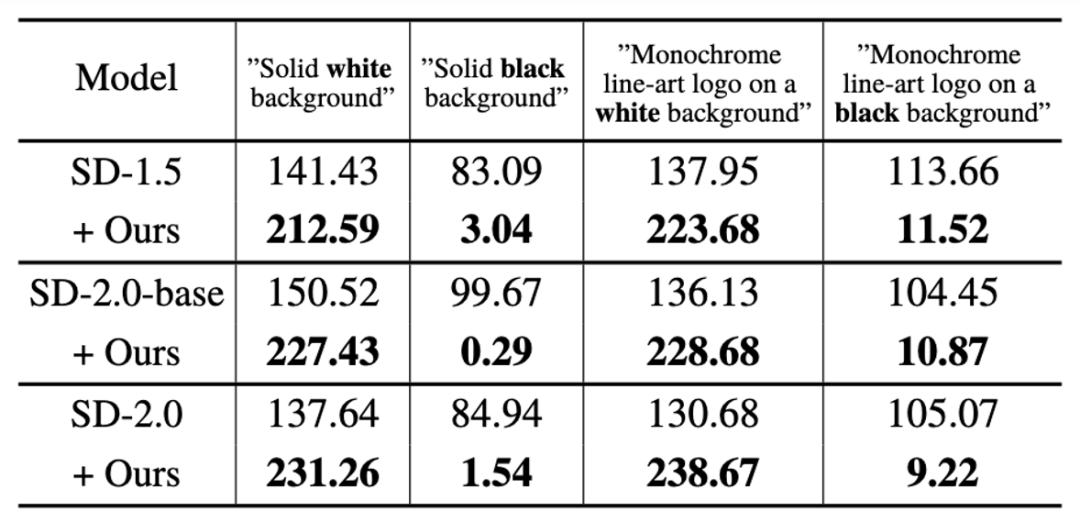
Seperti yang dapat dilihat daripada jadual, penyelidikan ini dapat menyelesaikan masalah purata nilai kelabu dengan ketara dan menjana imej yang sepadan dengan kecerahan penerangan teks input. Di samping itu, kajian itu juga menggambarkan hasil penjanaan di bawah empat pernyataan segera ini, seperti yang ditunjukkan dalam rajah di bawah: 
Seperti yang dapat dilihat daripada rajah, selepas menambah kaedah ini, model resapan sedia ada boleh menjana hitam atau Putih gambar. Untuk mengkaji lebih lanjut peningkatan kualiti imej yang dicapai melalui kaedah ini, kajian memilih 30,000 penerangan untuk ujian pada dataset COCO. Pertama sekali, kajian ini menunjukkan keupayaan generatif model itu sendiri tanpa menggunakan panduan bebas pengelas, seperti yang ditunjukkan dalam jadual berikut: 
Seperti yang dapat dilihat daripada jadual, kaedah yang dicadangkan boleh mengurangkan FID dengan ketara imej yang dijana, dan menambah baik penunjuk CLIP. Perlu diingat bahawa dalam model SD-1.5, kaedah dalam kertas ini mengurangkan indeks FID sebanyak 33% berbanding model asal. Seterusnya, untuk mengesahkan keupayaan penjanaan kaedah yang dicadangkan tanpa bimbingan pengelas, kajian juga menunjukkan dalam rajah di bawah bahawa di bawah saiz bimbingan yang berbeza ω∈[1.5,2,3,4,5,6, 7,8] Keluk Pareto CLIP lwn. FID: 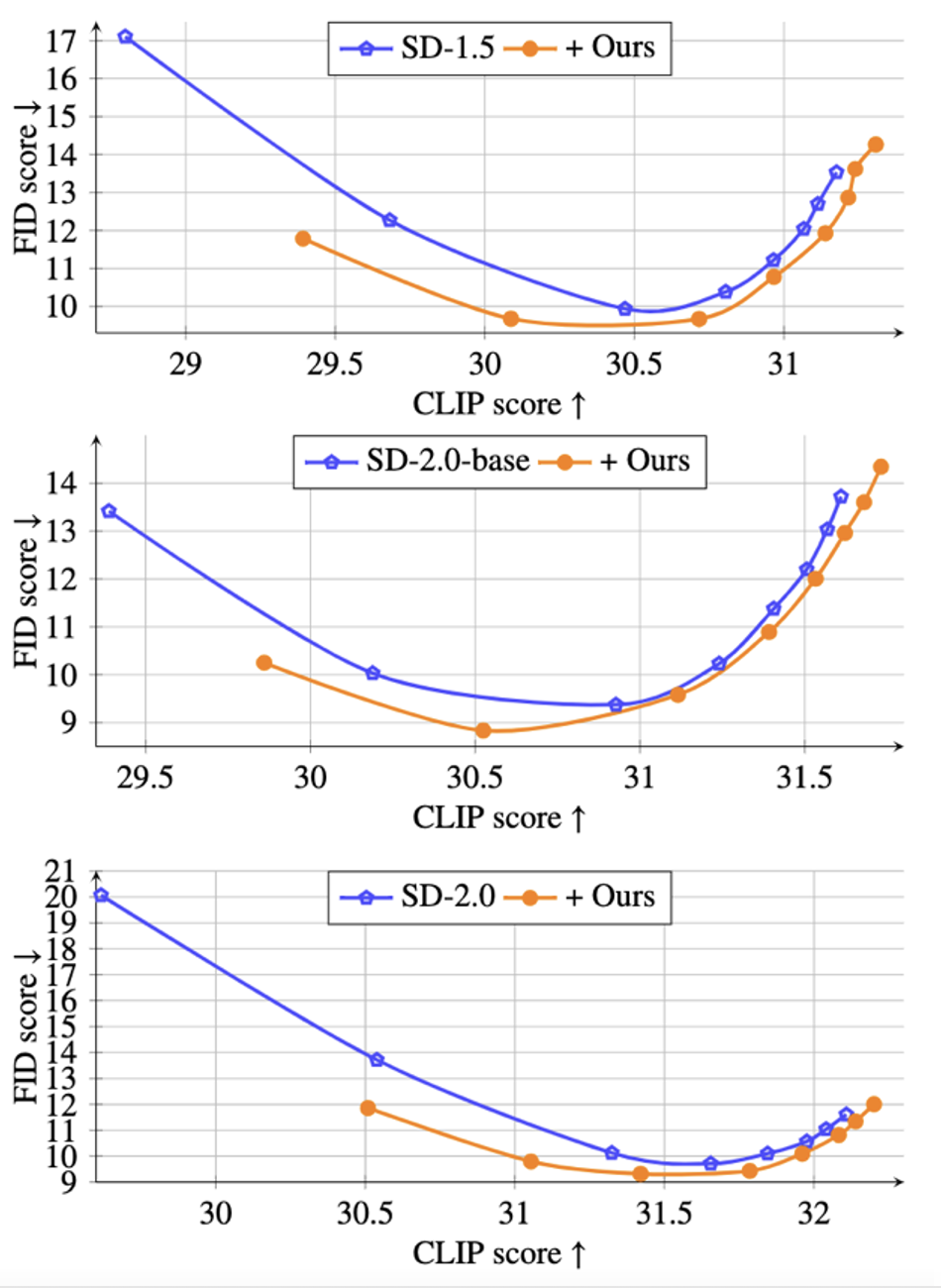
Seperti yang dapat dilihat dari rajah, pada tahap CLIP yang sama, kaedah yang dicadangkan boleh memperoleh nilai FID yang lebih rendah dan menghasilkan imej yang lebih realistik. Selain itu, kajian ini juga menunjukkan keupayaan generalisasi kaedah yang dicadangkan di bawah model pra-latihan CIVITAI yang berbeza, seperti yang ditunjukkan dalam rajah di bawah: 
Dapat dilihat bahawa kaedah yang dicadangkan dalam kajian ini hanya perlu Selepas satu latihan, ia boleh digunakan dengan mudah pada model resapan sedia ada untuk menyelesaikan masalah tahap kelabu purata.
Akhir sekali, kaedah yang dicadangkan oleh penyelidikan ini juga boleh digunakan dengan lancar pada model ControlNet yang telah terlatih, seperti yang ditunjukkan dalam rajah di bawah: 
Seperti yang dapat dilihat daripada keputusan, kaedah ini boleh menyelesaikan purata dengan berkesan masalah kelabu masalah ijazah ControlNet.
[1] Tero Karras, Miika Aittala, Timo Aila, dan Samuli Laine Menjelaskan ruang reka bentuk model generatif berasaskan penyebaran (IPS) Kemajuan Maklumat Neural 26565–26577, 2022. 3Atas ialah kandungan terperinci CVPR 2024|Tidak dapat menjana imej dengan cahaya yang sangat kuat? Pasukan Wawasan WeChat menyelesaikan masalah ketunggalan model penyebaran dengan berkesan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Alamat projek: https://pangzecheung.github.io/SingDiffusion/
Alamat projek: https://pangzecheung.github.io/SingDiffusion/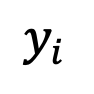 .
.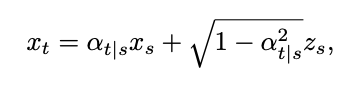
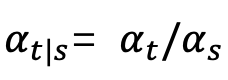 ,
, 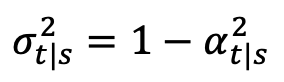 ,
, 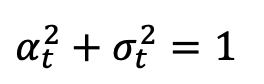 ,
, 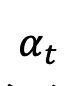 adalah monotonik dengan masa Tukar dari 1 kepada 0. Memandangkan taburan sampel latihan yang baru ditakrifkan, ketumpatan kebarangkalian marginal momen tunggal bagi
adalah monotonik dengan masa Tukar dari 1 kepada 0. Memandangkan taburan sampel latihan yang baru ditakrifkan, ketumpatan kebarangkalian marginal momen tunggal bagi 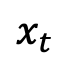 boleh dinyatakan sebagai:
boleh dinyatakan sebagai: 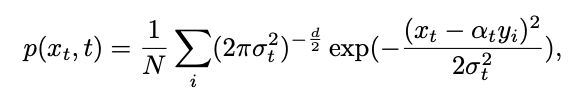
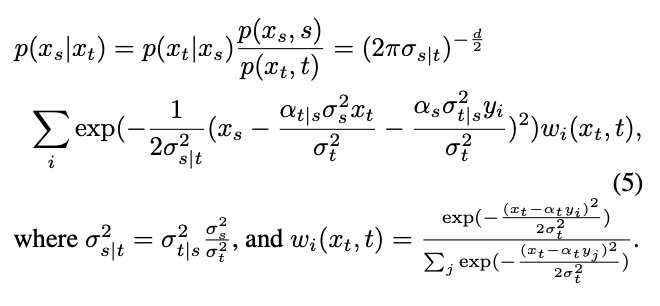
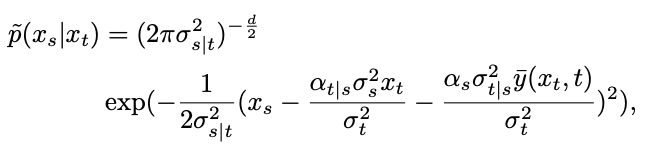
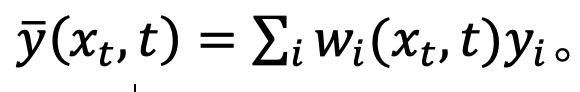 Untuk menguji hipotesis ini, kajian menganggarkan ralat kesesuaian ini dalam Proposisi 1.
Untuk menguji hipotesis ini, kajian menganggarkan ralat kesesuaian ini dalam Proposisi 1. 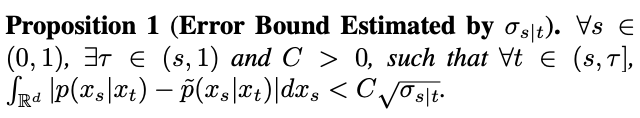
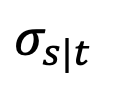 juga akan menghampiri 1, dan ralat itu tidak boleh diabaikan. Oleh itu, Proposisi 1 tidak membuktikan sifat Gaussian songsang pada t=1. Untuk menyelesaikan masalah ini, kajian ini memberikan cadangan baru:
juga akan menghampiri 1, dan ralat itu tidak boleh diabaikan. Oleh itu, Proposisi 1 tidak membuktikan sifat Gaussian songsang pada t=1. Untuk menyelesaikan masalah ini, kajian ini memberikan cadangan baru: 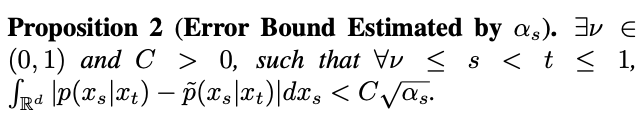
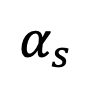 akan menghampiri 0. Oleh itu, kajian ini membuktikan bahawa keseluruhan proses songsang termasuk momen singulariti menepati ciri Gaussian.
akan menghampiri 0. Oleh itu, kajian ini membuktikan bahawa keseluruhan proses songsang termasuk momen singulariti menepati ciri Gaussian.  =0, formula pensampelan berikut akan mempunyai penyebut dibahagikan dengan 0:
=0, formula pensampelan berikut akan mempunyai penyebut dibahagikan dengan 0: 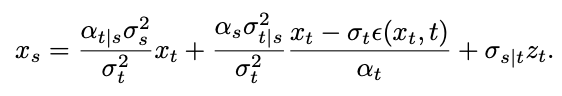
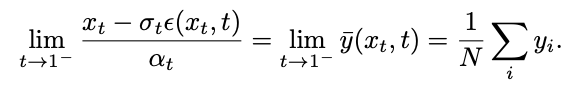
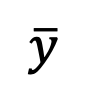 pada masa t=1 dan menggunakan "ramalan-x" untuk menyelesaikan masalah pensampelan pada titik tunggal awal.
pada masa t=1 dan menggunakan "ramalan-x" untuk menyelesaikan masalah pensampelan pada titik tunggal awal. 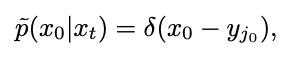
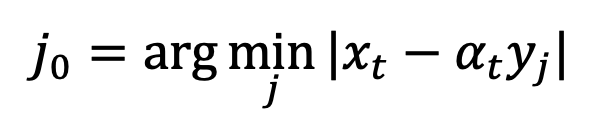 . Singulariti sedemikian akan menyebabkan proses pensampelan menumpu kepada data yang betul
. Singulariti sedemikian akan menyebabkan proses pensampelan menumpu kepada data yang betul 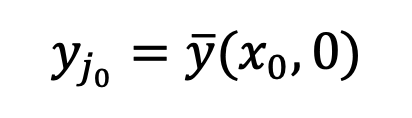 . Oleh itu, ketunggalan pada t=0 adalah sifat yang baik bagi model resapan dan tidak perlu dielakkan.
. Oleh itu, ketunggalan pada t=0 adalah sifat yang baik bagi model resapan dan tidak perlu dielakkan. 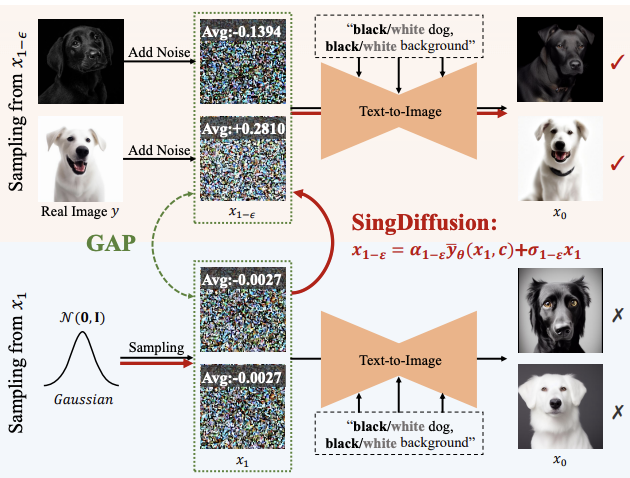
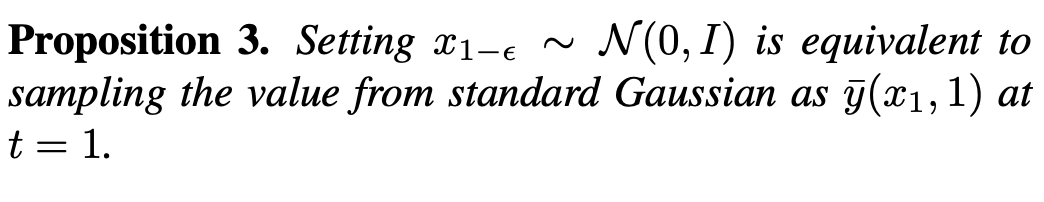

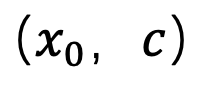 , kaedah ini melatih Unet
, kaedah ini melatih Unet 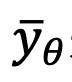 agar muat
agar muat 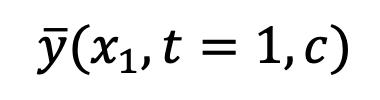 . Fungsi kehilangan dinyatakan sebagai:
. Fungsi kehilangan dinyatakan sebagai: 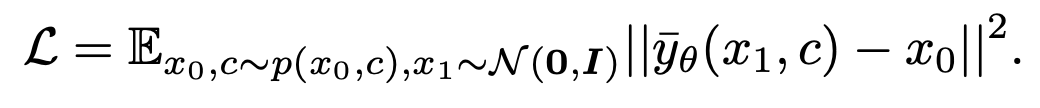
 pensampelan
pensampelan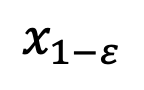 .
. 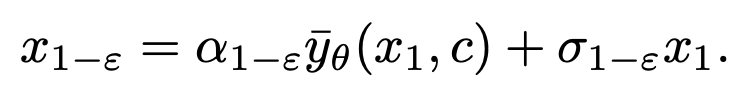
 yang dihasilkan mematuhi pengedaran data
yang dihasilkan mematuhi pengedaran data 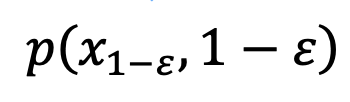 pada saat 1-ε, dengan itu menyelesaikan masalah skala kelabu purata. Selepas langkah ini, model pralatihan boleh digunakan untuk melaksanakan langkah persampelan seterusnya sehingga
pada saat 1-ε, dengan itu menyelesaikan masalah skala kelabu purata. Selepas langkah ini, model pralatihan boleh digunakan untuk melaksanakan langkah persampelan seterusnya sehingga 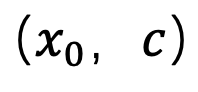 dijana. Perlu diingat bahawa memandangkan kaedah ini hanya mengambil bahagian dalam langkah pertama persampelan dan tiada kaitan dengan proses persampelan seterusnya, SingDiffusion boleh digunakan untuk kebanyakan model resapan sedia ada. Di samping itu, untuk mengelakkan masalah limpahan data yang disebabkan oleh operasi tanpa bimbingan pengelas, kaedah ini juga menggunakan operasi normalisasi berikut:
dijana. Perlu diingat bahawa memandangkan kaedah ini hanya mengambil bahagian dalam langkah pertama persampelan dan tiada kaitan dengan proses persampelan seterusnya, SingDiffusion boleh digunakan untuk kebanyakan model resapan sedia ada. Di samping itu, untuk mengelakkan masalah limpahan data yang disebabkan oleh operasi tanpa bimbingan pengelas, kaedah ini juga menggunakan operasi normalisasi berikut: