PHP速学视频免费教程(入门到精通)
PHP怎么学习?PHP怎么入门?PHP在哪学?PHP怎么学才快?不用担心,这里为大家提供了PHP速学教程(入门到精通),有需要的小伙伴保存下载就能学习啦!
这项工作代表了 AI 在数学推理上的能力突破,是开发通用 AI 系统方面的重要里程碑。
这一次,人工智能算法在数学奥林匹克竞赛(imo)上取得了重大成绩突破。

在最新一期的国际权威期刊《自然》杂志上,发表了一篇论文介绍了名为AlphaGeometry的人工智能系统。该系统能够解决奥林匹克几何问题,而无需人类的示范。专家认为,这是人工智能朝着具备人类推理能力的方向迈进的重要里程碑。这项研究成果的发表对于推动人工智能的进一步发展具有重要意义。

论文链接:https://www.nature.com/articles/s41586-023-06747-5
DeepMind 也在论文发表的第一时间将代码和模型开源,GitHub:https://github.com/google-deepmind/alphageometry
这是一种人工智能系统,来自 Google DeepMind 研究者之手,它能够以接近人类奥赛金牌得主的水平解决复杂的几何问题。
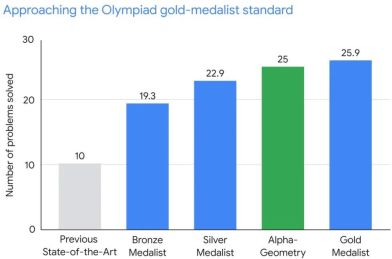
在对30道奥数几何题的基准测试中,AlphaGeometry在标准奥数时限内解决了25道题,而之前最先进的系统只解决了其中10道几何问题。与此相比,人类金牌得主的平均解决问题数量为25.9个。
对于基于学习的AI模型来说,定理证明是一项具有挑战性的任务。主要原因在于,大多数数学领域中的人类证明很难被翻译成机器可验证的语言,从而限制了用于训练AI模型的数据量。为了克服这一问题,DeepMind提出了一种替代方法,即使用合成数据进行定理证明。他们开发了一个通用的指导框架,称为AlphaGeometry,该框架在许多领域都具有适用性。通过利用合成数据,AlphaGeometry能够训练AI模型进行定理证明,并产生高质量的结果。这一方法为解决定理证明的困难提供了一种有效的解决方案。
研究介绍
AlphaGeometry 将语言模型与「符号引擎」相结合,借助符号和逻辑规则进行数学推论。在这其中,语言模型擅长识别、预测流程的后续步骤,但缺乏数学推理所需的严谨性;另一方面,符号引擎纯粹基于形式逻辑和严格的规则,这使得它能够引导语言模型走向理性决策。
在 AlphaGeometry 的研究上,DeepMind 从跨越 2000 年到 2022 年之间的 30 个奥林匹克几何问题(IMO-AG-30)的基准测试集中进行了测试,结果表明,AlphaGeometry 在比赛时间限制下能够解决 25 个问题。而之前最先进的方法(Wu’s method)只能解决 10 个。
众所周知,由于缺乏推理技能和训练数据,AI 系统经常难以解决几何和数学方面的复杂问题。AlphaGeometry 系统将神经语言模型的预测能力与规则约束推理引擎相结合,两者协同工作以找到了新的解决方案。
此外,为了解决数据难题,该研究生成了大量的合成训练数据,即 1 亿个示例,其中许多定理的证明步骤超过 200 步,比数学奥林匹克竞赛定理的平均证明长度长 4 倍。
AlphaGeometry 展示了 AI 不断增长的逻辑推理能力以及发现和验证新知识的能力。解决奥林匹克级别的几何问题是 AI 在迈向更先进和通用人工智能系统道路上的一个重要里程碑。
菲尔兹奖得主、IMO 金牌获得者 Ngô Bảo Châu(吴宝珠)表示:「现在我完全明白了,为什么 AI 研究者们会首先尝试解决国际数学奥林匹克 (IMO) 的几何题目,因为找到它们的解决方案有点像下棋,我们在每一步都有相对较少的合理走法。但我仍然对他们能够实现这一点感到震惊。这是一项令人印象深刻的成就。」

吴宝珠,2010 年菲尔兹奖得主,现任芝加哥大学教授。
AlphaGeometry 是一个神经符号系统,由神经语言模型和符号推演引擎组成,它们共同寻找复杂几何定理的证明。一个系统提供快速、直观的想法,而另一种则提供更加深思熟虑、理性的决策。
由于语言模型擅长识别数据中的一般模式和关系,因此它们可以快速预测潜在有用的结构,但通常缺乏严格推理或做出解释。另一方面,符号推演引擎基于形式逻辑并使用明确的规则来得出结论,两者相互配合,共同构成了 AlphaGeometry。
AlphaGeometry 的语言模型引导其符号推演引擎寻找几何问题的可能解决方案。一般的奥林匹克几何问题基于图表,需要添加新的几何结构才能解决,例如点、线或圆。AlphaGeometry 的语言模型可以从无数种可能性中预测添加哪些新结构最有用。这些线索有助于填补空白,并允许符号引擎对图表进行进一步推论并接近解决方案。
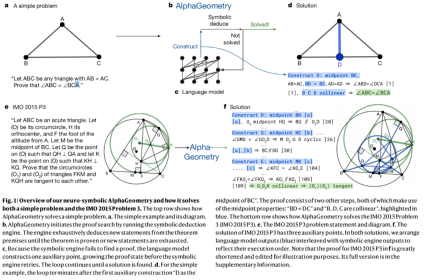
举例来说,下图(上)为 AlphaGeometry 解答简单题的过程,题目为「设 ABC 为 AB = AC 的任意三角形。证明∠ABC = ∠BCA。」
AlphaGeometry 证明过程是这样的:AlphaGeometry 通过运行符号推演引擎(symbolic deduction engine)启动证明搜索。这个引擎会从定理的前提出发,详尽地推导出新的陈述,直到定理得到证明或者新的陈述被耗尽。假如符号引擎未能找到证明,语言模型会构造一个辅助点,在符号引擎重新开始之前增加可证明的条件。这个循环一直持续到找到解决方案为止。对于简单的例子,循环在第一个辅助结构「 BC 的中点添加 D 点」之后终止。
下图(下)为 AlphaGeometry 解决 IMO 的解题思路。「证明三角形 FKM 和 KQH 的外接圆 (O1) 和 (O2) 彼此相切……」,这么复杂的问题,AlphaGeometry 同样也能证明,证明过程还给出了辅助点等。出于说明目的,证明过程被大大缩短和编辑。
生成 1 亿数学推理训练数据
人类可以在纸上进行勾画来学习几何、检查图表并使用现有知识来发现新的、更复杂的几何属性和关系。该研究生成合成数据的方法大规模模拟了这种知识构建过程。其中生成合成数据的方法如图 3 所示。

使用高度并行计算,系统首先生成 5 亿个几何对象的随机图,并详尽地导出每个图中点和线之间的所有关系。AlphaGeometry 找到每个图中包含的所有证明,然后逆向推导,找出需要哪些额外的结构(如果有的话)来获得这些证明。这一过程为「符号推演与回溯」。

由 AlphaGeometry 生成的合成数据的可视化表示
之后,这个巨大的数据池被过滤以排除类似的示例,从而产生了 1 亿个训练数据集。
开创性的人工智能推理能力
AlphaGeometry 提供的每一道奥数题的解法都经过计算机检查和验证。研究人员还将其结果与之前的人工智能方法以及人类在奥林匹克竞赛中的表现进行了比较。此外,数学教练、前奥赛金牌得主 Evan Chen(陈谊廷)为我们评估了 AlphaGeometry 的一系列解决方案。

陈谊廷,MIT 数学在读博士,曾获得 IMO 2014 年金牌。
Evan Chen 表示:「AlphaGeometry 的输出令人印象深刻,因为它既可验证又干净。过去针对基于证明的竞争问题的人工智能解决方案有时是碰巧的(输出有时是正确的,需要人工检查),而 AlphaGeometry 没有这个弱点:它的解决方案具有机器可验证的结构。另一方面,它的输出仍然是人类可读的。人们可以想象一个通过强力坐标系解决几何问题的计算机程序:想想一页又一页繁琐的代数计算,AlphaGeometry 不是这样做的,它像人类学生一样使用带有角度和相似三角形的经典几何规则。」
最近一段时间,金融科技公司 XTX Markets 设立了人工智能奥林匹克数学奖(AI-MO Prize),旨在鼓励能够进行数学推理的人工智能模型的开发。由于每个奥林匹克竞赛都有六个问题,其中只有两个通常集中在几何上,因此 AlphaGeometry 只能应用于给定奥林匹克竞赛中的三分之一问题。
尽管如此,AlphaGeometry 仅靠自己的几何解题能力就成为了世界上第一个能够在 2000 年和 2015 年通过 IMO 铜牌门槛的人工智能模型。
DeepMind 已在着手推进下一代人工智能系统的推理。研究人员认为,鉴于利用大规模合成数据从头开始训练人工智能系统的广泛潜力,这种方法可能会影响未来人工智能系统发现数学及其他领域新知识的方向。
AlphaGeometry 开创了人工智能数学推理的先河 —— 从探索纯数学之美到使用语言模型解决数学和科学问题。人们希望这种技术能够继续提升,进而解决更高级、抽象的数学问题。
而在数学之外,AlphaGeometry 的影响或许还可以覆盖到包含几何问题的更多领域,如计算机视觉、建筑,甚至理论物理学等。
参考内容:
https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/

已抢6799个
抢
已抢91611个
抢
已抢14418个
抢
已抢50597个
抢
已抢190557个
抢
已抢86253个
抢