Model kuantitatif pengkomputeran selari dan aplikasinya dalam enjin pembelajaran mendalam

Satu-satunya seni mempertahankan diri di dunia yang tidak boleh dikalahkan ialah kepantasan. Cara melatih model pembelajaran mendalam dengan lebih pantas sentiasa menjadi tumpuan industri sama ada membangunkan perkakasan khas atau membangunkan rangka kerja perisian, masing-masing menunjukkan kebolehan mereka yang unik.

Sudah tentu, undang-undang ini boleh dilihat dalam buku teks dan kesusasteraan seni bina komputer, seperti "Seni Bina Komputer: Pendekatan Kuantatif" ini, tetapi nilai artikel ini terletak pada Pilih undang-undang paling asas dalam cara yang disasarkan. dan menggabungkannya dengan enjin pembelajaran yang mendalam untuk memahaminya.

1 Andaian tentang jumlah pengiraan

Sebelum mengkaji model kuantitatif pengkomputeran selari, kami mula-mula membuat beberapa tetapan. Untuk tugas latihan model pembelajaran mendalam yang khusus, dengan mengandaikan bahawa jumlah pengiraan V adalah tetap, secara kasar boleh dianggap bahawa selagi pengiraan magnitud V selesai, model pembelajaran mendalam akan melengkapkan latihan.

Halaman GitHub ini (https://github.com/albanie/convnet-burden) menyenaraikan jumlah pengiraan yang diperlukan oleh model CNN biasa untuk memproses imej Perlu diingat bahawa perkara yang disenaraikan pada halaman ini ialah Jumlah pengiraan dalam fasa ke hadapan memerlukan pengiraan dalam fasa ke belakang semasa fasa latihan Biasanya, jumlah pengiraan dalam fasa ke belakang adalah lebih besar daripada jumlah pengiraan ke hadapan. Kertas ini ( https://openreview.net/pdf?id=Bygq-H9eg ) memberikan hasil visualisasi intuitif bagi jumlah pengiraan pemprosesan imej dalam peringkat latihan:

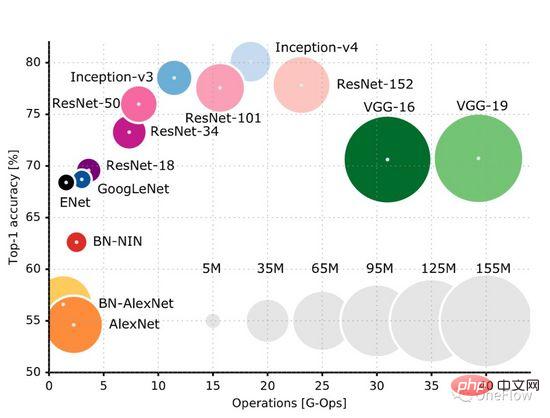
Ambil ResNet-50 sebagai contoh Dalam fasa latihan, pemprosesan imej 224X224x3 memerlukan 8G-Ops (kira-kira 8 bilion pengiraan keseluruhan set data ImageNet mempunyai kira-kira 1.2 juta imej keseluruhan set data. Epochs, anggaran kasar, proses latihan memerlukan sejumlah (8*10^9) *(1.2*10^6)* 90 = 0.864*10^18 operasi, kemudian jumlah pengiraan ResNet -50 proses latihan adalah kira-kira Satu bilion kali satu bilion operasi, kita hanya boleh berfikir bahawa selagi pengiraan ini selesai, operasi model selesai. Matlamat enjin pengkomputeran pembelajaran mendalam adalah untuk melengkapkan jumlah pengiraan yang diberikan ini dalam masa yang paling singkat.

2 Andaian tentang peranti pengkomputeran

Artikel ini terhad kepada peranti pengkomputeran berpusat pemproses (Pengkomputeran berpusat pemproses) yang ditunjukkan dalam rajah di bawah, dan pengkomputeran berpusatkan memori (Memproses dalam memori ) peranti sedang diterokai dalam industri, tetapi ia belum lagi menjadi arus perdana.

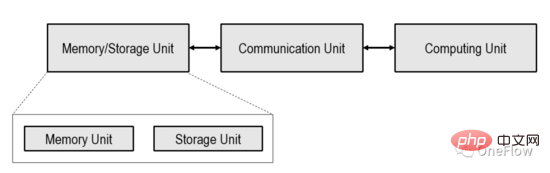
Unit Pengkomputeran dalam peranti pengkomputeran yang ditunjukkan di atas boleh menjadi pemproses tujuan umum seperti CPU, GPGPU atau cip tujuan khas seperti TPU, dsb. Jika Unit Pengkomputeran adalah cip tujuan umum, biasanya program dan data disimpan dalam Unit Memori, yang juga merupakan komputer struktur von Neumann yang paling popular hari ini.

Jika Unit Pengkomputeran adalah cip khusus, biasanya hanya data disimpan dalam Unit Memori. Unit Komunikasi bertanggungjawab untuk memindahkan data dari Unit Memori ke Unit Pengkomputeran dan melengkapkan pemuatan data Selepas Unit Pengkomputeran mendapat data, ia bertanggungjawab untuk menyelesaikan pengiraan (penukaran bentuk data kemudiannya memindahkan keputusan pengiraan kepada Unit Memori untuk melengkapkan penyimpanan data (Stor).

Keupayaan penghantaran Unit Komunikasi biasanya dinyatakan oleh jalur lebar akses memori beta, iaitu bilangan bait yang boleh dipindahkan sesaat, yang biasanya berkaitan dengan bilangan kabel dan kekerapan isyarat. Kuasa pengkomputeran Unit Pengkomputeran biasanya diwakili oleh pi kadar pemprosesan, iaitu bilangan pengiraan titik terapung (flop) yang boleh diselesaikan sesaat Ini biasanya berkaitan dengan bilangan peranti pengkomputeran logik yang disepadukan pada pengkomputeran unit dan kekerapan jam.

Matlamat enjin pembelajaran mendalam adalah untuk memaksimumkan keupayaan pemprosesan data peranti pengkomputeran melalui reka bentuk bersama perisian dan perkakasan, iaitu, untuk menyelesaikan jumlah pengiraan tertentu dalam masa yang paling singkat.

3 Model Garis Bumbung: Model matematik yang menggambarkan prestasi pengkomputeran sebenar

Prestasi pengkomputeran sebenar (bilangan operasi selesai sesaat) yang boleh dicapai oleh peranti pengkomputeran apabila melaksanakan tugas bukan sahaja berkaitan kepada jalur lebar capaian memori Beta berkaitan dengan pi puncak teori bagi unit pengkomputeran, dan juga dengan keamatan operasi (Keamatan aritmetik, atau Keamatan Operasi) tugas semasa itu sendiri.

Keamatan pengkomputeran tugas ditakrifkan sebagai bilangan pengiraan titik terapung yang diperlukan bagi setiap bait data, iaitu Flop setiap bait. Difahamkan secara umum, tugas dengan intensiti pengiraan yang rendah bermakna Unit Pengkomputeran perlu melakukan lebih sedikit operasi pada bait yang diangkut oleh Unit Komunikasi Untuk memastikan Unit Pengkomputeran sibuk dalam kes ini, Unit Komunikasi mesti kerap mengangkut data >

Tugas dengan intensiti pengiraan yang tinggi bermakna Unit Pengkomputeran perlu melakukan lebih banyak operasi pada bait yang dipindahkan oleh Unit Komunikasi Unit Komunikasi tidak perlu memindahkan data dengan begitu kerap untuk memastikan Unit Pengkomputeran sibuk.

Pertama sekali, prestasi pengkomputeran sebenar tidak akan melebihi pi puncak teori unit pengkomputeran. Kedua, jika beta jalur lebar akses memori adalah sangat kecil, hanya bait beta boleh dipindahkan dari memori ke Unit Pengkomputeran dalam 1 saat Biarkan saya mewakili bilangan operasi yang diperlukan untuk setiap bait dalam tugas pengkomputeran semasa, kemudian beta * I mewakili 1 saat. Bilangan sebenar operasi yang diperlukan untuk memindahkan data dalam satu jam Jika beta * I

Model garis bumbung ialah model matematik yang menyimpulkan prestasi pengkomputeran sebenar berdasarkan hubungan antara lebar jalur akses memori, kadar daya pemprosesan puncak unit pengkomputeran dan keamatan pengkomputeran tugas. Diterbitkan oleh pasukan David Patterson di Communications of ACM pada tahun 2008 ( https://en.wikipedia.org/wiki/Roofline_model ), ia adalah model visual yang ringkas dan elegan:

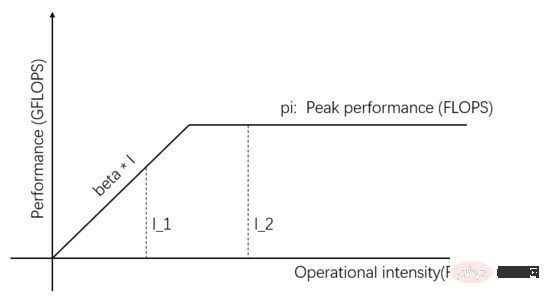
Rajah 1: Model Garis Bumbung

Pembolehubah tidak bersandar pada paksi mendatar Rajah 1 mewakili keamatan pengkomputeran tugas yang berbeza, iaitu bilangan operasi titik terapung yang diperlukan setiap bait. Pembolehubah bersandar pada paksi menegak mewakili prestasi pengkomputeran sebenar yang boleh dicapai, iaitu bilangan operasi titik terapung yang dilakukan sesaat. Angka di atas menunjukkan prestasi pengkomputeran sebenar yang boleh dicapai dengan dua tugasan dengan keamatan pengkomputeran I_1 dan I_2 Keamatan pengkomputeran I_1 adalah kurang daripada pi/beta, yang dipanggil tugas terhad akses ingatan prestasi pengkomputeran sebenar beta * I_1 adalah lebih rendah daripada pi puncak teori.

Keamatan pengkomputeran I_2 adalah lebih tinggi daripada pi/beta, yang dipanggil tugasan terhad pengkomputeran Prestasi pengkomputeran sebenar mencapai pi puncak teori, dan lebar jalur akses memori hanya menggunakan pi/(I_2*beta. ). Kecerunan cerun dalam rajah ialah beta Persilangan cerun dan garis mendatar puncak teori dipanggil titik rabung Absis titik rabung ialah pi/beta Apabila keamatan pengiraan tugasan pi/beta, Unit Komunikasi Ia berada dalam keadaan seimbang dengan Unit Pengkomputeran, dan tiada satu pun yang sia-sia.

Mengingat bahawa matlamat enjin pembelajaran mendalam adalah untuk "menyelesaikan jumlah pengiraan tertentu dalam masa yang paling singkat", adalah perlu untuk memaksimumkan prestasi pengkomputeran sebenar sistem yang boleh dicapai. Untuk mencapai matlamat ini, beberapa strategi disediakan.

I_2 dalam Rajah 1 ialah tugas terhad pengkomputeran prestasi pengkomputeran sebenar boleh dipertingkatkan dengan meningkatkan keselarian Unit Pengkomputeran dan dengan itu meningkatkan nilai puncak teori Contohnya, menyepadukan lebih banyak unit logik pengkomputeran Unit (ALU). Khusus kepada senario pembelajaran mendalam, ini bermakna menambah GPU, daripada satu GPU kepada beberapa GPU yang beroperasi pada masa yang sama.

Seperti yang ditunjukkan dalam Rajah 2, apabila lebih banyak selari ditambah dalam Unit Pengkomputeran, nilai puncak teori adalah lebih tinggi daripada beta * I_2, maka prestasi pengkomputeran sebenar I_2 adalah lebih tinggi, dan ia hanya mengambil masa yang lebih singkat boleh.

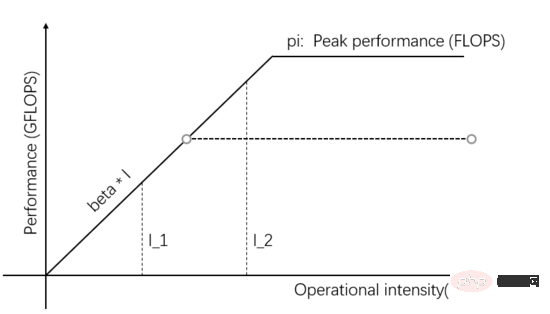
Rajah 2: Menambah baik nilai puncak teori Unit Pengkomputeran untuk meningkatkan prestasi pengkomputeran sebenar

I_1 dalam Rajah 1 ialah tugas terhad akses memori, maka Prestasi pengkomputeran sebenar dan keupayaan bekalan data boleh dipertingkatkan dengan menambah baik jalur lebar penghantaran Unit Komunikasi. Seperti yang ditunjukkan dalam Rajah 3, cerun cerun mewakili lebar jalur penghantaran Unit Komunikasi Apabila cerun cerun meningkat, I_1 berubah daripada tugas terhad akses memori kepada tugas terhad pengiraan, dan prestasi pengkomputeran sebenar adalah. bertambah baik.

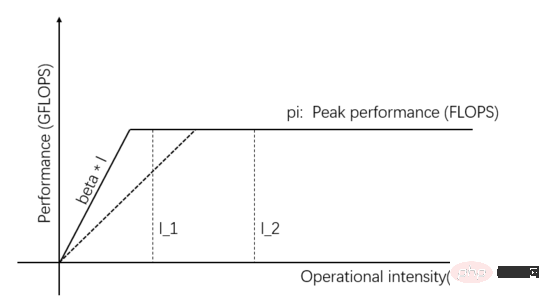
Rajah 3: Meningkatkan kapasiti bekalan data Unit Komunikasi untuk meningkatkan prestasi pengkomputeran sebenar

Selain meningkatkan prestasi pengkomputeran sebenar dengan menambah baik penghantaran lebar jalur atau puncak teori perkakasan Selain prestasi, prestasi pengkomputeran sebenar juga boleh dipertingkatkan dengan menambah baik keamatan pengkomputeran tugas itu sendiri. Tugas yang sama boleh dilaksanakan dalam pelbagai cara yang berbeza, dan keamatan pengkomputeran bagi pelaksanaan yang berbeza juga berbeza. Selepas keamatan pengkomputeran diubah daripada I_1 kepada melebihi pi/beta, ia menjadi tugas terhad pengkomputeran, dan prestasi pengkomputeran sebenar mencapai pi, melebihi beta asal*I_1.

Dalam enjin pembelajaran mendalam sebenar, ketiga-tiga kaedah di atas (meningkatkan selari, meningkatkan lebar jalur penghantaran dan menggunakan algoritma dengan keamatan pengiraan yang lebih baik) semuanya digunakan.

4 Hukum Amdahl: Bagaimana untuk mengira nisbah kelajuan?

Contoh dalam Rajah 2 meningkatkan prestasi pengkomputeran sebenar dengan meningkatkan keselarian Unit Pengkomputeran Berapa lama masa pelaksanaan tugas boleh dipendekkan? Ini adalah isu nisbah pecutan, iaitu kecekapan meningkat beberapa kali.

Untuk kemudahan perbincangan, (1) kami menganggap bahawa tugas semasa adalah terhad secara pengiraan, biar saya mewakili keamatan pengkomputeran, iaitu, I*beta>pi. Selepas meningkatkan unit pengkomputeran Unit Pengkomputeran sebanyak s kali, puncak pengkomputeran teori ialah s * pi Anggapkan bahawa keamatan pengkomputeran I tugas adalah cukup tinggi supaya selepas nilai puncak teori dinaikkan sebanyak s kali, ia masih. terhad secara pengiraan, iaitu, I*beta > s*pi; (2) Dengan mengandaikan bahawa tiada saluran paip digunakan, Unit Komunikasi dan Unit Pengkomputeran sentiasa dilaksanakan secara berurutan (kita akan membincangkan kesan saluran paip secara khusus kemudian). Mari kita hitung berapa kali kecekapan pelaksanaan tugas telah bertambah baik.

Dalam situasi awal di mana nilai puncak teori ialah pi, Unit Komunikasi memindahkan beta bait data dalam 1 saat, dan Unit Pengkomputeran memerlukan (I*beta)/pi saat untuk melengkapkan pengiraan. Iaitu, pengiraan I*beta diselesaikan dalam masa 1+(I*beta)/pi saat, maka pengiraan (I*beta) / (1 + (I*beta)/pi) boleh diselesaikan setiap unit masa , dengan mengandaikan bahawa jumlah Jumlah pengiraan ialah V, jadi ia mengambil masa t1=V*(1+(I*beta)/pi)/(I*beta) saat secara keseluruhan.

Selepas meningkatkan puncak pengiraan teori sebanyak s kali dengan meningkatkan selari, Unit Komunikasi masih memerlukan 1 saat untuk memindahkan bait beta data, dan Unit Pengkomputeran memerlukan (I*beta)/(s*pi) saat untuk dikira. Dengan mengandaikan bahawa jumlah pengiraan ialah V, ia mengambil masa t2=V*(1+(I*beta)/(s*pi))/(I*beta) saat untuk menyelesaikan tugasan.

Kira t1/t2 untuk mendapatkan nisbah pecutan: 1/(pi/(pi+I*beta)+(I*beta)/(s*(pi+I*beta))) Maaf, formula ini ialah hodoh, pembaca boleh mendapatkannya sendiri, yang agak mudah.

Apabila nilai puncak teori ialah pi, ia mengambil masa 1 saat untuk memindahkan data dan (I*beta)/pi saat untuk mengira, maka perkadaran masa pengiraan ialah (I*beta)/(pi + I * beta), kita biarkan p mewakili nisbah ini, sama dengan (I*beta)/(pi + I*beta).

Menggantikan p ke dalam nisbah pecutan t1/t2, anda boleh mendapatkan nisbah pecutan sebagai 1/(1-p+p/s Ini ialah undang-undang Amdahl yang terkenal ( https://ms.wikipedia .org/ wiki/Amdahl%27s_law ). Di mana p mewakili bahagian tugas asal yang boleh disejajarkan, s mewakili gandaan selari, dan 1/(1-p+p/s) mewakili kelajuan yang diperolehi.

Mari kita gunakan pengiraan nombor mudah, andaikan Unit Komunikasi mengambil masa 1 saat untuk memindahkan data dan Unit Pengkomputeran mengambil masa 9 saat untuk mengira, kemudian p=0.9. Andaikan bahawa kita meningkatkan keselarian Unit Pengkomputeran dan meningkatkan nilai puncak teorinya sebanyak 3 kali, iaitu, s=3 Kemudian Unit Pengkomputeran hanya mengambil masa 3 saat untuk menyelesaikan pengiraan. Menggunakan undang-undang Amdahl, kita boleh tahu bahawa nisbah pecutan ialah 2.5 kali, dan nisbah pecutan 2.5 adalah kurang daripada gandaan selari 3 Unit Pengkomputeran.

Kami telah merasai kemanisan meningkatkan keselarian Unit Pengkomputeran Bolehkah kami memperoleh nisbah pecutan yang lebih baik dengan meningkatkan lagi keselarian? boleh. Sebagai contoh, jika s=9, maka kita boleh memperoleh nisbah pecutan 5x, dan kita dapat melihat bahawa faedah peningkatan selari semakin kecil.

Bolehkah kita meningkatkan nisbah kelajuan dengan meningkatkan s tanpa terhingga? Ya, tetapi ia semakin kurang kos efektif bayangkan jika s cenderung kepada infiniti (iaitu, jika nilai puncak teori Unit Pengkomputeran adalah tidak terhingga), p/s akan cenderung kepada 0, maka pecutan maksimum. nisbah ialah 1/(1-p)=10.

Selagi terdapat bahagian yang tidak boleh selari (Unit Komunikasi) dalam sistem, nisbah pecutan tidak boleh melebihi 1/(1-p).

Situasi sebenar mungkin lebih teruk daripada had atas nisbah pecutan 1/(1-p), kerana analisis di atas menganggap bahawa keamatan pengkomputeran I adalah tak terhingga, dan apabila meningkatkan keselarian Unit Pengkomputeran, ia biasanya akan menjadikan Unit Komunikasi Apabila lebar jalur penghantaran berkurangan, p menjadi lebih kecil dan 1/(1-p) menjadi lebih besar.

Kesimpulan ini sangat pesimis Walaupun overhed komunikasi (1-p) hanya menyumbang 0.01, ini bermakna tidak kira berapa banyak unit selari digunakan, berpuluh-puluh ribu, kita hanya boleh memperoleh kelajuan maksimum. sebanyak 100 kali. Adakah terdapat sebarang cara untuk membuat p sehampir 1 yang mungkin, iaitu, 1-p menghampiri 0, dengan itu meningkatkan nisbah pecutan? Terdapat peluru ajaib: barisan pemasangan.

5 Pipelining: Panacea

Apabila mendapatkan undang-undang Amdahl, kami menganggap bahawa Unit Komunikasi dan Unit Pengkomputeran berfungsi secara bersiri Unit Komunikasi sentiasa memindahkan data terlebih dahulu, dan Unit Pengkomputeran melakukan pengiraan. Selepas selesai, Unit Komunikasi diminta untuk memindahkan data, dan kemudian mengira semula, dan seterusnya.

Bolehkah Unit Komunikasi dan Unit Pengkomputeran berfungsi pada masa yang sama, memindahkan data dan mengira pada masa yang sama? Jika Unit Pengkomputeran boleh serta-merta mula mengira kumpulan data seterusnya selepas setiap keping data dikira, maka p akan menjadi hampir 1. Tidak kira berapa kali darjah selari s dinaikkan, nisbah pecutan linear boleh diperolehi. Mari kita periksa keadaan di mana kelajuan linear boleh diperolehi.

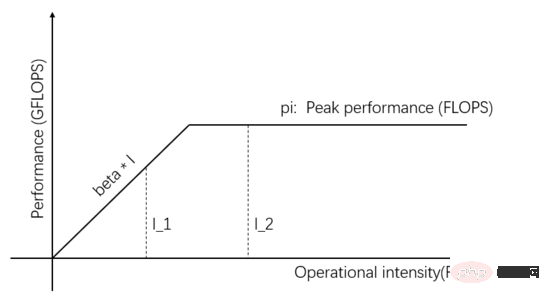
Rajah 4: (Sama seperti Rajah 1) Model Roofline

I_1 dalam Rajah 4 ialah tugas terhad komunikasi, dan Unit Komunikasi boleh mengendalikannya dalam 1 saat Untuk data beta-bait, jumlah pengiraan yang diperlukan oleh Unit Pengkomputeran untuk memproses beta-bait ini ialah operasi beta*I_1 Puncak pengiraan teori ialah pi, dan sejumlah (beta*I_1)/pi saat ialah. diperlukan untuk melengkapkan pengiraan.

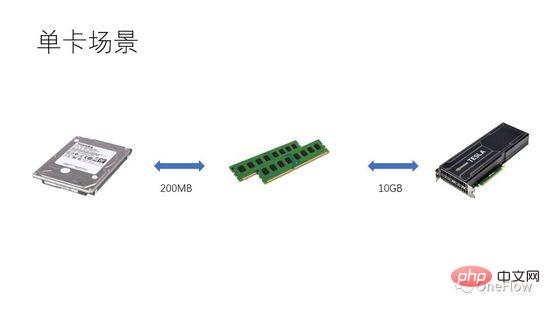
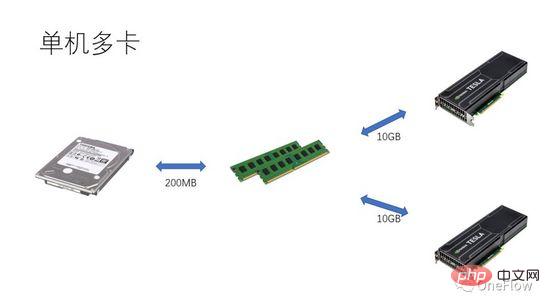
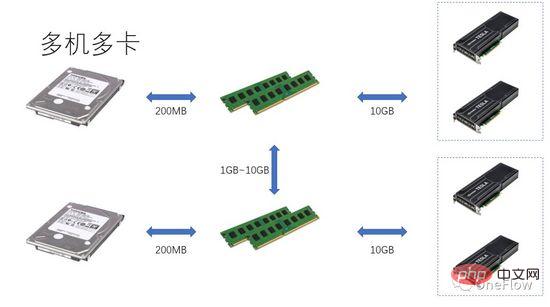
Untuk tugasan terhad komunikasi, kami mempunyai beta*I_1

I_2 dalam Rajah 4 ialah tugasan terhad secara pengiraan Unit Komunikasi boleh memindahkan data bait beta dalam 1 saat Jumlah pengiraan yang diperlukan oleh Unit Pengkomputeran ini ialah operasi beta*I_2 pengiraan Nilai puncak ialah pi, dan ia mengambil masa (beta*I_2)/pi saat untuk melengkapkan pengiraan. Untuk tugasan terhad pengkomputeran, kami mempunyai beta*I_2>pi, jadi masa pengkomputeran Unit Pengkomputeran adalah lebih daripada 1 saat.

Ini juga bermakna mengambil masa beberapa saat untuk menyelesaikan pengiraan data yang mengambil masa 1 saat untuk dipindahkan Terdapat masa yang mencukupi untuk memindahkan kumpulan data seterusnya dalam masa pengiraan, yang bermaksud masa pengiraan boleh ditutup Dari segi masa pemindahan data, p adalah paling banyak 1. Selagi I adalah tak terhingga, nisbah pecutan boleh menjadi tak terhingga.

Teknologi yang membolehkan Unit Komunikasi dan Unit Pengkomputeran berfungsi secara bertindih dipanggil pipelining ( Pipeling: https://en.wikipedia.org/wiki/Pipeline_(computing) ). Ia adalah teknologi yang berkesan meningkatkan penggunaan Unit Pengkomputeran dan meningkatkan nisbah pecutan.

6 Inspirasi model kuantitatif pengkomputeran selari untuk enjin pembelajaran mendalam

Pelbagai model kuantitatif yang dibincangkan di atas juga boleh digunakan untuk pembangunan enjin pembelajaran mendalam Contohnya, untuk tugasan terhad pengkomputeran, anda boleh meningkatkan tahap selari (meningkatkan kad grafik) untuk mempercepatkan walaupun peranti perkakasan yang sama digunakan, menggunakan kaedah selari yang berbeza (keselarian data, model selari atau selari saluran paip) akan menjejaskan keamatan pengkomputeran I, sekali gus menjejaskan prestasi pengkomputeran sebenar ; enjin pembelajaran mendalam yang diedarkan mengandungi sejumlah besar overhed Komunikasi dan overhed masa jalan, cara untuk mengurangkan atau menutup overhed ini adalah penting untuk kesan pecutan.

Memahami model pembelajaran mendalam berdasarkan latihan GPU daripada perspektif peranti pengkomputeran berpusatkan Pemproses, pembaca boleh memikirkan cara mereka bentuk enjin pembelajaran mendalam untuk mendapatkan nisbah pecutan yang lebih baik.

Dalam kes satu mesin dan satu kad, 100% penggunaan GPU boleh dicapai dengan hanya melengkapkan pemindahan data dan saluran pengiraan. Prestasi pengkomputeran sebenar akhirnya bergantung kepada kecekapan pengiraan matriks asas, iaitu, kecekapan cudnn Secara teori, tidak sepatutnya terdapat jurang prestasi antara pelbagai rangka kerja pembelajaran mendalam dalam senario satu kad.

Jika anda ingin memperoleh pecutan dengan menambahkan GPU dalam mesin yang sama, berbanding dengan senario kad tunggal, ini meningkatkan kerumitan pemindahan data antara GPU dan tugasan yang berbeza. Kaedah pembahagian mungkin menghasilkan keamatan pengkomputeran I yang berbeza (contohnya, lapisan konvolusi sesuai untuk keselarian data, dan lapisan bersambung sepenuhnya sesuai untuk keselarian model). Selain overhed komunikasi, overhed penjadualan masa jalan juga mempengaruhi kelajuan.

Dalam senario berbilang mesin dan berbilang kad, kerumitan pemindahan data antara GPU dipertingkatkan lagi Lebar jalur pemindahan data antara mesin melalui rangkaian biasanya lebih rendah daripada bahawa pemindahan data dalam mesin melalui jalur lebar PCIe, yang bermaksud bahawa tahap selari telah meningkat, tetapi jalur lebar pemindahan data telah menurun, yang bermaksud bahawa cerun garisan pepenjuru dalam model Roofline telah menjadi lebih kecil CNN yang sesuai untuk keselarian data biasanya bermaksud keamatan pengkomputeran I yang agak tinggi, dan Terdapat juga beberapa model, seperti RNN/LSTM, yang intensiti pengiraan I adalah jauh lebih kecil, yang juga bermakna bahawa overhed komunikasi dalam saluran paip lebih sukar untuk berselindung.

7 Ringkasan

Pembaca yang telah menggunakan enjin pembelajaran mendalam teragih harus mempunyai pengalaman peribadi tentang nisbah pecutan rangka kerja perisian Pada asasnya, rangkaian saraf konvolusi sesuai untuk keselarian data (intensiti pengkomputeran). Untuk model dengan I yang lebih tinggi), kesan pecutan dengan menambah GPU adalah agak memuaskan Walau bagaimanapun, terdapat kelas besar rangkaian saraf yang menggunakan keselarian model, yang mempunyai keamatan pengiraan yang lebih tinggi sedikit, dan walaupun ia menggunakan keselarian model, ia. keamatan pengiraan masih sangat rendah Ia juga jauh lebih rendah daripada rangkaian saraf konvolusi. Bagaimana untuk mempercepatkan aplikasi ini dengan meningkatkan keselarian GPU adalah masalah yang tidak dapat diselesaikan dalam industri.

Dalam penilaian pembelajaran mendalam sebelum ini, penggunaan berbilang GPU untuk melatih RNN adalah lebih perlahan daripada GPU tunggal ( https://rare-technologies.com/machine-learning-hardware-benchmarks/ ). Tidak kira apa teknologi yang digunakan untuk menyelesaikan masalah kecekapan enjin pembelajaran mendalam, ia tetap sama Untuk meningkatkan nisbah pecutan, semuanya adalah mengenai mengurangkan overhed masa jalan, memilih mod selari yang sesuai untuk meningkatkan keamatan pengkomputeran, dan menutup. komunikasi melalui saluran paip Dalam skop yang diliputi oleh undang-undang asas yang diterangkan dalam artikel ini.

Atas ialah kandungan terperinci Model kuantitatif pengkomputeran selari dan aplikasinya dalam enjin pembelajaran mendalam. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!