Rumah >Peranti teknologi >AI >Ketepatan GPT-3 dalam menyelesaikan masalah matematik telah meningkat kepada 92.5%! Microsoft mencadangkan MathPrompter untuk mencipta model bahasa 'sains' tanpa penalaan halus
Ketepatan GPT-3 dalam menyelesaikan masalah matematik telah meningkat kepada 92.5%! Microsoft mencadangkan MathPrompter untuk mencipta model bahasa 'sains' tanpa penalaan halus
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-12 21:25:011898semak imbas
Kekurangan model bahasa besar yang paling banyak dikritik, selain daripada omong kosong yang serius, mungkin adalah "ketidakupayaan mereka untuk melakukan matematik".
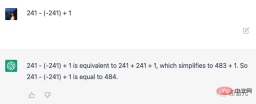
Sebagai contoh, untuk masalah matematik kompleks yang memerlukan penaakulan pelbagai langkah, model bahasa biasanya tidak dapat memberikan yang betul jawapan, walaupun ada Dengan berkat teknologi "rantai berfikir", kesilapan sering berlaku dalam langkah perantaraan.
Berbeza dengan tugas pemahaman bahasa semula jadi dalam seni liberal, soalan matematik biasanya hanya mempunyai satu jawapan yang betul, dan julat jawapan tidak begitu terbuka, menyukarkan tugas menjana penyelesaian yang tepat untuk model bahasa yang besar. Katakan ia lebih mencabar.
Tambahan pula, apabila melibatkan masalah matematik, model bahasa sedia ada biasanya tidak memberikan keyakinan untuk jawapan mereka, menyebabkan pengguna tidak dapat menilai kredibiliti jawapan yang dihasilkan.
Untuk menyelesaikan masalah ini, Microsoft Research mencadangkan teknologi MathPrompter, yang boleh meningkatkan prestasi LLM pada masalah aritmetik sambil meningkatkan pergantungannya pada ramalan.
Pautan kertas: https://arxiv.org/abs/2303.05398
MathPrompter menggunakan pemikiran Zero-shot Teknologi pembayang rantai menjana pelbagai ungkapan algebra atau fungsi Python untuk menyelesaikan masalah matematik yang sama dengan cara yang berbeza, sekali gus meningkatkan kredibiliti hasil keluaran.
Berbanding dengan kaedah CoT berasaskan petunjuk lain, MathPrompter juga menyemak kesahihan langkah perantaraan.
Berdasarkan parameter 175B GPT, kaedah MathPrompter telah digunakan untuk meningkatkan ketepatan set data MultiArith daripada 78.7% kepada 92.5%!
Pengkhususan segera dalam matematik
Dalam beberapa tahun kebelakangan ini, perkembangan pemprosesan bahasa semula jadi sebahagian besarnya dikaitkan dengan pengembangan berterusan dalam skala model bahasa besar (LLM) , yang menunjukkan keupayaan sifar pukulan dan beberapa pukulan yang menakjubkan, dan juga menyumbang kepada pembangunan teknologi dorongan Pengguna hanya perlu memasukkan beberapa contoh mudah ke dalam LLM dengan segera untuk meramalkan tugasan baharu.
prompt boleh dikatakan agak berjaya untuk tugasan satu langkah, tetapi dalam tugas yang memerlukan penaakulan berbilang langkah, prestasi teknologi segera masih tidak mencukupi.
Apabila manusia menyelesaikan masalah yang kompleks, mereka akan memecahkannya dan cuba menyelesaikannya langkah demi langkah Teknologi segera "Chain of Thought" (CoT) meluaskan intuisi ini kepada LLM , peningkatan prestasi telah dicapai merentas pelbagai tugasan NLP yang memerlukan inferens.
Kertas kerja ini terutamanya mengkaji kaedah Zero-shot-CoT "untuk menyelesaikan tugasan penaakulan matematik". kepada 78.7%, tetapi masih terdapat dua kelemahan utama:
1 Walaupun rantaian pemikiran yang diikuti oleh model meningkatkan keputusan, ia tidak memeriksa keberkesanan rantaian setiap langkah diikuti;
2. Tiada keyakinan diberikan untuk keputusan ramalan LLM.
MathPrompter
Untuk menangani jurang ini pada tahap tertentu, penyelidik mengambil inspirasi daripada "cara manusia menyelesaikan masalah matematik" dan menguraikan masalah kompleks kepada prosedur pelbagai langkah yang lebih mudah , dan menggunakan pelbagai kaedah untuk mengesahkan kaedah pada setiap langkah.
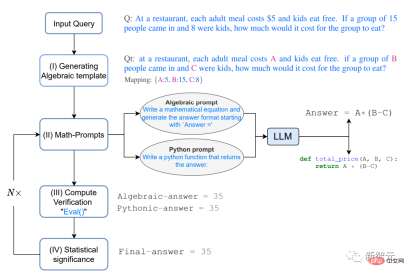
Memandangkan LLM ialah model generatif, ia menjadi sangat sukar untuk memastikan jawapan yang dijana adalah tepat, terutamanya untuk tugasan penaakulan matematik.
Penyelidik memerhati proses pelajar menyelesaikan masalah aritmetik dan merumuskan beberapa langkah yang diambil pelajar untuk mengesahkan penyelesaian mereka:
Pematuhan dengan keputusan yang diketahui Dengan membandingkan penyelesaian dengan keputusan yang diketahui, anda boleh menilai ketepatannya dan membuat pelarasan yang diperlukan apabila masalahnya adalah Ini amat berguna apabila ia berkaitan dengan masalah standard; penyelesaian yang matang.
Pengesahan berbilang membantu mengesahkan keberkesanan penyelesaian dengan mendekati masalah dari pelbagai sudut dan membandingkan hasilnya, memastikan ia munasabah dan tepat.
Semakan silang Proses menyelesaikan masalah adalah seperti yang diperlukan sebagai jawapan akhir yang mengesahkan ketepatan langkah perantaraan dalam proses dapat memberikan pemahaman yang jelas daripada penyelesaian Proses pemikiran di belakangnya.
Pengesahan pengiraanMenggunakan kalkulator atau komputer untuk melakukan pengiraan aritmetik boleh membantu mengesahkan ketepatan jawapan akhir
Khususnya, diberikan soalan S,

Di sebuah restoran, kos setiap hidangan dewasa Harga adalah $5, dan kanak-kanak makan percuma. Jika 15 orang masuk dan 8 daripadanya adalah kanak-kanak, berapakah kos untuk makan bagi golongan ini?
1 Menjana templat Algebra
Selesaikan masalah dahulu bentuk algebra, dengan menggantikan istilah berangka dengan pembolehubah menggunakan pemetaan nilai kunci, kami kemudian mendapat masalah yang diubah suai Qt

2 . Gesaan matematik
Berdasarkan gerak hati yang disediakan oleh proses pemikiran di atas bagi pengesahan berbilang dan semakan silang, dua kaedah berbeza digunakan untuk menjana Qt Analisis penyelesaian, secara algebra dan Pythonic, memberikan LLM petunjuk berikut untuk menjana konteks tambahan untuk Qt.

Gesaan boleh menjadi "Terbitkan ungkapan algebra" atau "Tulis fungsi Python"
Model LLM boleh mengeluarkan ungkapan berikut selepas membalas gesaan.

Pelan analisis yang dijana di atas menyediakan pengguna dengan petua tentang "proses pemikiran pertengahan" LLM Menambah petua tambahan boleh meningkatkan ketepatan keputusan . ketepatan dan ketekalan, yang seterusnya meningkatkan keupayaan MathPrompter untuk menjana penyelesaian yang lebih tepat dan cekap.
3 Pengiraan pengesahan
Gunakan berbilang pembolehubah input dalam kunci rawak Qt A-. peta nilai untuk menilai ungkapan yang dijana dalam langkah sebelumnya, menggunakan kaedah eval() Python untuk menilai ungkapan ini.
Kemudian bandingkan hasil output untuk melihat sama ada konsensus boleh ditemui dalam jawapan, yang juga boleh memberikan tahap keyakinan yang lebih tinggi bahawa jawapan itu betul dan boleh dipercayai.

Setelah ungkapan bersetuju dengan output, gunakan nilai pembolehubah dalam input Q untuk mengira jawapan akhir .
4 Kepentingan statistik
Untuk memastikan konsensus dalam output pelbagai ungkapan, Ulang langkah 2 dan 3 lebih kurang 5 kali dalam eksperimen dan laporkan nilai jawapan yang paling kerap diperhatikan.
Jika tiada konsensus yang jelas, ulangi langkah 2, 3, dan 4.
Hasil eksperimen
Nilai MathPrompter pada set data MultiArith Soalan matematik di dalamnya digunakan secara khusus untuk menguji keupayaan model pembelajaran mesin untuk melaksanakan operasi dan penaakulan aritmetik yang kompleks. . Memerlukan penggunaan pelbagai operasi aritmetik dan penaakulan logik untuk berjaya diselesaikan.
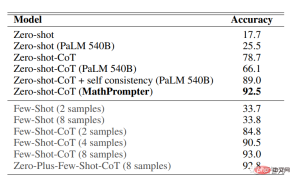
Hasil ketepatan pada dataset MultiArith menunjukkan bahawa MathPrompter berprestasi lebih baik daripada semua Zero-shot dan Zero -shot-CoT garis dasar, meningkatkan ketepatan daripada 78.7% kepada 92.5%
Ia boleh dilihat bahawa prestasi model MathPrompter berdasarkan parameter 175B GPT3 DaVinci adalah setanding dengan model parameter 540B dan Kaedah Few -shot-CoT SOTA yang setara.

Seperti yang dapat dilihat dari jadual di atas, reka bentuk MathPrompter boleh menampung masalah seperti "yang dihasilkan jawapan kadangkala mempunyai perbezaan satu langkah ” masalah boleh dielakkan dengan menjalankan model beberapa kali dan melaporkan hasil konsensus.
Selain itu, masalah bahawa langkah inferens mungkin terlalu panjang boleh diselesaikan dengan kaedah Pythonic atau Algebraic, yang biasanya memerlukan lebih sedikit token
Selain itu, langkah inferens mungkin betul, tetapi hasil pengiraan akhir adalah salah MathPrompter menyelesaikan masalah ini dengan menggunakan fungsi kaedah eval() Python.
Dalam kebanyakan kes, MathPrompter boleh menjana jawapan pertengahan dan akhir yang betul, tetapi terdapat beberapa kes, seperti soalan terakhir dalam jadual, di mana output algebra dan Pythonic adalah konsisten Ya , tetapi terdapat ralat.
Atas ialah kandungan terperinci Ketepatan GPT-3 dalam menyelesaikan masalah matematik telah meningkat kepada 92.5%! Microsoft mencadangkan MathPrompter untuk mencipta model bahasa 'sains' tanpa penalaan halus. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

