Pengenalan terperinci kepada pokok binari JavaScript dan pelbagai algoritma traversal

Artikel ini membawakan anda pengetahuan yang berkaitan tentang javascript terutamanya memperkenalkan butiran pepohon perduaan JavaScript dan pelbagai algoritma traversal memerlukan ia boleh merujuk kepadanya, saya harap ia akan membantu semua orang.

[Cadangan berkaitan: tutorial video javascript, bahagian hadapan web]

Apakah itu binari pokok

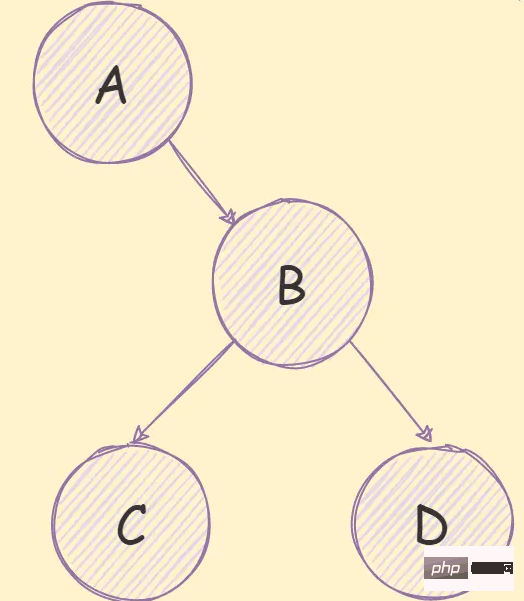
Pokok binari ialah pokok di mana setiap nod hanya boleh mempunyai paling banyak dua nod anak, seperti yang ditunjukkan dalam rajah di bawah:

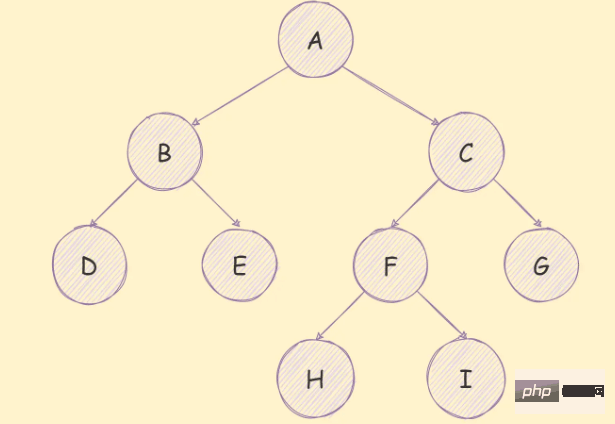
Pokok binari mempunyai ciri-ciri berikut:

• Hanya terdapat i nod pada tahap 2^(i-1) paling banyak
• Jika kedalaman pokok binari ini ialah k, maka Pokok binari mempunyai paling banyak 2^k-1 nod
• Dalam pokok binari yang tidak kosong, jika n0 digunakan untuk mewakili bilangan daun; nod, n2 ialah bilangan nod bukan daun dengan darjah 2, Kemudian kedua-duanya memenuhi hubungan n0 = n2 1.

Pokok binari penuh

Jika dalam pokok binari, kecuali nod daun, darjah setiap nod ialah 2, maka pokok binari ialah pokok binari penuh,

seperti rajah di bawah:

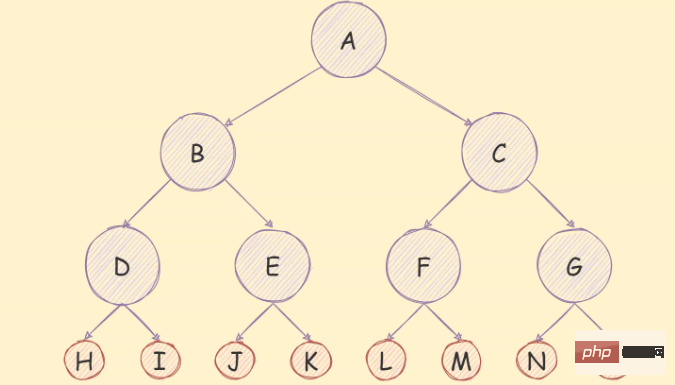
Selain memenuhi ciri pokok binari biasa , pokok binari penuh juga mempunyai ciri berikut: Ciri:

• Tahap npokok binari penuh mempunyai 2^(n-1) nod
• A penuh pokok binari dengan kedalaman k mesti wujud2^k-1 nod, bilangan nod daun ialah 2^(k-1); kedalaman pokok binari penuh dengan
nod ialah
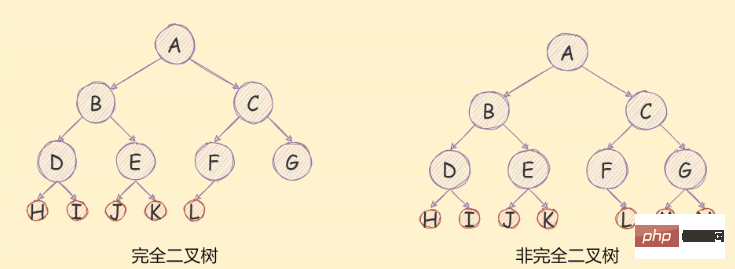
• . nlog_2^(n 1)
Pokok Perduaan Lengkap

Jika pokok perduaan ialah pokok perduaan penuh selepas mengalih keluar lapisan terakhir, dan nod terakhir diedarkan dari kiri ke kanan mengikut urutan

, maka pokok binari ini ialah pokok binari yang lengkap,

seperti yang ditunjukkan di bawah:

Penyimpanan pokok binari

Penyimpanan pokok binari Terdapat dua cara biasa, satu ialah menggunakan

storan tatasusunan

, dan satu lagi ialah menggunakan storan senarai terpaut. Storan tatasusunan

Gunakan tatasusunan untuk menyimpan pokok binari Jika pokok binari yang lengkap ditemui, susunan storan adalah dari atas ke bawah dan dari kiri ke kanan, seperti yang ditunjukkan dalam rajah di bawah:

Jika ia adalah pokok binari yang tidak lengkap, seperti yang ditunjukkan di bawah:

Diperlukan Mula-mula tukarkannya kepada pokok binari yang lengkap dan kemudian simpannya, seperti yang ditunjukkan dalam rajah berikut:

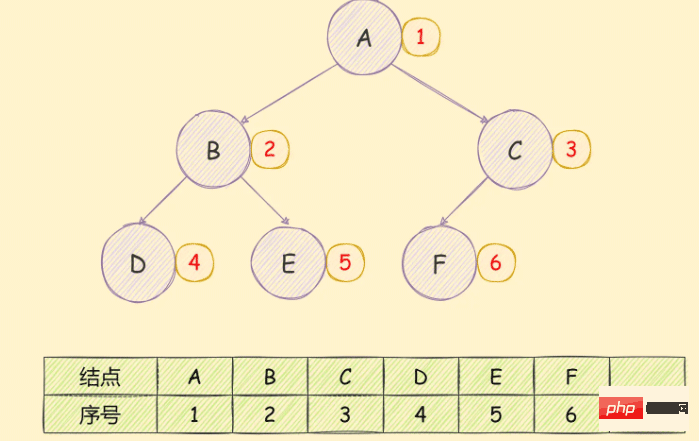
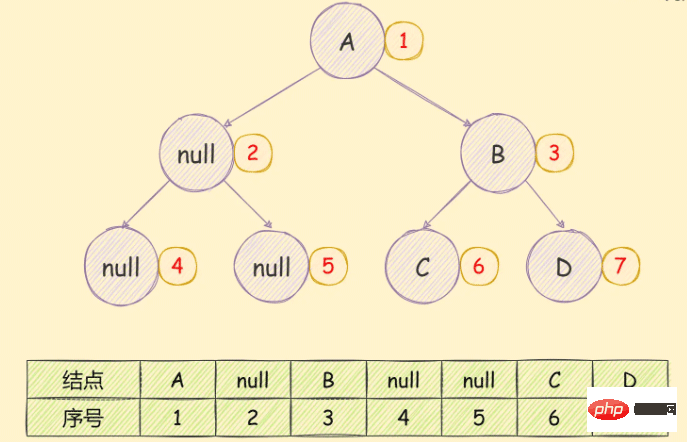Anda boleh jelas melihat pembaziran ruang simpanan.

Storan senarai terpaut

Menggunakan storan senarai terpaut, pokok binari biasanya dibahagikan kepada 3 bahagian, seperti ditunjukkan di bawah:

Ketiga -tiga bahagian ini adalah rujukan kepada subtree kiri, data yang terkandung dalam nod, dan rujukan kepada subtree yang betul.

Algoritma yang berkaitan dengan pokok binari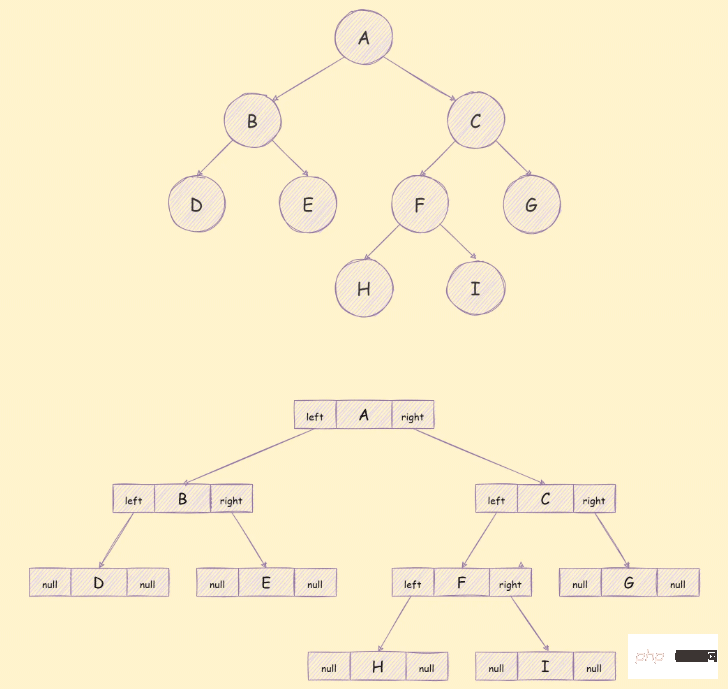

Pokok yang digunakan untuk traversal dalam algoritma berikut adalah seperti berikut

:

Traversal depth-first

// tree.js
const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}
module.exports = bt

Traversal depth-first pada pokok binari adalah konsisten dengan traversal depth-first pada pokok

melawat nod akar; melawati nod akar

• Untuk mengakses nod akar
• left ulangi langkah kedua dan ketiga
• right
Kod pelaksanaan adalah seperti berikut:

Breadth-first traversal

Idea pelaksanaan adalah seperti berikut :

const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}

function dfs(root) {
  if (!root) return
  console.log(root.val)
  root.left && dfs(root.left)
  root.right && dfs(root.right) 
}
dfs(bt)
/** 结果
A B D E C F H I G
*/

Buat baris gilir dan tambahkan nod akar pada baris gilirTurunkan barisan lawan dan aksesnya

Tambah
• dan
di kepala baris gilir ke baris gilir mengikut turutan
• Ulang langkah 2 dan 3 sehingga baris gilir kosong
• leftright
Laksanakan kod Seperti berikut:

Pre-order traversal

Idea pelaksanaan prapesan traversal pokok binari adalah seperti berikut:

function bfs(root) {
  if (!root) return
  const queue = [root]
  while (queue.length) {
    const node = queue.shift()
    console.log(node.val)
    node.left && queue.push(node.left)
    node.right && queue.push(node.right)
  }
}
bfs(bt)
/** 结果
A B C D E F G H I
 */

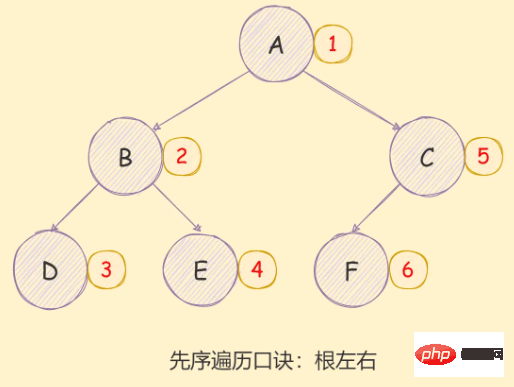
• 访问根节点;
• 对当前节点的左子树进行先序遍历；
• 对当前节点的右子树进行先序遍历；

如下图所示：

递归方式实现如下：

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

迭代方式实现如下：

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

中序遍历

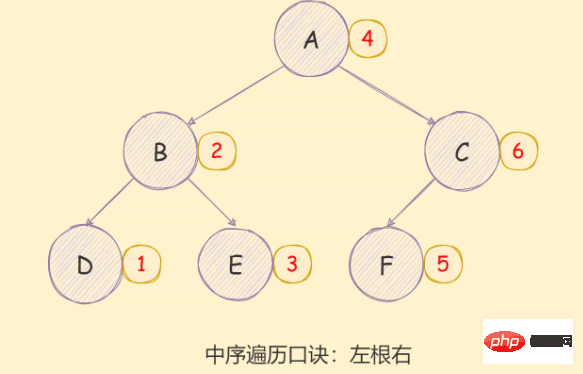
二叉树的中序遍历实现思想如下：

• 对当前节点的左子树进行中序遍历；
• 访问根节点;
• 对当前节点的右子树进行中序遍历；

如下图所示：

递归方式实现如下：

const bt = require('./tree')

// 递归版
function inorder(root) {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}
inorder(bt)

/** 结果
D B E A H F I C G
*/

迭代方式实现如下：

// 非递归版
function inorder(root) {
  if (!root) return
  const stack = []
  // 定义一个指针
  let p = root
  // 如果栈中有数据或者p不是null，则继续遍历
  while (stack.length || p) {
    // 如果p存在则一致将p入栈并移动指针
    while (p) {
      // 将 p 入栈，并以移动指针
      stack.push(p)
      p = p.left
    }

    const node = stack.pop()
    console.log(node.val)
    p = node.right
  }
}
inorder(bt)
/** 结果
D B E A H F I C G
*/

后序遍历

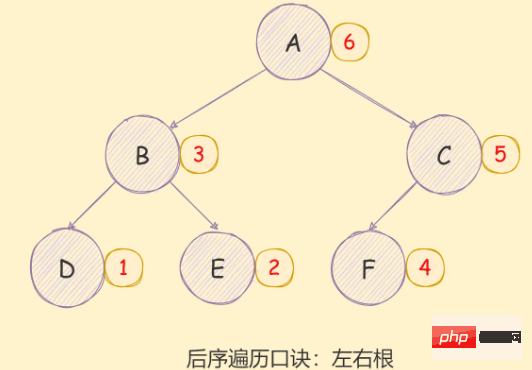
二叉树的后序遍历实现思想如下：

• 对当前节点的左子树进行后序遍历；
• 对当前节点的右子树进行后序遍历；
• 访问根节点;

如下图所示：

递归方式实现如下：

const bt = require('./tree')

// 递归版
function postorder(root) {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

迭代方式实现如下：

// 非递归版
function postorder(root) {
  if (!root) return
  const outputStack = []
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    outputStack.push(node)
    // 这里先入left需要保证left后出，在stack中后出，就是在outputStack栈中先出
    node.left && stack.push(node.left)
    node.right && stack.push(node.right)
  }
  while (outputStack.length) {
    const node = outputStack.pop()
    console.log(node.val)
  }
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

【相关推荐：javascript视频教程、web前端】

Atas ialah kandungan terperinci Pengenalan terperinci kepada pokok binari JavaScript dan pelbagai algoritma traversal. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!