Latihan aksiomatik membolehkan LLM mempelajari penaakulan kausal: model 67 juta parameter adalah setanding dengan trilion tahap parameter GPT-4

Tunjukkan rantai sebab kepada LLM dan ia akan mempelajari aksiom.

AI sudah pun membantu ahli matematik dan saintis membuat penyelidikan Contohnya, ahli matematik terkenal Tao Zhexuan telah berulang kali berkongsi pengalaman penyelidikan dan penerokaannya dengan bantuan GPT dan alatan AI yang lain. Untuk AI bersaing dalam bidang ini, keupayaan penaakulan sebab yang kukuh dan boleh dipercayai adalah penting.

Penyelidikan yang akan diperkenalkan dalam artikel ini mendapati bahawa model Transformer yang dilatih mengenai demonstrasi aksiom transitiviti sebab bagi graf kecil boleh digeneralisasikan kepada aksiom transitiviti untuk graf besar.

Dalam erti kata lain, jika Transformer belajar melakukan penaakulan sebab yang mudah, ia mungkin digunakan untuk penaakulan sebab yang lebih kompleks. Rangka kerja latihan aksiom yang dicadangkan oleh pasukan adalah paradigma baharu untuk mempelajari penaakulan sebab berdasarkan data pasif, yang boleh digunakan untuk mempelajari aksiom sewenang-wenang selagi demonstrasi mencukupi.

Pengenalan

Penaakulan sebab boleh ditakrifkan sebagai satu set proses penaakulan yang mematuhi aksiom atau peraturan yang telah ditetapkan khusus untuk sebab-akibat. Sebagai contoh, peraturan pemisahan-d (pemisahan terarah) dan do-kalkulus boleh dianggap sebagai aksiom, manakala spesifikasi set collider atau set pintu belakang boleh dianggap sebagai peraturan yang diperoleh daripada aksiom.

Secara amnya, inferens sebab menggunakan data yang sepadan dengan pembolehubah dalam sistem. Aksiom atau peraturan boleh disepadukan ke dalam model pembelajaran mesin dalam bentuk bias induktif melalui regularisasi, seni bina model atau pemilihan pembolehubah tertentu.

Berdasarkan perbezaan jenis data yang tersedia (data pemerhatian, data intervensi, data balas fakta), "tangga sebab" yang dicadangkan oleh Judea Pearl mentakrifkan kemungkinan jenis inferens sebab.

Memandangkan aksiom ialah asas sebab musabab, kita pasti tertanya-tanya sama ada kita boleh terus menggunakan model pembelajaran mesin untuk mempelajari aksiom. Iaitu, bagaimana jika cara untuk mempelajari aksiom bukanlah untuk mempelajari data yang diperoleh melalui beberapa proses penjanaan data, tetapi secara langsung untuk mempelajari demonstrasi simbolik aksiom (dan dengan itu mempelajari penaakulan sebab-akibat)?

Berbanding dengan model kausal khusus tugas yang dibina menggunakan pengedaran data khusus, model sedemikian mempunyai kelebihan: ia boleh mencapai penaakulan sebab dalam pelbagai senario hiliran yang berbeza. Soalan ini menjadi penting apabila model bahasa memperoleh keupayaan untuk mempelajari data simbolik yang dinyatakan dalam bahasa semula jadi.

Malah, beberapa penyelidikan baru-baru ini telah menilai sama ada model bahasa besar (LLM) mampu melakukan inferens sebab dengan mencipta penanda aras yang mengekodkan masalah inferens sebab dalam bahasa semula jadi.

Pasukan penyelidik dari Microsoft, MIT, dan Institut Teknologi India Hyderabad (IIT Hyderabad) juga telah mengambil langkah penting ke arah ini: mencadangkan kaedah untuk mempelajari inferens sebab melalui latihan aksiomatik .

• Tajuk kertas: Mengajar Penaakulan Penyebab Transformers melalui Latihan Axiomatic
• Alamat kertas: https://arxiv.org/pdf/2407.07612

Latihan Axiomatic

Mereka menganggap, Aksiom sebab boleh dinyatakan sebagai tuple simbolik berikut 〈premis, hipotesis, hasil〉. Antaranya, hipotesis merujuk kepada hipotesis, iaitu, pernyataan sebab akibat ialah premis, yang merujuk kepada sebarang maklumat yang relevan yang digunakan untuk menentukan sama ada pernyataan itu adalah "benar" secara semula jadi; Hasilnya boleh menjadi "ya" atau "tidak" mudah.

Contohnya, aksiom kolider daripada kertas "Bolehkah model bahasa besar membuat kesimpulan sebab daripada korelasi?", dan kesimpulannya ialah "ya".

Berdasarkan templat ini, sejumlah besar tupel sintetik boleh dihasilkan dengan mengubah suai nama pembolehubah, nombor pembolehubah, susunan pembolehubah, dll.

Untuk menggunakan Transformer untuk mempelajari aksiom sebab dan melaksanakan latihan aksiom, pasukan menggunakan kaedah berikut untuk membina set data, fungsi kehilangan dan pembenaman kedudukan.

Latihan aksiomatik: Set data, fungsi kehilangan dan kompilasi kedudukan

Data latihan

berdasarkan label "hypopresis" tertentu yang sesuai ( Ya atau tidak). Untuk mencipta set data latihan, pasukan menyenaraikan semua tupel yang mungkin {(P, H, L)}_N di bawah tetapan pembolehubah tertentu X, Y, Z, A, dengan P ialah premis dan H ialah hipotesis, L ialah label (Ya atau tidak).

Diberi premis P berdasarkan beberapa rajah sebab, jika hipotesis P boleh diterbitkan dengan menggunakan aksiom tertentu (satu kali atau lebih), maka label L ialah Ya, jika tidak, ia adalah Tidak.

Sebagai contoh, andaikan bahawa graf sebab sebenar yang mendasari sistem mempunyai topologi rantai: X_1 → X_2 → X_3 →・・・→ X_n. Kemudian, premis yang mungkin ialah X_1 → X_2 ∧ X_2 → X_3, kemudian andaikan X_1 → Aksiom di atas boleh digunakan secara induktif berkali-kali untuk menghasilkan tupel latihan yang lebih kompleks.

Untuk tetapan latihan, bina set data sintetik D menggunakan tika N aksiom yang dijana oleh aksiom transitiviti. Setiap kejadian dalam D dibina daripada bentuk (P_i, H_ij, L_ij),
, dengan n ialah bilangan nod dalam setiap premis ke-i. P ialah premis, iaitu ungkapan bahasa semula jadi bagi struktur penyebab tertentu (seperti X menyebabkan Y, Y menyebabkan Z diikuti dengan soalan H (seperti X menyebabkan Y?); atau tidak). Borang ini secara berkesan meliputi semua pasangan nod untuk setiap rantai unik dalam graf penyebab yang diberikan.

Fungsi kehilangan

Memandangkan set data, fungsi kehilangan ditakrifkan berdasarkan label kebenaran tanah bagi setiap tuple, dinyatakan sebagai:
Analisis menunjukkan bahawa berbanding ramalan token seterusnya, menggunakan Kerugian ini boleh membuahkan hasil yang memberangsangkan.

Pengekodan kedudukan

Selain fungsi latihan dan kehilangan, pilihan pengekodan kedudukan juga merupakan satu lagi faktor penting. Pengekodan kedudukan boleh memberikan maklumat penting tentang kedudukan mutlak dan relatif token dalam urutan.

Kertas terkenal "Perhatian adalah semua yang anda perlukan" mencadangkan strategi pengekodan kedudukan mutlak yang menggunakan fungsi berkala (fungsi sinus atau kosinus) untuk memulakan kod ini.

🎜🎜🎜Pengekodan kedudukan mutlak boleh memberikan nilai tertentu untuk semua kedudukan bagi sebarang panjang jujukan. Walau bagaimanapun, beberapa kajian menunjukkan bahawa pengekodan kedudukan mutlak sukar untuk mengatasi tugas generalisasi panjang Transformer. Dalam varian APE yang boleh dipelajari, setiap pembenaman kedudukan dimulakan secara rawak dan dilatih menggunakan model. Kaedah ini bergelut dengan urutan yang lebih panjang daripada semasa latihan, kerana benam kedudukan baharu masih tidak terlatih dan tidak dimulakan. 🎜🎜🎜🎜🎜Menariknya, penemuan baru-baru ini telah menunjukkan bahawa mengalih keluar benam kedudukan dalam model autoregresif boleh meningkatkan keupayaan generalisasi panjang model, dan mekanisme perhatian semasa penyahkodan autoregresif adalah mencukupi untuk mengekod maklumat kedudukan. Pasukan ini menggunakan pengekodan kedudukan yang berbeza untuk memahami impaknya terhadap generalisasi dalam tugas sebab, termasuk pengekodan kedudukan boleh dipelajari (LPE), pengekodan kedudukan sinusoidal (SPE) dan tiada pengekodan kedudukan (NoPE).

Untuk meningkatkan keupayaan generalisasi model, pasukan juga menggunakan gangguan data, termasuk gangguan panjang, nama nod, susunan rantai dan status cawangan.

Eksperimen

Soalan berikut timbul: Jika model dilatih menggunakan data ini, bolehkah model belajar menggunakan aksiom ini kepada senario baharu?

Untuk menjawab soalan ini, pasukan melatih model Transformer dari awal menggunakan demonstrasi simbolik aksiom bebas sebab akibat ini.

Untuk menilai prestasi generalisasi, mereka berlatih pada rantai aksiom bebas sebab bersaiz 3-6 nod yang mudah, dan kemudian menguji beberapa aspek prestasi generalisasi yang berbeza, termasuk prestasi generalisasi panjang (rantaian saiz 7-15), generalisasi nama (nama pembolehubah yang lebih panjang), generalisasi berjujukan (rantaian dengan tepi terbalik atau nod dikocok), generalisasi struktur (graf dengan cabang) ). Rajah 1 menggambarkan cara menilai generalisasi struktur Transformer.

Secara khusus, mereka melatih model berasaskan penyahkod dengan 67 juta parameter berdasarkan seni bina GPT-2. Model ini mempunyai 12 lapisan perhatian, 8 kepala perhatian dan 512 dimensi benam. Mereka melatih model dari awal pada setiap set data latihan. Untuk memahami kesan pembenaman kedudukan, mereka juga mengkaji tiga tetapan pembenaman kedudukan: pengekodan kedudukan sinusoidal (SPE), pengekodan kedudukan boleh dipelajari (LPE) dan tiada pengekodan kedudukan (NoPE).

Keputusan ditunjukkan dalam Jadual 1, Rajah 3 dan Rajah 4.

Jadual 1 memberikan ketepatan model yang berbeza apabila dinilai pada rantai sebab yang lebih besar yang tidak dilihat semasa latihan. Dapat dilihat bahawa prestasi model baharu TS2 (NoPE) adalah setanding dengan skala trilion parameter GPT-4.

Rajah 3 ialah hasil penilaian kebolehan generalisasi pada jujukan kausal dengan nama nod yang lebih panjang (lebih panjang daripada set latihan) dan kesan daripada pembenaman kedudukan yang berbeza.

Rajah 4 menilai keupayaan generalisasi pada jujukan sebab-sebab ghaib yang lebih lama.

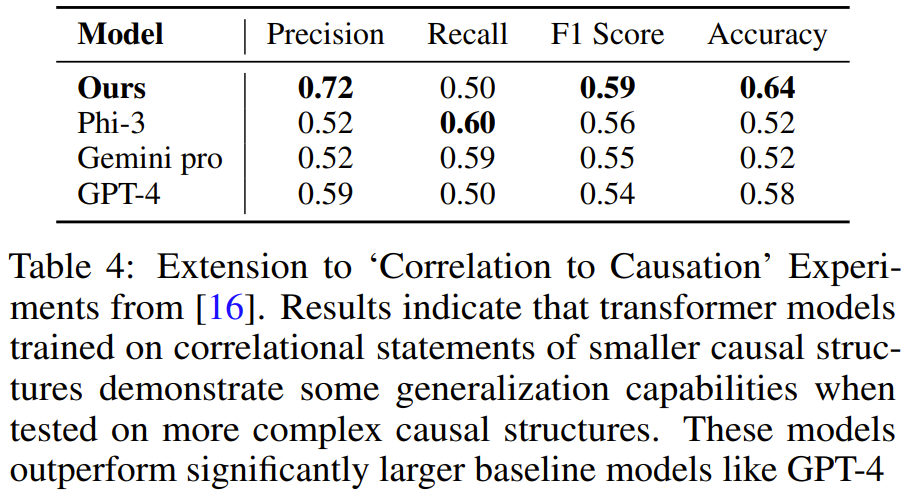
Mereka mendapati bahawa model yang dilatih pada rantai mudah boleh menggeneralisasikan kepada berbilang aplikasi aksiom pada rantai yang lebih besar, tetapi tidak boleh membuat generalisasi kepada senario yang lebih kompleks seperti generalisasi berjujukan atau struktur. Walau bagaimanapun, jika model dilatih pada set data bercampur yang terdiri daripada rantaian ringkas serta rantaian dengan tepi terbalik rawak, model itu digeneralisasikan dengan baik kepada pelbagai senario penilaian.

Melanjutkan keputusan mengenai generalisasi panjang pada tugasan NLP, mereka mendapati kepentingan pembenaman kedudukan dalam memastikan generalisasi sebab merentasi panjang dan dimensi lain. Model berprestasi terbaik mereka tidak mempunyai pengekodan kedudukan, tetapi mereka juga mendapati bahawa pengekodan sinusoidal berfungsi dengan baik dalam beberapa kes.

Kaedah latihan aksiom ini juga boleh digeneralisasikan kepada masalah yang lebih sukar, seperti yang ditunjukkan dalam Rajah 5. Iaitu, berdasarkan premis yang mengandungi pernyataan kebebasan statistik, matlamat tugas adalah untuk membezakan korelasi daripada sebab. Menyelesaikan tugas ini memerlukan pengetahuan tentang beberapa aksiom, termasuk pemisahan-d dan sifat Markov.

Pasukan menghasilkan data latihan sintetik menggunakan kaedah yang sama seperti di atas, dan kemudian melatih model Didapati Transformer yang dilatih pada demonstrasi tugasan yang mengandungi 3-4 pembolehubah boleh belajar menyelesaikan masalah yang mengandungi 5 pembolehubah tugasan. Dan pada tugas ini, model itu lebih tepat daripada LLM yang lebih besar seperti GPT-4 dan Gemini Pro.

Pasukan itu berkata: "Penyelidikan kami menyediakan paradigma baharu untuk model pengajaran untuk mempelajari penaakulan sebab melalui demonstrasi simbolik aksiom, yang kami panggil latihan aksiomatik dan latihan kaedah ini Prosedurnya adalah umum: selagi sebagai aksiom boleh dinyatakan dalam format tupel simbolik, ia boleh dipelajari menggunakan kaedah ini.

Atas ialah kandungan terperinci Latihan aksiomatik membolehkan LLM mempelajari penaakulan kausal: model 67 juta parameter adalah setanding dengan trilion tahap parameter GPT-4. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!