행렬 곱셈의 실행 과정을 3차원으로 표시할 수 있다면 그때는 행렬 곱셈을 배우는 것이 그리 어렵지 않을 것입니다.
현재 행렬 곱셈은 기계 학습 모델의 구성 요소이자 다양한 강력한 AI 기술의 기초가 되었습니다. 실행 방법을 이해하면 이 AI와 점점 지능화되는 세계를 더 깊이 이해하는 데 확실히 도움이 됩니다.
PyTorch 블로그의 이 기사에서는 행렬 곱셈과 행렬 곱셈 조합을 위한 시각화 도구인 mm을 소개합니다.
MM은 일반적인 2차원 차트에 비해 3가지 공간 차원을 모두 사용하기 때문에 아이디어를 직관적으로 표시하고 자극하는 데 도움이 되며, 인지적 오버헤드를 덜 사용합니다. 특히 시각적 및 공간적 능력이 뛰어난 사람들에게는 (그러나 이에 국한되지 않음) 생각.
그리고 훈련된 가중치를 로드하는 기능과 함께 행렬 곱셈을 결합하는 3차원을 통해 mm는 큰 복합 표현식(예: 주의 머리)을 시각화하고 실제 행동 패턴을 관찰할 수 있습니다.
mm은 완전 대화형이며 브라우저 또는 노트북 iframe에서 실행되며 전체 상태를 URL에 저장하므로 링크는 공유 가능한 세션입니다(이 문서의 스크린샷과 비디오에는 링크가 있습니다. 해당 시각화 열기 이 도구에 대한 자세한 내용은 원본 블로그를 참조하세요. 이 참조 가이드에서는 사용 가능한 모든 기능을 설명합니다.
도구 주소: https://bhosmer.github.io/mm/ref.html
원래 블로그 텍스트: https://pytorch.org/blog/inside-the-matrix
This 기사는 첫 번째로 시각화 방법을 소개하고, 간단한 행렬 곱셈과 표현식을 시각화하여 직관을 구축한 다음 몇 가지 확장된 예를 살펴보겠습니다.
소개: 이 시각화가 더 나은 이유는 무엇입니까?
준비: 애니메이션 - 정규 행렬 곱셈 분해가 어떻게 작동하는지 확인하세요.
준비: 표현식 - 몇 가지 기본 표현식 구성 요소를 빠르게 살펴보세요.
주의 머리에 대해 자세히 살펴보기: NanoGPT를 사용한 심층 살펴보기 GPT-2에 대한 한 쌍의 어텐션 헤드의 구조, 값 및 계산 동작
주의 병렬화: 최근 Blockwise Parallel Transformer 논문의 예를 사용하여 어텐션 헤드의 병렬화를 시각화합니다.
attention 레이어의 크기: 전체 attention 레이어를 단일 구조로 시각화할 때 attention 레이어의 MHA 절반과 FFA 절반은 함께 어떻게 보일까요? 자동 회귀 디코딩 프로세스 중에 이미지가 어떻게 변경됩니까?
LoRA: 이 어텐션 헤드 아키텍처에 대한 자세한 시각적 설명
1 소개
mm의 시각화 접근 방식은 행렬 곱셈이 본질적으로 3차원 연산이라는 전제를 기반으로 합니다.
즉,

은 실제로 다음과 같이 그릴 수 있습니다.

이러한 방식으로 큐브에 행렬 곱셈을 래핑하면 매개변수 모양, 결과 모양 및 공유 차원 사이의 올바른 관계 모두 제자리에 있습니다.
이제 행렬 곱셈 계산은 기하학적 의미가 있습니다. 결과 행렬의 각 위치 i,j는 L의 i번째 행에서 확장되는 큐브 내부의 깊이 차원 k를 따라 실행되는 벡터를 고정합니다. 수평면은 수직선과 교차합니다 R의 j번째 열에서 연장되는 평면. 이 벡터를 따라 왼쪽 인수와 오른쪽 인수의 (i, k) (k, j) 요소 쌍이 만나 곱해지고 결과 곱은 k를 따라 합산되어 결과의 i, j 위치에 배치됩니다.
행렬 곱셈의 직관적인 의미는 다음과 같습니다.
1. 두 개의 직교 행렬을 큐브 내부에 투영합니다.
2 각 교차점에서 한 쌍의 값을 곱하여 곱 그리드를 얻습니다. 세 번째 직교 차원을 따라 합산하여 결과 행렬을 생성합니다.
방향의 경우 도구는 큐브 내부에 결과 행렬을 가리키는 화살표를 표시합니다. 왼쪽 매개변수에서는 파란색 플레칭이, 오른쪽 매개변수에서는 빨간색 플레치가 표시됩니다. 이 도구는 또한 각 행렬의 행 축을 나타내는 흰색 표시기 선을 표시합니다. 단, 이 스크린샷에서는 이러한 선이 흐릿하게 표시되어 있습니다.
레이아웃 제약 조건은 간단하고 간단합니다.
- 왼쪽 매개변수와 결과는 공유 높이(i) 차원을 따라 인접해야 합니다.
- 오른쪽 매개변수와 결과는 공유 너비를 따라 인접해야 합니다. (j) 차원
- 왼쪽 및 오른쪽 매개변수는 공유된(왼쪽 너비/오른쪽 높이) 차원을 따라 인접해야 하며 이는 행렬 곱셈의 깊이(k) 차원이 됩니다.
- 이 기하학적 표현을 사용할 수 있습니다. 표준 행렬 곱셈 인수분해는 다음에 살펴보겠지만 복잡한 행렬 곱셈의 중요하지 않은 조합을 탐색하기 위한 견고한 기초와 직관적인 기초를 제공합니다.
더 복잡한 예제를 살펴보기 전에 도구에 대한 직관적인 이해를 돕기 위해 이 시각화 스타일이 어떤 모습인지 살펴보겠습니다.
2a 도트곱먼저 기존 알고리즘을 살펴보겠습니다. 해당 왼쪽 행과 오른쪽 열의 내적을 계산하여 각 결과 요소를 계산합니다. 여기 애니메이션에서 볼 수 있듯이 곱해진 값 벡터는 큐브 내부를 휩쓸며 매번 해당 위치에 합산된 결과를 제공합니다. 여기서 L에는 1(파란색) 또는 -1(빨간색)로 채워진 행 블록이 있고, R에는 비슷하게 채워진 열 블록이 있습니다. 여기서 k는 24이므로 결과 행렬(L@R)의 파란색 값은 24이고 빨간색 값은 -24입니다. 2b 행렬-벡터 곱 행렬-벡터 곱으로 분해됨 행렬 곱셈은 내부를 가로질러 수평으로 스윕하므로 수직면(왼쪽 매개변수와 오른쪽 매개변수의 각 열의 곱)처럼 보입니다. 큐브, 결과에 열을 플롯합니다. 예제가 간단하더라도 분해의 중간 값을 관찰하는 것은 흥미로울 수 있습니다. 예를 들어, 가운데에 있는 행렬-벡터 곱은 무작위로 초기화된 매개변수를 사용할 때 수직 패턴을 강조한다는 점에 유의하세요. 이는 각 중간 값이 왼쪽에 있는 매개변수의 열 크기 복사본이라는 사실을 반영합니다. 2c 벡터 - 행렬 곱 이 벡터로 분해됨 - 행렬 곱의 행렬 곱셈은 큐브 내부를 따라 내려갈 때 결과에 행을 그리는 수평면처럼 보입니다. 전환 무작위로 초기화된 매개변수를 사용하면 행렬-벡터 곱과 유사한 패턴을 볼 수 있습니다. 이번에는 수평 모드에서만 볼 수 있습니다. 이는 각 중간 벡터 행렬 곱이 오른쪽 매개변수의 행 크기 조정된 복사본이라는 사실에 해당합니다. 행렬 곱셈이 매개변수의 순위합 구조를 어떻게 나타내는지 생각할 때 유용한 접근법은 계산에서 동시에 발생하는 두 가지 모드를 상상하는 것입니다. 2d 외부 곱의 합산 세 번째 평면 분해는 k축을 따라, 행렬 곱셈 결과는 벡터 외부 곱을 점별로 합산하여 계산됩니다. 여기서는 외부 곱 평면이 큐브를 "뒤에서 앞으로" 스윕하여 결과에 누적되는 것을 볼 수 있습니다. 이 분해를 위해 무작위로 초기화된 행렬을 사용하면 값뿐만 아니라 결과도 볼 수 있습니다. 의 순위는 1순위의 각 외부 제품이 추가될 때마다 누적됩니다. 이것은 또한 근사화되는 행렬이 낮은 행렬일 때 "낮은 순위 인수분해"(즉, 깊이 차원에서 더 작은 매개변수를 사용하여 행렬 곱셈을 구성하여 행렬을 근사화하는 것)가 가장 잘 작동하는 이유를 직관적으로 설명합니다. 나중에 언급할 LoRA입니다. 3 워밍업: 표현식 어떤 방법으로 이 시각화 방법을 행렬 곱셈의 분해로 확장할 수 있나요? 이전 예에서는 행렬 L 및 R의 단일 행렬 곱셈 L @ R을 시각화했지만, L 및/또는 R 자체가 행렬 곱셈이라면 어떻게 될까요? 이 접근 방식은 복합 표현에 적합하다는 것이 밝혀졌습니다. 핵심 규칙은 간단합니다. 하위 표현식 (하위)행렬 곱셈은 상위 행렬 곱셈과 동일한 레이아웃 제약을 받는 또 다른 큐브입니다. 하위 행렬 곱셈의 결과 면은 공유 결합과 마찬가지로 상위 행렬 곱셈의 매개변수 면이기도 합니다. 공유 전자. 이러한 제약 내에서 필요에 따라 부분행렬 곱셈의 다양한 측면을 배열할 수 있습니다. 여기서는 교대로 볼록한 큐브와 오목한 큐브를 생성하는 도구의 기본 구성표가 사용됩니다. 이 레이아웃은 실제로 잘 작동하여 폐색을 최소화하면서 공간을 최대화합니다. (그러나 레이아웃은 완전히 사용자 정의 가능합니다. 자세한 내용은 mm 도구 페이지를 참조하십시오.) 이 섹션에서는 독자가 이 시각적 표현에 익숙해지고 그로부터 새로운 직관을 얻을 수 있도록 기계 학습 모델의 일부 주요 구성 요소를 시각화합니다. 3a 왼쪽 연관 표현 (A @ B) @ C 형식의 두 가지 표현이 아래에 소개되며 각각 고유한 모양과 특성을 갖습니다. (참고: mm는 행렬 곱셈이 왼쪽 연관이라는 규칙을 따르므로 (A @ B) @ C는 간단히 A @ B @ C로 쓸 수 있습니다.) 먼저 A @ B @ C에 매우 독특한 FFN 모양을 지정합니다. "숨겨진 차원"은 "입력" 또는 "출력" 차원보다 넓습니다. (구체적으로 이 예에서는 B의 너비가 A 또는 C의 너비보다 크다는 의미입니다.) 단일 행렬 곱셈 예와 마찬가지로 부동 화살표는 결과 행렬을 가리키며, 파란색 플레칭은 왼쪽 인수의 경우 빨간색 플레칭은 오른쪽 매개변수에서 비롯됩니다. 그리고 B의 너비가 A 또는 C의 너비보다 작을 경우 오토인코더의 모양과 유사하게 A @ B @ C의 시각화에 병목 현상이 발생합니다. 교대 범프 모듈의 패턴은 임의 길이의 체인으로 확장될 수도 있습니다. 예를 들어 다음 다층 병목 현상은 다음과 같습니다. 3b 오른쪽 연관 표현 다음으로 오른쪽 연관 표현 A를 시각화합니다. @(B@C). 왼쪽 연관 표현식의 수평 확장과 유사합니다. 루트 표현식의 왼쪽 매개변수에서 시작한다고 할 수 있으며, 오른쪽 연관 표현식 체인은 루트 표현식의 오른쪽 매개변수에서 시작하여 수직으로 확장됩니다. 때때로 오른쪽 조합 형태로 형성된 MLP를 볼 수 있습니다. 여기서 오른쪽은 열 형식 입력이고 가중치 레이어는 오른쪽에서 왼쪽으로 이어집니다. 위에 묘사된 2계층 FFN 예제의 행렬을 사용하면(적절한 전치 후) 다음과 같습니다. 이제 C는 입력이고, B는 첫 번째 계층이고, A는 두 번째 계층입니다. 또한, 플레칭 색상(왼쪽은 파란색, 오른쪽은 빨간색)을 제외하고 왼쪽과 오른쪽 매개변수를 구별하는 두 번째 시각적 신호는 방향입니다. 왼쪽의 매개변수 행은 결과 행과 동일 평면에 있습니다. 동일한 축 (i) 스택. 위의 (B @ C) 예를 들어, 두 힌트 모두 B가 왼쪽 매개변수임을 알려줄 수 있습니다. 3c 이진 표현식 시각화 도구가 유용하려면 간단한 교육 예제에 사용될 뿐만 아니라 더 복잡한 표현식에도 쉽게 사용할 수 있어야 합니다. 실제 사용 사례에서 주요 구조적 구성 요소는 이진 표현식, 즉 왼쪽과 오른쪽에 하위 표현식이 있는 행렬 곱셈입니다. 여기에는 (A @ B) @ (C @ D) 모양의 가장 간단한 표현이 시각화되어 있습니다. 3d 참고 사항: 분할 및 병렬 처리 이 주제에 대한 완전한 설명은 이 이상입니다. 이 기사의 범위이지만 나중에 주목 헤드 섹션에서 실제적인 유용성을 살펴보겠습니다. 하지만 준비를 위해 간단한 기하학적 분할을 통해 이러한 시각화 스타일이 병렬화된 복합 표현식에 대한 추론을 어떻게 매우 직관적으로 만들 수 있는지 두 가지 간단한 예를 살펴보세요. 첫 번째 예는 위의 왼쪽 조인 다중 계층 병목 현상 예에 일반적인 "데이터 병렬" 분할을 적용하는 것입니다. i를 따라 분할하여 초기 왼쪽 매개변수("배치")와 모든 중간 결과("활성화")를 분할하지만 후속 매개변수("가중치")는 분할하지 않습니다. 이 기하학은 다음과 같은 표현을 만듭니다. 액터는 분할되어 그대로 유지됩니다. 두 번째 예는 명확한 기하학적 지원 없이는 직관적으로 이해하기 어렵습니다. 표현식을 분할하고 오른쪽 자식을 분할하여 이진 표현식을 병렬화하여 왼쪽 하위 표현식을 표현하는 방법을 보여줍니다. i축을 따라 표현식을 나누고 k축을 따라 부모 표현식을 분할합니다. 4 주의 머리 속으로 깊이 들어가기 이제 GPT-2의 주목 헤드를 살펴보겠습니다. 특히 NanoGPT의 5번째 레이어 중 4번째 헤드의 "gpt2"(소형) 구성(레이어 수 = 12, 헤드 수 = 12, 임베딩 수) = 768), HuggingFace를 통해 OpenAI의 가중치를 사용합니다. 입력 활성화는 256개의 토큰이 포함된 OpenWebText 교육 샘플의 정방향 전달에서 가져옵니다. 이 특정 머리에는 특별한 것이 없습니다. 주로 매우 일반적인 주의 패턴을 계산하고 활성화가 구조화되어 흥미로운 질감을 보여주는 모델 중간에 위치하기 때문에 선택되었습니다. 4a 구조 이 완전한 주의 머리는 입력에서 시작하여 예상 출력으로 끝나는 단일 복합 표현으로 시각화됩니다. (참고: 자급자족을 보장하기 위해 Megatron-LM에 대해 여기에 설명된 대로 각 헤드에 대해 출력 투영이 수행됩니다.) 이 계산에는 6개의 행렬 곱셈이 포함됩니다. 여기에서 수행되는 작업에 대한 간략한 설명: 풍차의 블레이드는 행렬 곱셈 1, 2, 3 및 6입니다. 전자 세트는 Q, K 및 V에 대한 입력의 내부 투영이고, 후자는 attn @ V에서 다시 임베딩으로의 외부 투영입니다. 치수. 중앙에는 두 개의 행렬 곱셈이 있습니다. 첫 번째는 주의 점수(뒷면의 볼록 큐브)를 계산한 다음 이를 사용하여 값 벡터를 기반으로 출력 토큰(앞의 오목 큐브)을 얻습니다. 인과성은 주의 점수가 아래쪽 삼각형을 형성한다는 것을 의미합니다. 하지만 이 도구를 더 자세히 이해하기 위해서는 이 도구의 구조와 흐르는 실제 값을 더 자세히 이해하기 위해 단지 스크린샷이나 아래 동영상을 보는 것보다 독자가 직접 자세히 살펴보는 것이 더 나을 것입니다. 계산 과정. 4b 합계 값 계산 여기 어텐션 헤드의 계산 과정에 대한 애니메이션이 있습니다. 구체적으로, 우리는 (예: K_t와 V가 미리 계산된 위의 행렬 곱셈 1, 4, 5 및 6)이 벡터 행렬 곱의 융합된 체인으로 계산되는 것을 보고 있습니다. 각 항목은 다음을 통과합니다. 입력부터 출력까지 한 단계로 집중합니다. 이 애니메이션에 대한 더 많은 옵션은 나중에 병렬화 섹션에서 다루겠지만 먼저 계산된 값이 무엇을 알려주는지 살펴보겠습니다. 흥미로운 내용을 많이 볼 수 있습니다. 주의 계산을 논의하기 전에 하위 Q와 K_t의 모양이 얼마나 놀라운지 알 수 있습니다. Q @ K_t 벡터 매트릭스 제품 애니메이션을 확대하면 훨씬 더 생생해 보입니다. Q와 K의 많은 수의 채널(내장 위치)이 시퀀스에서 어느 정도 일정한 것처럼 보입니다. 이는 유용한 주의 신호를 의미합니다. 소수의 내장 드라이버 세트에 의해서만 생성될 수 있습니다. 이 현상을 이해하고 활용하는 것은 SysML ATOM 변환기 효율성 프로젝트의 일부입니다. 아마도 사람들에게 가장 친숙한 것은 주의 매트릭스에 나타나는 강력하지만 불완전한 대각선일 것입니다. 이는 이 모델(그리고 많은 트랜스포머)의 많은 관심 헤드에 나타나는 일반적인 패턴입니다. 이는 지역적 관심을 불러일으킬 수 있습니다. 출력 토큰 위치 바로 앞의 작은 동네에 있는 가치 토큰은 출력 토큰의 콘텐츠 패턴을 크게 결정합니다. 그러나 이 동네의 크기와 그 안에 있는 개별 토큰의 영향력은 크게 다릅니다. 이는 어텐션 그리드의 대각선을 벗어난 서리에서 볼 수 있으며 또한 attn [i 시퀀스를 따라 하강하는 어텐션 매트릭스에서도 볼 수 있습니다. ] @ V 벡터 - 매트릭스 제품 평면에 보이는 파동 패턴입니다. 그러나 지역 이웃만이 주목할 가치가 있는 것은 아닙니다. 주의 그리드의 가장 왼쪽 열(시퀀스의 첫 번째 토큰에 해당)은 0이 아닌(그러나 변동하는) 값으로 완전히 채워져 있습니다. 이는 각 출력 토큰이 첫 번째 가치 토큰에 의해 어느 정도 영향을 받는다는 것을 의미합니다. 게다가 현재 토큰의 이웃과 초기 토큰 사이의 관심 점수의 지배력에는 부정확하지만 식별 가능한 진동이 있습니다. 이 진동 기간은 다양하지만 일반적으로 짧게 시작하여 시퀀스를 아래로 내려갈수록 길어집니다(마찬가지로 인과 관계가 주어지면 관련 행당 후보 주의 토큰 수와 관련됩니다). (attn @ V)가 어떻게 형성되는지 이해하려면 주의에만 집중하지 않는 것이 중요합니다. V도 마찬가지로 중요합니다. 각 출력 항은 전체 V 벡터의 가중 평균입니다. 주의가 완벽한 대각선인 극단적인 경우 attn @ V 는 V 의 정확한 복사본일 뿐입니다. 여기서 우리는 좀 더 질감이 있는 것을 볼 수 있습니다. 특정 토큰이 주의 행의 연속된 하위 시퀀스에서 높은 점수를 얻고 V와 분명히 유사하지만 대각선이 더 두꺼운 매트릭스에 겹쳐지는 가시적 밴드형 구조입니다. 일부 수직 폐색이 있습니다. (참고: mm 참조 가이드에 따르면 길게 누르거나 Ctrl 키를 누른 채 클릭하면 시각적 요소의 실제 숫자 값이 표시됩니다.) 우리는 중간 레이어(레이어 5)에 있으므로 이 어텐션 헤드에 대한 입력은 원래 토큰화된 텍스트가 아니라 중간 표현이라는 점을 기억하세요. 따라서 입력에서 볼 수 있는 패턴은 그 자체로 많은 생각을 불러일으킵니다. 특히 강한 수직선은 값이 시퀀스의 긴 구간에 걸쳐 균일하게 높은 진폭을 갖는 특정 임베딩 위치이며 때로는 거의 가득 찼습니다. 하지만 흥미로운 점은 입력 시퀀스의 첫 번째 벡터가 고유하다는 점입니다. 이러한 높은 진폭 열의 패턴을 깨뜨릴 뿐만 아니라 거의 모든 위치에서 비정형 값을 전달합니다(참고: 여기에서는 시각화되지 않았지만, 이 패턴은 여러 샘플 입력에서 반복적으로 나타납니다. 참고: 마지막 두 점과 관련하여 여기서 시각화되는 내용은 단일 샘플 입력에 대한 계산이라는 점을 다시 한 번 강조할 가치가 있습니다. 실제로 각 헤드에는 상당히 큰 샘플 세트에 걸쳐 일관되게(동일하지는 않지만) 표현되는 특징적인 패턴이 있는 것으로 나타났습니다. 그러나 활성화가 포함된 시각화를 볼 때 입력의 전체 분포를 기억해야 합니다. 그것이 영감을 주는 아이디어와 직관에 미묘한 방식으로 영향을 미칠 수 있습니다. 마지막으로 애니메이션을 직접 탐색해보는 것도 또 추천드려요! 4c Attention Heads에는 흥미로운 차이점이 많이 있습니다. 계속 진행하기 전에 모델이 어떻게 작동하는지 자세히 이해하기 위해 모델을 간단히 연구하는 것의 유용성을 보여주는 또 다른 데모가 있습니다. GPT-2의 또 다른 주목 헤드입니다. 그 동작 패턴은 레벨 5 머리 4의 동작 패턴과 상당히 다릅니다. 이는 모델의 매우 다른 부분에 있기 때문에 예상할 수 있는 것입니다. 이 헤더는 레벨 1: 헤드 2(레벨 0의 헤드 2)에 있습니다. 주목할 점: 이 헤더의 관심은 매우 고르게 분산되어 있습니다. 이는 애니메이션에 표시된 대로 V의 상대적 비가중 평균(또는 V의 적절한 인과 접두사)을 attn@V의 각 행에 전달하는 효과가 있습니다. 주의 점수 삼각형을 아래로 이동하면 attn[i] @ V; 벡터 - 단순히 축소된 V의 복사본이 아니라 변동이 작은 매트릭스 제품입니다. attn @ V는 놀라운 수직 균일성을 가지고 있습니다. 동일한 패턴의 값이 포함된 큰 원주형 영역의 시퀀스 전체에 걸쳐 지속됩니다. 이를 각 토큰이 공유하는 속성으로 생각할 수 있습니다. 참고: 한편으로는 주의가 매우 고르게 분산되는 효과를 고려할 때 attn @ V가 어느 정도 일관성을 가질 것이라고 기대할 수도 있습니다. 그러나 각 행은 전체 시퀀스가 아닌 V의 원인 하위 시퀀스로 구성됩니다. 시퀀스를 아래로 이동할 때 점진적인 변형과 같은 더 많은 변화가 발생하지 않는 이유는 무엇입니까? 육안 검사에 따르면 V는 길이에 따라 균일하지 않으므로 값 분포의 좀 더 미묘한 속성에 답이 있어야 합니다. 마지막으로 외부 투영 후 이 헤드의 출력은 수직 방향으로 더욱 균일해야 합니다. 우리는 강한 인상을 받을 수 있습니다. 이 어텐션 헤드가 전달하는 대부분의 정보는 시퀀스의 각 토큰이 공유하는 속성으로 구성됩니다. 출력 투영 가중치의 구성은 이러한 직관을 강화할 수 있습니다. 전반적으로 우리는 궁금해하지 않을 수 없습니다. 이 주의 머리가 생성한 극도로 규칙적이고 고도로 구조화된 정보는 약간... 덜 고급스러운 컴퓨팅 수단을 통해 얻은 것일 수도 있습니다. 이것은 확실히 미개척 영역은 아니지만, 계산 신호 시각화의 명확성과 풍부함은 새로운 아이디어를 생성하고 기존 아이디어에 대해 추론하는 데 매우 유용할 수 있습니다. 4d 소개로 돌아가기: 자유 불변 돌이켜 보면 반복할 필요가 있습니다. 주의 우선의 중요하지 않은 합성 연산을 시각화하고 이를 직관적으로 유지할 수 있는 이유는 매개변수와 같은 중요한 대수적 속성 때문입니다. 모양이 제한되거나 평행 축이 어떤 작업과 교차하는지) 이러한 속성은 추가 사고가 필요하지 않습니다. 기억해야 할 추가 규칙이 아니라 시각적 객체의 기하학적 속성에서 직접 발생합니다. 예를 들어, 이러한 주의 머리 시각화에서는 Q와 attn @ V의 길이가 같고, K와 V의 길이가 같고, 이 쌍의 길이는 각각 독립적이라는 것을 명확하게 알 수 있습니다. other; Q는 K와 너비가 같고, V는 attn @ V와 너비가 동일하며, 이 쌍의 너비는 서로 독립적입니다. 이러한 구조는 구조적으로 실제적이며 구조 구성 요소가 복합 구조에서 어디에 위치하고 방향이 무엇인지에 대한 간단한 결과입니다. 이 "자유로운 자연"의 장점은 일반적인 구조의 변형을 탐색할 때 특히 유용합니다. 확실한 예는 한 번에 자동 회귀 토큰에서 단일 행 높이 어텐션 매트릭스를 디코딩하는 것입니다. 5 병렬성 Attention 위 5개 레이어 중 4번째 헤드의 애니메이션은 어텐션 헤드의 6개 행렬 곱셈 중 4개를 시각화합니다. 벡터 매트릭스 제품의 융합 체인으로 시각화되어 기하학적 직관을 확인합니다. 입력에서 출력까지 전체 왼쪽 연결 체인은 공유 i축을 따라 계층화되며 병렬화될 수 있습니다. 5a 예: i를 따라 분할 실제로 계산을 병렬화하기 위해 입력을 i 축을 따라 청크로 분할할 수 있습니다. 주어진 축이 특정 수의 블록으로 분할되도록 지정하여 도구에서 이러한 분할을 시각화할 수 있습니다. 이 예에서는 8이 사용되지만 해당 숫자에는 특별한 것이 없습니다. 그 외에도 이 시각화에서는 각 병렬 계산에 전체 wQ(내부 투영용), K_t 및 V(주의용) 및 wO(외부 투영용)가 필요하다는 것을 명확하게 보여줍니다. 행렬: 5b 예: 이중 분할 여러 축에 따른 분할의 예도 여기에 나와 있습니다. 이를 위해 여기서는 Flash Attention과 같은 일부 연구 결과를 기반으로 하는 BPT(Block Parallel Transformer)라는 이 분야의 최근 혁신을 시각화하기로 선택했습니다. 논문을 참조하세요. https://arxiv.org/ pdf/2305.19370.pdf 우선 BPT는 위에서 설명한 대로 i를 따라 분할하며 실제로 시퀀스의 수평 분할을 주의 계층(FFN)의 나머지 절반까지 확장합니다. (이에 대한 시각화는 나중에 표시됩니다.) 이 컨텍스트 길이 문제를 완전히 해결하려면 MHA에 두 번째 파티션, 즉 주의 계산 자체의 파티션(즉, Q @ K_t의 j축을 따른 파티션)을 추가하세요. 이 두 파티션은 주의를 블록 그리드로 나눕니다. 이 시각화에서 알 수 있듯이: 이 이중 분할은 이제 각 발생의 시퀀스 길이를 시각적으로 나눌 수 있기 때문에 컨텍스트 길이 문제를 효과적으로 해결합니다. 주의 계산 중. 두 번째 분할의 "범위": 기하학적 구조에서 K와 V의 내부 투영 계산이 핵심 이중 행렬 곱셈과 함께 분할될 수 있다는 것이 분명합니다. 미묘한 세부 사항에 유의하세요. 여기서 시각적 힌트는 k를 따라 후속 행렬 곱셈 attn @ V를 병렬화하고 부분 결과를 분할-k 스타일로 합산하여 전체 이중 행렬 곱셈을 병렬화할 수도 있다는 것입니다. 그러나 sdpa()의 행별 소프트맥스에는 요구 사항이 추가됩니다. 즉, 각 행은 attn@V의 해당 행을 계산하기 전에 모든 세그먼트 정규화를 가져야 하며, 이는 추가 라인별 단계를 추가합니다. 6 Size of Attention Layer Attention 레이어(MHA)의 전반부는 2차 복잡도로 인해 계산 요구 사항이 높은 것으로 알려져 있지만, FFN(후반부)에도 고유한 요구 사항이 있습니다. 이는 일반적으로 모델에 포함된 차원 너비의 4배인 숨겨진 차원의 너비 때문입니다. 완전한 Attention 레이어의 바이오매스를 시각화하면 레이어의 두 절반이 서로 비교되는 방식을 직관적으로 이해하는 데 도움이 됩니다. 6a 완전한 Attention 레이어 시각화 아래는 완전한 Attention 레이어이며, 전반부(MHA)가 뒤쪽에 있고 후반부(FFN)가 앞쪽에 있습니다. 이번에도 화살표는 계산 방향을 가리킵니다. 참고: 이 시각화는 단일 주의 머리를 묘사하지 않지만 중앙 이중 행렬 곱셈 주위의 분할되지 않은 Q/K/V 가중치 및 투영을 보여줍니다. 물론 이는 전체 MHA 작업을 충실하게 시각화하지는 않습니다. 그러나 여기서 목표는 각 절반에서 수행되는 상대적 계산량이 아닌 레이어의 두 절반에서 상대적인 행렬 크기에 대한 더 명확한 아이디어를 얻는 것입니다. (또한 여기의 가중치는 실제 가중치 대신 임의의 값을 사용합니다.) 여기에 사용된 크기는 브라우저가 (상대적으로) 전달할 수 있도록 축소되었지만 비율은 동일하게 유지됩니다(NanoGPT의 작은 구성에서) ): 모델 임베딩 차원 = 192(원래 768), FFN 임베딩 차원 = 768(원래 3072), 시퀀스 길이 = 256(원래 1024)이지만 시퀀스 길이는 모델에 근본적인 영향을 미치지 않습니다. (시각적으로 시퀀스 길이의 변화는 입력 블레이드 너비의 변화로 나타나 주의 중심 크기 및 하류 수직 평면 높이의 변화로 이어집니다.) 6b BPT 분할 레이어 시각화 간단히 되돌아보기 Blockwise Parallel Transformer는 전체 Attention 레이어의 맥락에서 BPT를 시각화하는 병렬화 방식입니다(위에서 헤더는 생략됨). 특히 i(시퀀스 블록)에 따른 분할이 MHA 및 FFN 절반을 통해 어떻게 확장되는지 확인하세요. 6c FFN 분할 이 시각화 방법은 위에서 설명한 것과 직교하는 추가 파티션을 제안합니다. 즉, attention 레이어의 FFN 절반에서 이중 행렬 곱셈(attn_out @ FFN_1) @ FFN_2를 먼저 j attn_out @ FFN_1을 따라 분할한 다음 후속 행렬 곱셈을 수행합니다. FFN_2와 함께 k를 따라갑니다. 이 분할은 부분 결과의 최종 합계를 희생하면서 계산에 참여하는 각 구성 요소의 용량 요구 사항을 줄이기 위해 두 개의 FFN 가중치 계층을 분할합니다. 분할되지 않은 Attention 레이어에 이 분할 방법을 적용하면 다음과 같습니다. BPT로 분할된 레이어에 적용하면 다음과 같습니다. 6d 시각화 한 번에 하나의 토큰 디코딩 process 자동회귀형 한 번에 하나의 토큰 디코딩 프로세스에서 쿼리 벡터는 단일 토큰으로 구성됩니다. 이 경우 주목 레이어가 어떤 모습일지 상상해 보는 것은 유익합니다. 즉, 거대한 타일로 배열된 가중치 평면을 가로지르는 단일 임베딩 행입니다. 활성화에 비해 가중치가 크다는 점을 강조하는 것 외에도, 이 관점은 Mux/Demux 계산으로 인해 이러한 대응이 부정확해질 수 있음에도 불구하고 K_t 및 V가 6계층 MLP에서 동적으로 생성된 계층과 유사하게 작동한다는 개념을 상기시킵니다. 7 LoRA 최근 LoRA 논문 "LoRA: Low-Rank Adaptation of Large Language Models"는 다음 아이디어에 기반한 효율적인 미세 조정 기술을 설명합니다. 미세 조정 중에 도입된 가중치 δ는 낮은 순위입니다. . 논문에 따르면, 이를 통해 "적응 중 조밀한 계층 변경의 순위 분해 행렬을 최적화함으로써 사전 훈련된 가중치를 고정한 상태로 유지함으로써 신경망의 일부 조밀한 계층을 간접적으로 훈련할 수 있습니다." 아이디어 간단히 말해서 핵심 단계는 행렬 자체가 아닌 가중치 행렬의 요소를 훈련하는 것입니다. I x J 가중치 텐서를 I x K 텐서 및 K x J 텐서의 행렬 곱셈으로 대체합니다. K가 작은 값인지 확인하세요. LoRA가 이 분해 방법을 미세 조정 프로세스에 적용하는 방식은 다음과 같습니다. 각 가중치에 대해 



 직관력을 구축하기 위해 벡터-행렬 곱을 사용하는 또 다른 방법이 있습니다. 예, 이는 단위 행렬이 해당 매개변수와 결과를 반영하여 45도 각도로 배치된 거울처럼 작동함을 보여줍니다.
직관력을 구축하기 위해 벡터-행렬 곱을 사용하는 또 다른 방법이 있습니다. 예, 이는 단위 행렬이 해당 매개변수와 결과를 반영하여 45도 각도로 배치된 거울처럼 작동함을 보여줍니다. 










Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
sdpa (input @ wQ @ K_t) @ V @ wO










 7b LoRA를 어텐션 헤드에 적용합니다.
7b LoRA를 어텐션 헤드에 적용합니다.
위 내용은 3D 관점에서 행렬 곱셈에 대한 통찰력, 이것이 AI 사고의 모습입니다의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
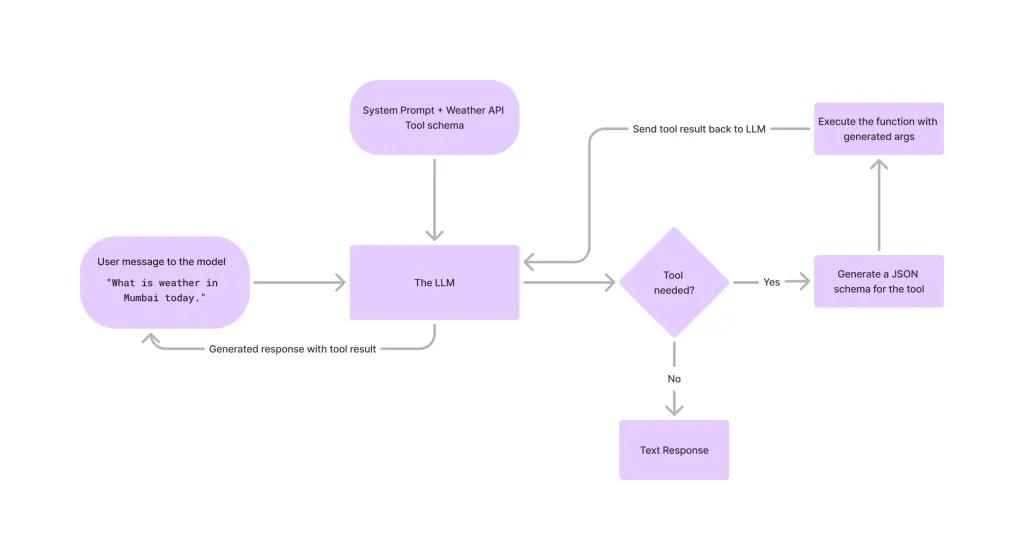 LLM에서 도구 호출Apr 14, 2025 am 11:28 AM
LLM에서 도구 호출Apr 14, 2025 am 11:28 AM대형 언어 모델 (LLM)은 인기가 높아졌으며, 도구 전달 기능은 단순한 텍스트 생성을 넘어 기능을 극적으로 확장했습니다. 이제 LLM은 동적 UI 생성 및 자율적 인 A와 같은 복잡한 자동화 작업을 처리 할 수 있습니다.
 ADHD 게임, 건강 도구 및 AI 챗봇이 글로벌 건강을 변화시키는 방법Apr 14, 2025 am 11:27 AM
ADHD 게임, 건강 도구 및 AI 챗봇이 글로벌 건강을 변화시키는 방법Apr 14, 2025 am 11:27 AM비디오 게임이 불안을 완화하거나 집중하거나 ADHD를 가진 어린이를 지원할 수 있습니까? 건강 관리 도전이 전 세계적으로 급증함에 따라, 특히 청소년들 사이에서 혁신가들은 비디오 게임 인 가능성이없는 도구로 전환하고 있습니다. 이제 세계 최대의 엔터테인먼트 인더스 중 하나입니다
 AI에 대한 UN 입력 : 우승자, 패자 및 기회Apr 14, 2025 am 11:25 AM
AI에 대한 UN 입력 : 우승자, 패자 및 기회Apr 14, 2025 am 11:25 AMUNCTAD의 사무 총장 인 Rebeca Grynspan은“역사는 기술 진보가 경제 성장을 유발하거나 공평한 소득 분배를 보장하거나 포용적인 인간 발전을 촉진하지는 않습니다.
 생성 AI를 통한 협상 기술 학습Apr 14, 2025 am 11:23 AM
생성 AI를 통한 협상 기술 학습Apr 14, 2025 am 11:23 AM쉽게 생성 AI를 협상 교사 및 스파링 파트너로 사용하십시오. 그것에 대해 이야기합시다. 혁신적인 AI 혁신에 대한이 분석은 AI의 최신 Forbes 열 범위의 일부입니다.
 Ted는 Openai, Google, 메타가 법정으로 공개됩니다.Apr 14, 2025 am 11:22 AM
Ted는 Openai, Google, 메타가 법정으로 공개됩니다.Apr 14, 2025 am 11:22 AM밴쿠버에서 개최 된 TED2025 컨퍼런스는 어제 4 월 11 일 36 번째 판을 마무리했습니다. Sam Altman, Eric Schmidt 및 Palmer Luckey를 포함한 60 개 이상의 국가에서 80 명의 스피커를 선보였습니다. 테드의 주제 인“인류를 다시 상상했다”는 재단사가 만들어졌다
 Joseph Stiglitz는 AI 독점권 속에서 임시 불평등을 경고합니다.Apr 14, 2025 am 11:21 AM
Joseph Stiglitz는 AI 독점권 속에서 임시 불평등을 경고합니다.Apr 14, 2025 am 11:21 AMJoseph Stiglitz는 2001 년에 유명한 경제학자이자 노벨 경제학상을 수상했습니다. Stiglitz는 AI가 기존의 불평등과 통합 된 권력을 몇몇 지배적 인 기업의 손에 악화시킬 수 있으며 궁극적으로 경제를 훼손 할 수 있다고 주장합니다.
 그래프 데이터베이스 란 무엇입니까?Apr 14, 2025 am 11:19 AM
그래프 데이터베이스 란 무엇입니까?Apr 14, 2025 am 11:19 AM그래프 데이터베이스 : 관계를 통한 데이터 관리 혁명 데이터가 확장되고 그 특성이 다양한 필드에서 발전함에 따라 그래프 데이터베이스는 상호 연결된 데이터를 관리하기위한 변환 솔루션으로 떠오르고 있습니다. 전통적인 것과는 달리
 LLM 라우팅 : 전략, 기술 및 파이썬 구현Apr 14, 2025 am 11:14 AM
LLM 라우팅 : 전략, 기술 및 파이썬 구현Apr 14, 2025 am 11:14 AM대형 언어 모델 (LLM) 라우팅 : 지능형 작업 분포를 통한 성능 최적화 LLM의 빠르게 진화하는 환경은 각각 독특한 강점과 약점을 가진 다양한 모델을 제시합니다. 일부는 Creative Content Gen에서 탁월합니다


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

SublimeText3 영어 버전
권장 사항: Win 버전, 코드 프롬프트 지원!

안전한 시험 브라우저
안전한 시험 브라우저는 온라인 시험을 안전하게 치르기 위한 보안 브라우저 환경입니다. 이 소프트웨어는 모든 컴퓨터를 안전한 워크스테이션으로 바꿔줍니다. 이는 모든 유틸리티에 대한 액세스를 제어하고 학생들이 승인되지 않은 리소스를 사용하는 것을 방지합니다.

ZendStudio 13.5.1 맥
강력한 PHP 통합 개발 환경

Dreamweaver Mac版
시각적 웹 개발 도구

드림위버 CS6
시각적 웹 개발 도구






