주어진 이진 트리에서 가장 큰 이진 검색 하위 트리 찾기 - C++의 에피소드 1
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-08-31 15:33:07731검색
이 문제에는 이진 트리 BT가 주어졌습니다. 우리의 임무는 주어진 이진 트리에서 가장 큰 이진 검색 하위 트리를 찾는 것입니다.
바이너리 트리는 데이터 저장에 사용되는 특수한 데이터 구조입니다. 이진 트리에는 각 노드가 최대 2개의 하위 노드를 가질 수 있다는 특별한 조건이 있습니다.
BST(이진 검색 트리)는 다음 속성을 만족하는 트리입니다.
왼쪽 하위 트리의 키 값은 상위 노드(루트 노드)의 키 값보다 작습니다.
오른쪽 하위 트리의 키 값은 상위 노드(루트 노드)의 키 값보다 크거나 같습니다.
이 문제를 이해하기 위해 예를 들어 보겠습니다.
Input:
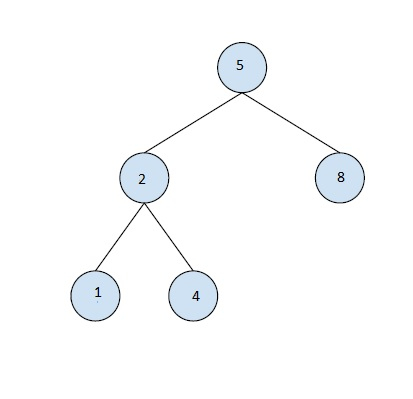
Output: 3
Explanation
Full binary tree is a BST.
Solution
~을 해라 트리 진행 중 순서 순회. 트리의 각 노드에 대해 하위 트리가 이진 검색 트리인지 확인합니다. 마지막으로 가장 큰 이진 검색 하위 트리의 크기가 반환됩니다.
Example
우리 솔루션의 작동 방식을 보여주는 프로그램의 예
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findTreeSize(node* node) {
if (node == NULL)
return 0;
else
return(findTreeSize(node->left) + findTreeSize(node->right) + 1);
}
int isBSTree(struct node* node) {
if (node == NULL)
return 1;
if (node->left != NULL && node->left->data > node->data)
return 0;
if (node->right != NULL && node->right->data < node->data)
return 0;
if (!isBSTree(node->left) || !isBSTree(node->right))
return 0;
return 1;
}
int findlargestBSTSize(struct node *root) {
if (isBSTree(root)){
return findTreeSize(root);
}
else
return max(findlargestBSTSize(root->left), findlargestBSTSize(root->right));
}
int main() {
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The size of the largest possible BST is "<<findlargestBSTSize(root);
return 0;
}Output
The size of the largest possible BST is 5
또 다른 접근 방식
이 문제를 해결하는 또 다른 방법은 아래쪽에서 트리를 순회하고 하위 노드를 통해 확인하는 것입니다. BST. 이를 위해 다음을 추적합니다.
가 BST인지 여부.
왼쪽 하위 트리의 경우 가장 큰 요소의 값입니다.
오른쪽 하위 트리의 경우 가장 작은 요소의 값입니다. BST를 확인하려면 이 값을 현재 노드와 비교해야 합니다.
또한 최대 BST 크기는 현재 BST 크기와 비교하여 업데이트됩니다.
예
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findlargestBSTSizeRec(node* node, int *minValRsubTree, int *maxValLsubTree, int *maxBSTSize, bool *isBSTree) {
if (node == NULL){
*isBSTree = true;
return 0;
}
int min = INT_MAX;
bool left_flag = false;
bool right_flag = false;
int leftSubtreeSize,rightSubTreeSize;
*maxValLsubTree = INT_MIN;
leftSubtreeSize = findlargestBSTSizeRec(node->left, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data > *maxValLsubTree)
left_flag = true;
min = *minValRsubTree;
*minValRsubTree = INT_MAX;
rightSubTreeSize = findlargestBSTSizeRec(node->right, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data < *minValRsubTree)
right_flag = true;
if (min < *minValRsubTree)
*minValRsubTree = min;
if (node->data < *minValRsubTree)
*minValRsubTree = node->data;
if (node->data > *maxValLsubTree)
*maxValLsubTree = node->data;
if(left_flag && right_flag){
if (leftSubtreeSize + rightSubTreeSize + 1 > *maxBSTSize)
*maxBSTSize = (leftSubtreeSize + rightSubTreeSize + 1);
return (leftSubtreeSize + rightSubTreeSize + 1);
}
else{
*isBSTree = false;
return 0;
}
}
int findlargestBSTSize(node* node){
int min = INT_MAX;
int max = INT_MIN;
int largestBSTSize = 0;
bool isBST = false;
findlargestBSTSizeRec(node, &min, &max, &largestBSTSize, &isBST);
return largestBSTSize;
}
int main(){
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The Size of the largest BST is "<<findlargestBSTSize(root);
return 0;
}출력
The Size of the largest BST is 5
위 내용은 주어진 이진 트리에서 가장 큰 이진 검색 하위 트리 찾기 - C++의 에피소드 1의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

