엑셀 함수 학습: LOOKUP 함수의 이분법적 원리

이전 글 "Excel 함수 학습: LOOKUP 함수를 사용하는 5가지 방법"에서 LOOKUP 함수를 사용하는 5가지 방법에 대해 알아보았습니다. 많은 친구들이 이해하지 못한 것 같습니다. 오늘은 두 부분을 설명하겠습니다. LOOKUP의 원리를 자세히 이해한 후에는 어제의 튜토리얼을 다시 읽어보시면 LOOKUP에 대한 이해가 달라질 것이라고 믿습니다.

이전 글에서는 LOOKUP 함수의 다양한 루틴에 대해 알아보았고, LOOKUP 함수의 검색이 이분법 방식에 기반을 두고 있다고 여러 번 언급했습니다. 그렇다면 오늘은 이분법에 대해 알아보겠습니다. 이 질문입니다.

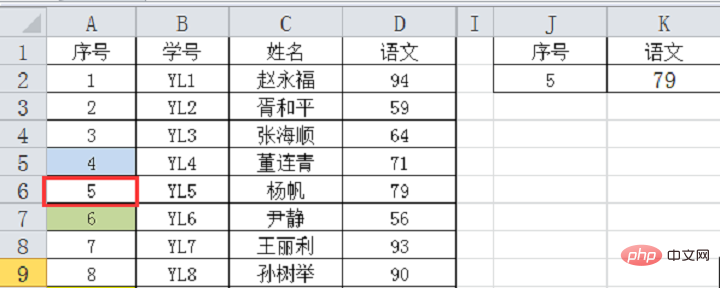
어제의 예를 계속 사용해 보겠습니다. 일련 번호로 결과를 검색하면 일련 번호가 오름차순이며 수식 =LOOKUP(J2,A2:D19)의 결과가 정확합니다.

1. 이진 검색의 원리

이진 검색은 검색 범위의 데이터를 숫자에 따라 둘로 나누어 중간 위치, 중간 값에 있는 데이터를 찾은 후 이를 사용하는 것입니다. 우리의 검색 값을 중간 값과 비교하십시오. 중간값이 검색값과 같으면 바로 결과를 구하고, 중간값이 검색값보다 작으면 아래쪽으로 이진 검색 비교를 계속한다. 중간 값을 제외한 데이터), 중간 값이 검색 값보다 큰 경우 위쪽으로 이진 검색 비교가 계속됩니다(즉, 중간 값을 제외한 데이터의 상위 절반에서 이진 검색이 계속됩니다). 마지막 데이터까지 이분화하여 검색한 값과 일치하는 데이터가 없는 경우: 마지막 데이터가 검색한 값보다 작으면 마지막 데이터가 검색한 값보다 크면 마지막 데이터의 위치를 ​​이용하여 결과값을 구합니다. 검색값을 입력한 후 위쪽으로 검색합니다. 마지막 데이터와 가장 가까운 위치의 데이터가 검색값보다 작거나 같으면 이 데이터의 위치를 ​​기준으로 결과를 구합니다.

이것은 단지 설명일 뿐이며 많은 친구들이 헷갈릴 것 같습니다. 위의 예를 결합하여 일련번호 5를 통해 중국어 점수 79를 찾는 방법을 자세히 살펴보겠습니다.

첫 번째 비교: 검색 범위 A2~A19에 18개의 데이터가 있고, 중간 위치는 18¼2=9, 즉 셀 A10의 중간 값이 9입니다. 당연히 검색값 5는 9보다 작으므로 계속 A2~A9 위쪽으로 검색하세요

팁: 검색 범위의 데이터 개수가 홀수이면 중간 위치는 (숫자 + 1) ¼ 2입니다. 예를 들어, 행이 11개인 경우 중간 위치는 (11+1)nn2=6이고, 데이터 개수가 짝수인 경우 중간 위치는 (숫자)‐2입니다.

두 번째 비교: 데이터는 8개뿐이고 중간 위치는 8¼2=4, 셀 A5의 중간 값은 4, 검색 값 5가 4보다 크므로 A6에서 계속 아래로 검색하세요~ A9. 참고로 현재 아래 숫자는 4개뿐이며, 9 이하의 데이터는 1차 검색에서 바로 제외됩니다.

세 번째 비교: 데이터 4개, 가운데 값이 A7의 6, 검색값 5가 6보다 작으므로 위쪽으로 검색하세요. 이때, 셀 A6에는 검색값과 일치하는 데이터 1개(5)만 남아 있으므로 5에 해당하는 D열의 데이터 79가 획득된다.

이러한 예만으로는 이분법을 이해하기가 매우 어렵습니다. 위 표의 데이터를 점수 내림차순으로 배열하거나, 일련번호 5로 중국어 점수를 검색해 보세요. 수식은 수정할 필요가 없습니다. 일련번호 열의 순서가 틀려 오름차순으로 정렬되지 않아서 실제 숫자는 79인데 수식으로는 94가 나오네요. 무슨 일이죠? 이분법을 통해 살펴보겠습니다.

첫 번째 검색: 중간 값(9번째 데이터)이 18이고, 검색 값 5가 18보다 작으므로 A2~A9에서 위쪽으로 검색합니다.

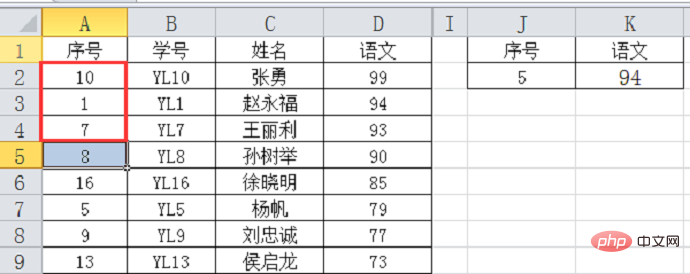
두 번째 검색: 위 8개의 데이터, 중간; 값(4번째 데이터)은 8이고, 검색값 5는 8보다 작으며, A2~A4에서 계속 위쪽으로 검색합니다.

세 번째 검색: 위 3개 데이터, 중간값이 1, 검색; 값 5가 1보다 큽니다. 아래쪽으로 검색:

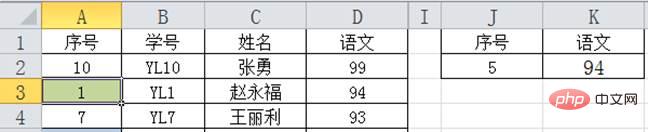
네 번째 검색: 이제 A4 셀에 데이터 7이 하나만 있고 검색 값 5가 7보다 작으므로 7을 기준으로 위치를 찾습니다. 7에 가장 가깝고 값이 5보다 작거나 5와 같은 데이터는 셀 A3에 1이고 얻은 해당 중국어 값은 94입니다.

이 두 가지 예를 통해 모든 사람이 이분법에 대해 어느 정도 이해해야 한다고 생각합니다. 이 원칙과 관련하여 함수 설명에는

한 문장만 있습니다.

실제 응용에서 우리는 이분법이 무엇인지, 중간 위치가 무엇인지, 아래를 내려다볼 것인지 아니면 위를 볼 것인지에 대해 걱정할 필요가 없습니다. 이것은 모두 함수의 작업이며, 우리는 한 가지만 기억하면 됩니다: 데이터는 오름차순으로 정렬되어야 합니다. 오름차순으로 정렬할 수 없는 경우 LOOKUP의 정확한 검색 루틴을 따라 수식을 디자인하세요.

2. LOOKUP은 데이터 반올림을 구현합니다.

이것이 이분법 원리에 대한 소개입니다. 다음으로, 앞서 남겨진 두 가지 문제를 해결해야 합니다.

5월 12일 기사에서는 반올림 문제를 해결하기 위해 LOOKUP을 사용했는데, 그 결과 모두가 설명을 요청하는 메시지를 남겼습니다.

그렇다면 모두의 열띤 토론을 불러일으킨 이 공식은 무엇일까요? 아래 그림을 보세요.

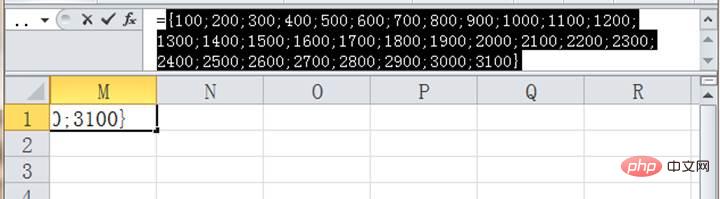
이 수식은 LOOKUP 함수를 사용하여 100번째 자리 이하의 모든 숫자를 반올림하여 백분위수 반올림을 달성하는 것으로 나타났습니다.

이분법의 원리를 이해했다면 이제 LOOKUP이 이를 모두에게 설명할 차례입니다. 먼저 ROW (A:A)*100 부분을 설명해주세요. 실제로는 일련의 숫자를 가져옵니다. 모두가 이해할 수 있도록 A:A의 범위를 더 작게 만들어 =ROW(A1:A31)*100을 설명으로 사용합니다.

셀에는 100이 하나만 표시되지만 실제로는 31개의 숫자, f9 기능 키를 사용하여 특정 내용을 볼 수 있습니다.

ROW 함수는 셀의 행 번호를 얻는 데 사용됩니다. ROW(A1:A31)*100에 다음의 행 번호를 곱합니다. 셀 A1부터 A31까지 100을 사용하여 수백 자리 {100;200;300;...3000;3100}으로 반올림된 데이터 세트를 얻습니다.

그리고 LOOKUP이 무대에 올랐습니다. 위에서 얻은 수백 자리로 반올림된 배열에서 A1을 검색합니다. 배열이 오름차순으로 배열되어 있기 때문에 A1을 찾는 핵심은 배열에서 A1보다 작거나 같은 최대값을 찾는 것입니다.

2517.32를 예로 들면 2500만이 그보다 작은 최대값이므로 결과는 2500이 됩니다. 관심이 있는 친구들은 이분법적 원리를 이용해 그것이 맞는지 스스로 확인해 볼 수 있습니다.

다른 숫자를 찾을 때도 마찬가지입니다. 이 공식이 영리한 이유는 반올림 문제를 참조 찾기 문제로 바꾸기 때문입니다. 정말 훌륭합니다!

3. 데이터 추출을 위한 LOOKUP

데이터 추출을 위해 다시 LOOKUP을 사용해서 5000단어 약속을 잡았습니다.

이번에는 무엇이 문제인가요? 원래 질문은 그림과 같이 학번을 추출합니다.

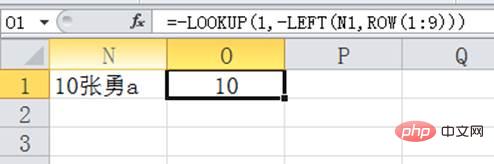
위 그림의 첫 번째 데이터를 사용하여 설명하겠습니다. 셀 N1에 "10 Zhang Yong a"를 입력한 후 셀 O1에 수식 =-LOOKUP(1,-LEFT(N1,ROW(1:9)))을 입력하여 학생 번호를 추출합니다.

LOOKUP은 참조 함수가 아닌데 어떻게 숫자를 다시 추출할 수 있나요?

LEFT 함수의 두 번째 매개 변수는 배열을 사용하며 ROW(1:9)는 {1;2;3;4;5;6;7;8;9}와 동일합니다. LEFT는 첫 번째 매개변수에 지정된 데이터를 왼쪽부터 추출하고, 추출 길이는 두 번째 매개변수에 따라 결정됩니다. LEFT는 배열 {1;2;3;4;5;6;7;8;9}에 따라 추출하여 9개의 결과를 얻습니다:

, 즉 왼쪽에서 숫자 1을 추출하고, 숫자 2를 추출합니다. .9비트까지. LEFT로 추출한 결과는 모두 텍스트 유형이므로 LEFT 앞에 음수 기호를 추가하면 텍스트 숫자가 숫자 값으로 변환될 수 있으며 해당 텍스트는 오류 값이 됩니다.

오류 값은 LOOKUP에서 무시되며, 이제 그것은 {-10}에서 1을 찾는 것이 됩니다. 1은 이 데이터 집합보다 큽니다. 이진 검색의 원리에 따르면, 이분법 후에는 마지막 숫자가 1보다 작아질 때까지만 아래쪽으로 검색할 수 있습니다. 따라서 검색 범위 내 모든 데이터보다 검색 값이 큰 경우(오름차순 여부에 관계없이) LOOKUP의 본질은 마지막 데이터를 찾는 것이라고 간단히 이해할 수 있습니다.

실제로 0은 모든 음수보다 크기 때문에 수식에서 1을 0으로 변경하는 것도 가능합니다.

현재 마지막 숫자는 -10이므로 앞에 음수 기호를 추가합니다. LOOKUP을 하면 10이 되는데, 이는 우리가 추출해야 할 숫자입니다.

초보자의 경우 위 두 가지 경우의 LOOKUP 사용법은 너무 고급입니다. 이러한 소개를 통해서도 실제로 기능을 이해하는 과정이 거의 없는 것으로 추정됩니다. 이해부터 숙달까지, 여기에는 많은 연습과 생각이 필요합니다. 모두가 긍정적이고 낙관적인 태도를 유지하고 학습 기능의 재미를 경험할 수 있다면 성공은 멀지 않습니다.

관련 학습 권장 사항: excel 튜토리얼

위 내용은 엑셀 함수 학습: LOOKUP 함수의 이분법적 원리의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!