ホームページ >テクノロジー周辺機器 >AI >AIはフェルマーの最終定理を克服できるか?数学者は100ページの証明をコードに変えるために5年間のキャリアを放棄した
AIはフェルマーの最終定理を克服できるか?数学者は100ページの証明をコードに変えるために5年間のキャリアを放棄した
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2024-04-09 15:20:02837ブラウズ
フェルマーの最終定理は AI によって征服されようとしていますか?
そして、全体の中で最も意味のある部分は、AI が解決しようとしているフェルマーの最終定理は、まさに AI が役に立たないことを証明することであるということです。
かつて、数学は純粋な人間の知性の領域に属していましたが、現在、この領域は高度なアルゴリズムによって解読され、踏みにじられています。
 写真
写真
フェルマーの最終定理は、何世紀にもわたって謎に包まれてきた「悪名高い」パズルであり、数学者を悩ませています。
それは 1993 年に証明され、現在数学者たちは素晴らしい計画を立てています。それは、コンピューターを使用して証明プロセスを再現するというものです。
彼らは、このバージョンの証明で、論理的なエラーがある場合、コンピューターでチェックできることを望んでいます。
プロジェクトアドレス: https://github.com/riccardobrasca/flt3
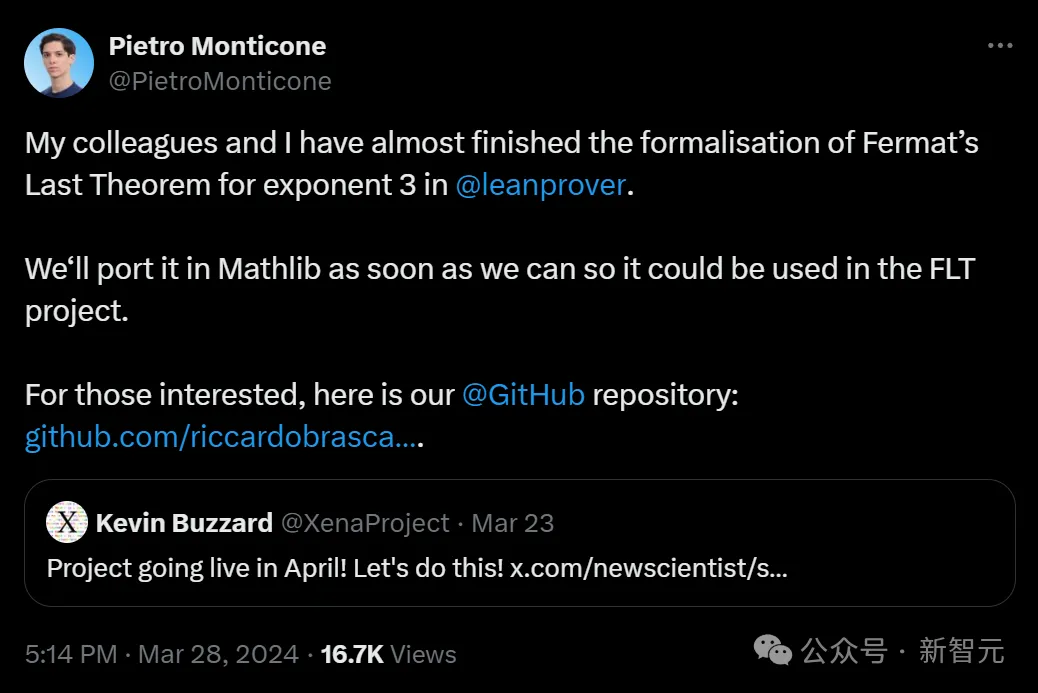
3月末, 数学者のピエトロ・モンティコーネは、自分と同僚がリーンプルーバーの指数3を使ったフェルマーの最終定理の定式化をほぼ完了したと興奮気味に語った。
彼らは、FLT プロジェクトで使用できるよう、できるだけ早く正式なプロセスを Mathlib に移植する予定です。
 写真
写真
証明プロセスは大まかにワイルズの証明に従いますが、わずかに変更があります。
Lean を使用してフェルマーの最終定理をコードに記述する
4 月になると、数学者でプログラマーの Kevin Buzzard がこの計画を発表します: 証明を完了するコンピューター コードによるフェルマーの最終定理の解明。
プロジェクトが 4 月にオンラインになった後、公開ブループリントがオンラインに表示されます。その時点で、リーン コミュニティの誰もが正式な証明に独自に貢献できます。
 写真
写真
画期的な 100 ページの数学的証明をコンピューター コードに変換するのは簡単ですか?
これはもちろん、テレンス・タオ氏が高く評価し愛用している証明ツール Lean のおかげです。このツールを使用すると、ユーザーは散文形式の証明をテスト用のルールとロジックに変換できます。 。
 写真
写真
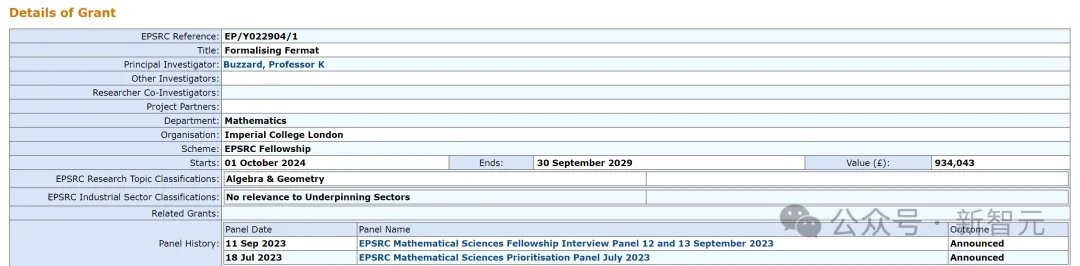
しかし、いずれにせよ、このプロジェクトは単純ではなく、何年もかかることが予想されます。ケビン・バザードのページプロジェクトの資金援助を獲得しました。
 写真
写真
このプロジェクトがおそらくこれまでで最も複雑なコンピューター化されたデモンストレーションの 1 つであることは誰もが理解しています。
 写真
写真
フェルマーの最終定理
フェルマーの最終定理、と呼ぶにふさわしい歴史上最もエキサイティングな数学パズルの 1 つ。
フェルマーの最終定理を証明するプロセスは、そのまま数学の歴史です。
 写真
写真
おなじみのフェルマーの最終定理は、17 世紀のフランスの数学者ピエール ド フェルマーによって発明され、マーが提案しました。残念ながら、彼は生前に証拠を見つけることができませんでした。
その結果、300 年以上前に始まったこの問題は、3 世紀にわたって人類に直接の課題を与え、世界に何度も衝撃を与え、人類の最も優れた頭脳のエネルギーを使い果たし、何百万ものアマチュアが残されました。それに夢中になっている。
 図
図
この定理は、方程式 (a^ を満たす 3 つの正の整数 a、b、c は存在しない) を主張します。 n b ^n = c^n)、n は 2 より大きい任意の整数です。
この証明の難しさは、数学者にとって負の場合を見つけるのが難しいことです。この方程式を満たす無限の整数 n が存在しないことをどのように保証できるでしょうか?
 写真
写真
幸いなことに、今日の数学者にとって、無限の概念を論理に変換することは何も新しいことではありません。もう終わりです。
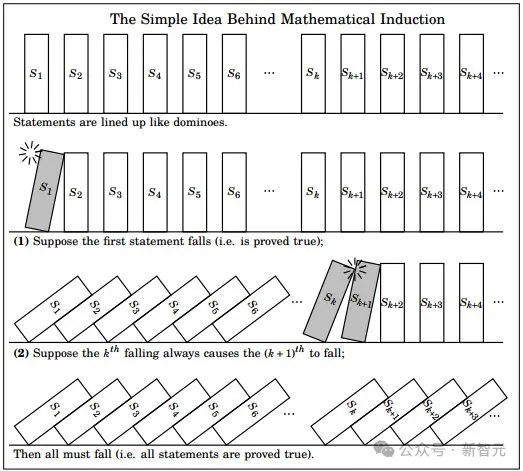
より単純な証明では、帰納法に頼ることができます。 -
特定のロジックが特定の数値 ( 8 など) に対して成立すると、これは、無限大までの後続のすべての数字 (9、10、11 など) にも当てはまります。
 写真
写真
しかし、フェルマーの最終定理は、数百年にわたって数学界の障害となってきました。
1993 年まで、英国の数学者アンドリュー ワイルズは、100 ページの書面による証明でこの謎を解決しました。
 写真
写真
コンピュータはなぜフェルマーの最終定理を証明できないのでしょうか?
#業界は 3 つの理由があると考えています:
1. コンピューターは無限の種を推定することはできません
2. コンピュータは論理が正しいことを証明できない
3. コンピュータは一時的な間違いを犯す可能性があります
幸いなことに、無駄のない補助証明があります
#100 ページの数学的証明は、一般の数学の学生や数学者にとってそれほど簡単ではありません。幸いなことに、私たちはもはや従来の証明方法に頼ることはできず、Lean のようなツールに頼ることができます。
これは、帰納証明の作成と検証のために設計された C ベースのプログラミング ツールです。
今日のいわゆる「人工知能」の多くは、人間の言語を模倣して巧妙に配置された言葉にすぎません。しかし、Lean などのコンピューター支援証明は、人間の思考とコンピューター支援による拡張機能をより深く統合します。
写真
リーンプログラミングツール、学部教室への参入
Imperialロンドン工科大学で数学を教えている Kevin Buzzard 氏は、大学の学部数学カリキュラム全体で Lean を使用したサポート ツールの開発に数年を費やしました。これらのツールを通じて、学生は授業で議論された内容を論理的および数学的なステップに分解できます。
これは数学的証明のロゼッタストーンのようなものです。
数学教師でもあるクラリッサ・リトラーは、ケビン・バザードの哲学に強く同意します。
彼女はポートランド コミュニティ カレッジで離散数学を教えています。過去 2 学期、彼女は離散数学のクラスで Kevin Buzzard が開発した「リーン クラシック入門ゲーム」を使用しました。
写真
彼女は、「自然数ゲーム」を使用して生徒が数学的帰納法の考え方に慣れるのを助け、「集合論ゲーム」を通じて、集合についての推論に慣れさせます。 #このプロセスでは、学生は「論理的なルールに厳密に従って証明を書くこと」と「一般的な言語を使用すること」について学びました。言語 「物事の真実を説明する」ことの間の理解のギャップは徐々に埋められます。 リトラー教授は、このコースの主な焦点は、数学の基礎が弱い生徒が数学者のやり方でより自由に考えることができるようにすると同時に、証明、証拠、方法をよりよく理解できるようにすることであると強調しました。真実を証明するために。 形式論理からルールのリスト、そして散文へのこの移行は、プロジェクトを連携するコード部分に分割するための鍵となります。 これは、プログラミングと純粋数学の交差点で特に重要であり、それはまさに Lean A のようなツールです輝ける場所。 バザード氏は、フェルマーの最終定理からインスピレーションを得た複雑な数学的アイデアをプログラム可能な形式に変換したいと述べました。 何世紀にもわたって、この定理を証明するために、数学の多くの貴重な新しい分野が作成されてきましたが、バザード氏の意見では、この定理は「実用的には重要ではない」とのことです。 はい、バザードの見解では、フェルマーの最終定理は無意味であり、現実世界には何の応用もありません。しかし、この「悪名高い」問題のせいで、何人かの実践的な人々が大量のコードを生成しています。素晴らしい新しいアイデア。 さて、ワイルズの 100 ページの証明をコンピュータが理解できる形式言語と規則に変換することで、新世代の数学者にコンピュータ支援証明への扉が開かれることが期待されています。 この変換ツールはプログラマーにも役立ちます。 Littler 氏は、この分野では、学んだ教訓や作成されたライブラリから誰もが恩恵を受けることができるため、野心的なプロジェクトには常に挑戦する価値があると述べました。 インタラクティブな定理証明はまだ比較的新しい分野ですが、リーン コミュニティは多くの優れた研究を行ってきました。 Kevin Mark Buzzard は 1968 年生まれで、数論幾何学とラングランズ プログラムに関する深い専門知識を持っています。 彼は現在、インペリアル カレッジ ロンドンの純粋数学の教授であり、AI ツール Lean の「伝道者」です。 ケビン バザードは、ロイヤル グラマー スクール在学中に国際数学オリンピックに参加し、1986 年に銅メダル、1987 年に満点で金メダルを獲得しました。 その後、ケンブリッジ大学トリニティ カレッジで数学の学部課程を修了し、1990 年に上級学位を授与されました。ラングラーのタイトルを獲得し、1991 年に C.A.S.M. の学位を取得しました。 リチャード・テイラーの監督のもと、彼の博士論文「モジュラー表現のレベル」は 1995 年に完成し、数学の複雑な領域を探求しました。 1998 年にインペリアル カレッジ ロンドンで講師として働き始め、2002 年に上級講師に昇進しました。 2004年に上級講師に昇進し、教授に就任。 彼はまた、ハーバード大学 (2002 年 10 月から 12 月) および他のいくつかの有名な機関で訪問研究を行いました。 数論の分野における傑出した貢献により、2002 年にホワイトヘッド賞、2008 年にシニア バーウィック賞を受賞しました。 2017 年、Buzzard は、数学研究におけるコンピューター支援証明ツールの使用促進に特化した、リーン定理証明者に関するプロジェクトとブログを立ち上げました。 彼はまた、ミュージシャンのダン・スナイス (芸名カリブー) の超収束シーゲルモジュールシンボルの研究に関する数学博士論文を指導し、スナイスはこの論文でインペリアル・カレッジ・ロンドンから博士号を取得しました。 2023 年 10 月、Kevin Buzzard はソーシャル メディアで、研究資金を受け取り、フェルマーの最終定理を証明するためにリーンを使用し始めたと述べました。 「10年前なら、これには無限の時間がかかっただろう」とバザード氏は語った。彼はプロジェクトを完了するために教職を5年間保留する予定だ。 自分の仕事を脇に置く価値はありますか? 彼の同僚である英国ノッティンガム大学のクリス ウィリアムズ氏の意見では、この種のプロジェクトは予期せぬ利益と広範囲にわたる影響をもたらす可能性があります。 「彼が今後 5 年以内に証明全体を正式に定式化する可能性は低いと思います。そうでなければ、それは驚くべきことです。しかし、数論と算術幾何学の多くのツールはどこにもありません」今日は見つかりませんが、ここにはありませんので、将来の大きな進歩が非常に役立つことを期待しています。」 このプロジェクトもさらに深い価値を明らかにします。 コンピューティング ツールの継続的な進歩に伴い、数学のさまざまな分野間の境界、さらにはさまざまな分野間の境界がますます曖昧になってきており、その結果、一部のタスクでは検証がほぼ不可能になっています。 . 証拠が出てきました。 たとえば、日本の数学者である京都大学の望月新一は 500 ページの証明を書きましたが、あまりに複雑だったため、出版するまでに数年かかりました。それをどうするか。 今後、数学の境界がますます曖昧になっていくかもしれません。 これは、真実性や論理的な曖昧さのことではなく、証明に組み込むことができるさまざまなアイデアの範囲を指します。 リーンを使用すると、数学者は自分のアイデアをコードに変換でき、同僚が理解しやすくなります。先人たちが記録した先例を参考にすれば、将来の数学者はこれに基づいて独自の研究を進め続けることができます。 バザード氏は、リーンでの数学的記述の特徴は、正確に述べられているが証明されていない結果を残すことができ、後で他の人がそれらを解決できることであると述べました。 Lean 自体がそのようなワークフローを容易にします。 言い換えれば、フェルマーの最終定理は「クラウドソーシング」を通じて解決される準備が整っているということです。特にコーディングが今後も継続される場合には、バザードの残りの勤務年数。 数学的証明を完了するには、コミュニティ全体の努力が必要です。 おそらく、将来的には、数学的証明を共有し解釈するための Genius.com のようなプラットフォームができるかもしれません。 #参考: 写真
写真 写真
写真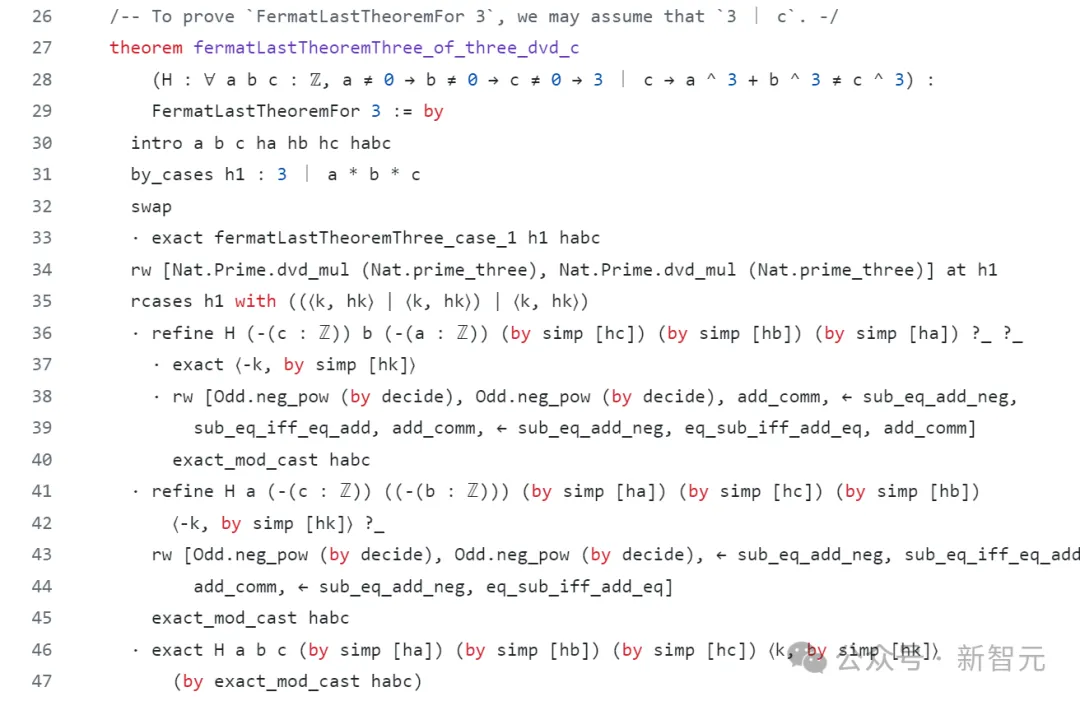 図
図
Kevin Buzzard: Lean のエバンジェリスト
 写真
写真 写真
写真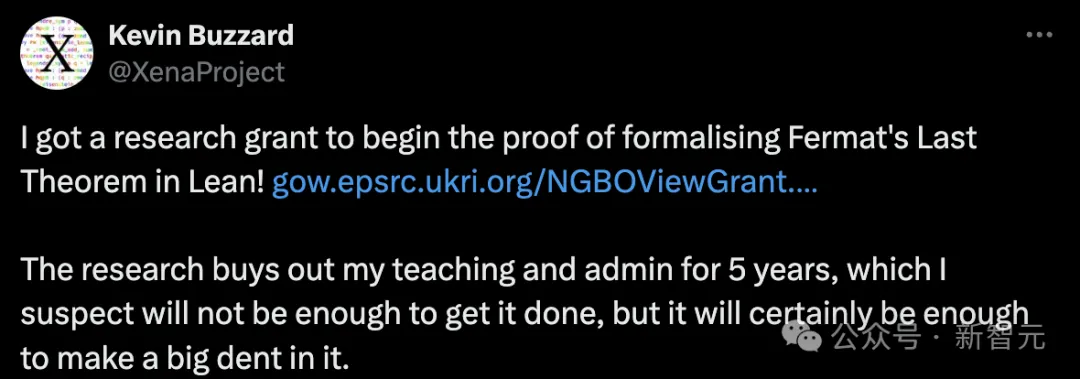 写真
写真
#数学研究にとって重要
 写真
写真
以上がAIはフェルマーの最終定理を克服できるか?数学者は100ページの証明をコードに変えるために5年間のキャリアを放棄したの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

