Bellman Ford アルゴリズムと Python での実装の詳細な説明

Bellman Ford アルゴリズム (Bellman Ford) は、重み付きグラフ内のターゲット ノードから他のノードまでの最短パスを見つけることができます。これはダイクストラ アルゴリズムに非常に似ており、ベルマン フォード アルゴリズムは負の重みを持つグラフを処理でき、実装の点では比較的単純です。

ベルマン フォード アルゴリズムの原理の詳細な説明

ベルマン フォード アルゴリズムは、開始頂点から他のすべての頂点までのパスの長さを過大評価することにより、過大評価されたパスよりも短い新しいパスを繰り返し見つけます。

各ノードのパス距離を記録したいので、それをサイズ n の配列に保存できます。n はノードの数も表します。

インスタンス図

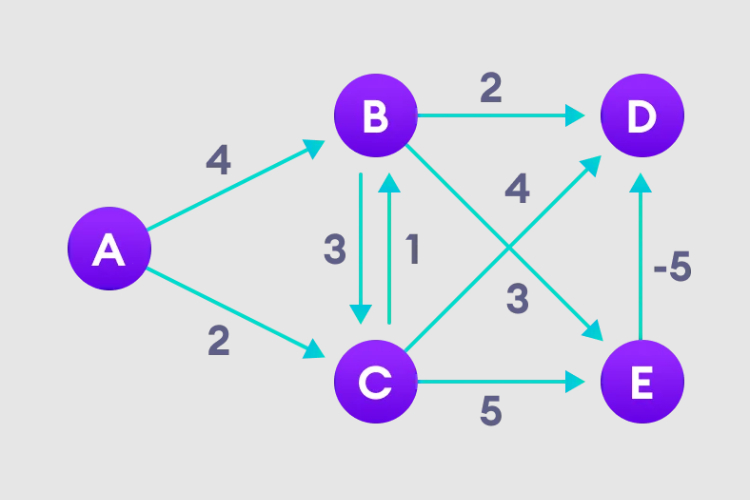
#1. 開始ノードを選択し、それを他のすべての頂点に無限に割り当て、パス値を記録します。 。

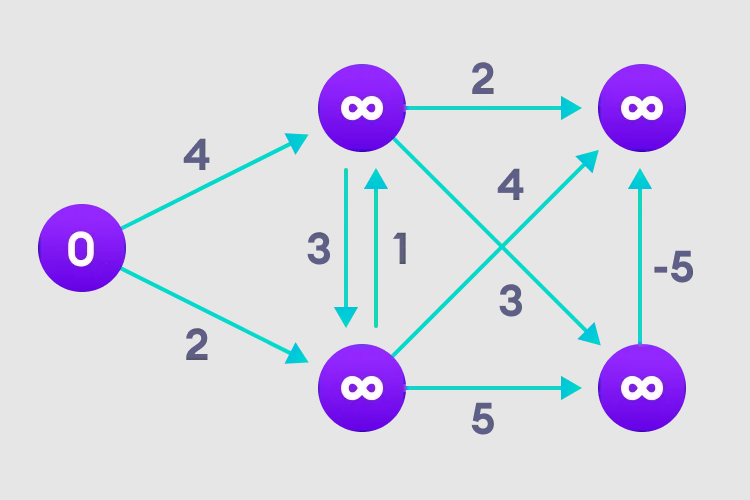
2. 各エッジを訪問し、緩和操作を実行して、最短パスを継続的に更新します。

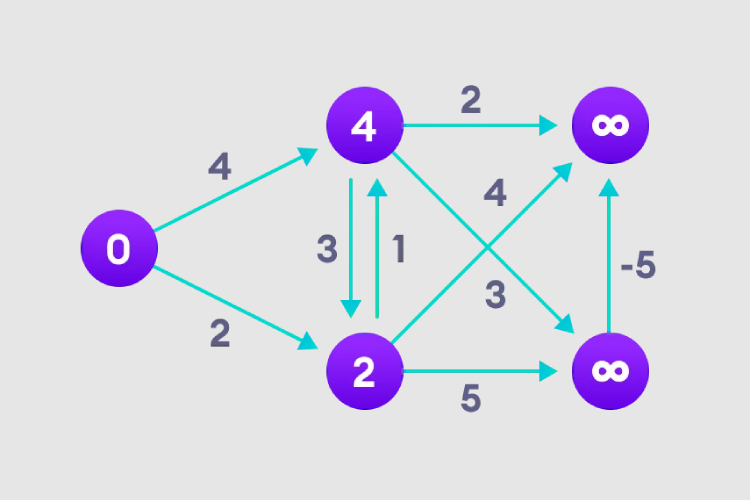
3. 最悪の場合、最短ノード パスの長さを N 回調整する必要があるため、これを N-1 回行う必要があります。 - 1回。

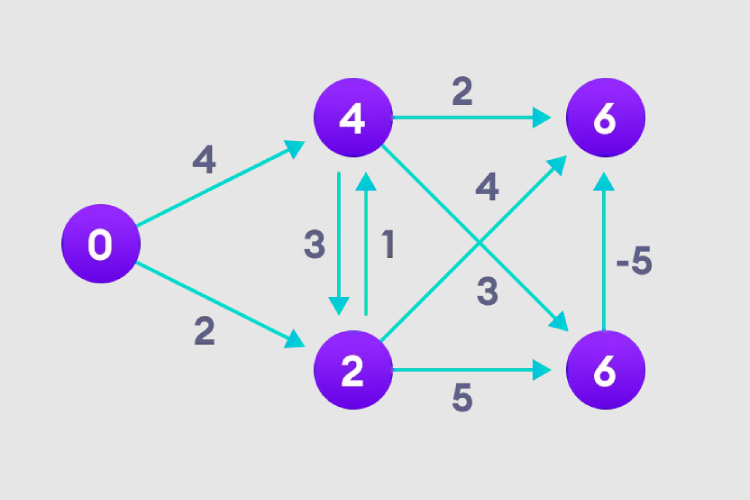
4. 右上隅のノードがパスの長さをどのように調整するかに注目してください。

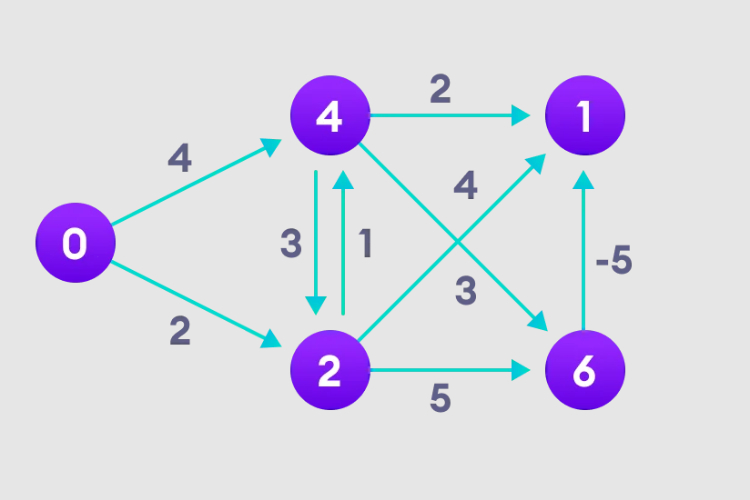
5. すべてのノードにパス長が設定されたら、負のループがあるかどうかを確認します。

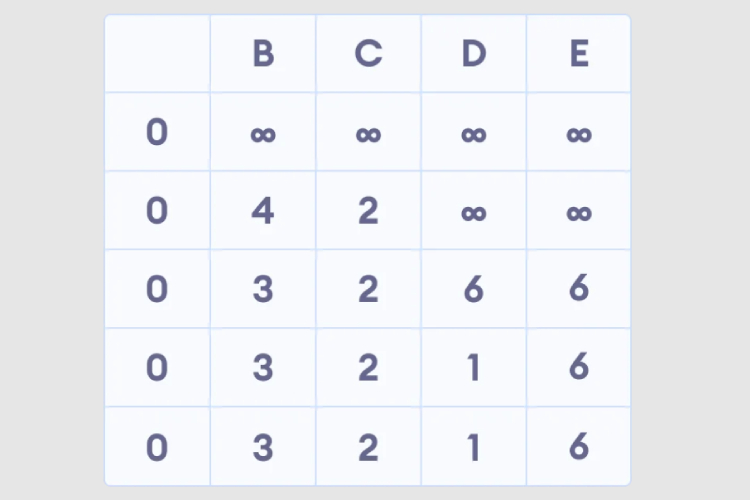Python は Bellman Ford アルゴリズムを実装します

class Graph:

    def __init__(self, vertices):
        self.V = vertices   # Total number of vertices in the graph
        self.graph = []     # Array of edges

    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    def print_solution(self, dist):
        print("Vertex Distance from Source")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

    def bellman_ford(self, src):

        dist = [float("Inf")] * self.V
        dist[src] = 0

        for _ in range(self.V - 1):
            for s, d, w in self.graph:
                if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                    dist[d] = dist[s] + w

        for s, d, w in self.graph:
            if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                print("Graph contains negative weight cycle")
                return

        self.print_solution(dist)

g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)

以上がBellman Ford アルゴリズムと Python での実装の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。