Ford-Fulkerson アルゴリズムを解析し、Python を介して実装する

Ford-Fulkerson アルゴリズムは、ネットワーク内の最大フローを計算するために使用される貪欲なアルゴリズムです。原則として、正の残存容量を持つ増強パスを見つけることです。増強パスが見つかる限り、パスの追加とトラフィックの計算を続行できます。増加経路が存在しなくなるまで、最大流量を得ることができます。

Ford-Fulkerson アルゴリズムの用語

残り容量: 容量から流量を差し引いた値です。Ford-Fulkerson アルゴリズムでは、使用を継続できるようになるまでの残り容量は正の数になります。パスとして。

残余ネットワーク: 残余容量を容量として使用する、同じ頂点と辺を持つネットワークです。

拡張パス: これは、残差グラフ内のソース ポイントから受信ポイントまでのパスであり、最終容量は 0 です。

Ford-Fulkerson アルゴリズムの原理の例

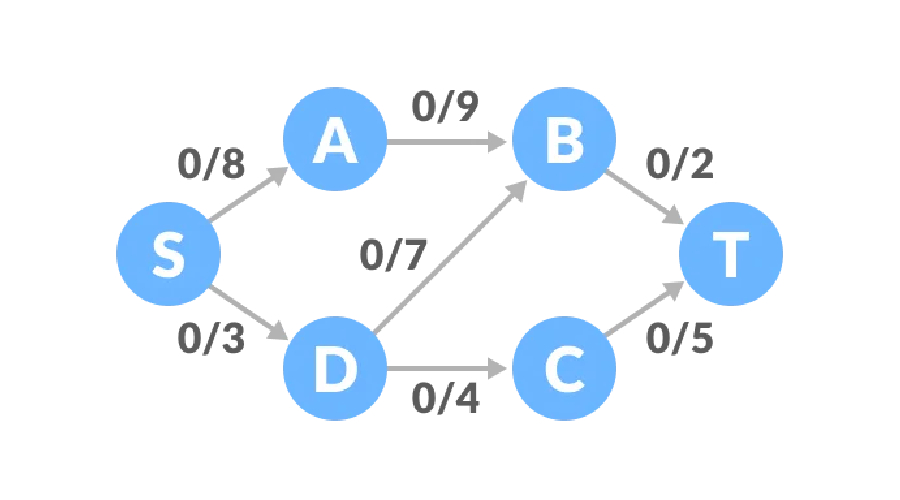
概念はあまり明確ではないかもしれません。例を見てみましょう。フロー ネットワークのすべてのエッジの初期トラフィックは 0 で、対応するトラフィックがあります。容量上限を設定します。開始点を S、受信点を T とします。

パス 1、S-A-B-T パスの残りの容量は 8、9、2、最小値は 2 であるため、パスのトラフィックは1 つは 2 です。この時点で、ネットワーク図の流量は 2 になります。

パス 2、S-D-C-T パスの残りの容量は 3、4、5、最小値は 3 であるため、容量を増やすことができます。この時点でネットワークのトラフィックは 5 になります。

パス 3、S-A-B-D-C-T パスの残りの容量は 6、7、7、1、2 で、最小値は 1 です。トラフィックは 1 増加し、この時点のネットワーク トラフィックは 6 になります。

#この時点では、正の残存容量はなく、フロー ネットワークの最大フローは 6 です。

Python は Ford-Fulkerson アルゴリズムを実装します

from collections import defaultdict

class Graph:

    def __init__(self, graph):
        self.graph = graph
        self. ROW = len(graph)

    def searching_algo_BFS(self, s, t, parent):

        visited = [False] * (self.ROW)
        queue = []

        queue.append(s)
        visited[s] = True

        while queue:

            u = queue.pop(0)

            for ind, val in enumerate(self.graph[u]):
                if visited[ind] == False and val > 0:
                    queue.append(ind)
                    visited[ind] = True
                    parent[ind] = u

        return True if visited[t] else False

    def ford_fulkerson(self, source, sink):
        parent = [-1] * (self.ROW)
        max_flow = 0

        while self.searching_algo_BFS(source, sink, parent):

            path_flow = float("Inf")
            s = sink
            while(s != source):
                path_flow = min(path_flow, self.graph[parent[s]][s])
                s = parent[s]

            max_flow += path_flow

            v = sink
            while(v != source):
                u = parent[v]
                self.graph[u][v] -= path_flow
                self.graph[v][u] += path_flow
                v = parent[v]

        return max_flow

graph = [[0, 8, 0, 0, 3, 0],
         [0, 0, 9, 0, 0, 0],
         [0, 0, 0, 0, 7, 2],
         [0, 0, 0, 0, 0, 5],
         [0, 0, 7, 4, 0, 0],
         [0, 0, 0, 0, 0, 0]]

g = Graph(graph)

source = 0
sink = 5

print("Max Flow: %d " % g.ford_fulkerson(source, sink))

以上がFord-Fulkerson アルゴリズムを解析し、Python を介して実装するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。